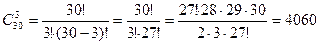Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 5. Основы теории вероятностей и математической статистики.Содержание книги
Поиск на нашем сайте
В результате изучения раздела студент должен: знать: ¾ основные понятия комбинаторики; ¾ классическое определение вероятности; ¾ определение случайной величины; ¾ математические характеристики случайной величины: математическое ожидание и дисперсию; уметь: ¾ решать задачи на нахождение вероятности события; ¾ решать задачи на нахождение математического ожидания и дисперсии случайной величины. Основные понятия комбинаторики В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, …, 9 и составлять из них комбинации, то будем получать различные числа, например, 345, 534, 1036, 5671, 45 и т.п. Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (345 и 534), другие – входящими в них цифрами (1036, 5671), третьи различаются и числом цифр (345 и 45). Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: размещения, перестановки и сочетания. Однако предварительно познакомимся с понятием факториала. Произведение всех натуральных чисел от 1 до n включительно называют n – факториалом.
1. (1.1), Пример. Сколько двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5 при условии, что ни одна из них не повторяется? Решение. Так как двузначные числа отличаются друг от друга или самими цифрами, или их порядком, то искомое количество равно числу размещений из пяти элементов по два:
Ответ: 20. Задание. Сколькими способами из восьми кандидатов можно выбрать три лица на три должности? Решение. __________________________________________________________________________________________________________________________________________________________ Ответ: 336. 2. Перестановки. Перестановками из n элементов называются такие соединения из всех n элементов, которые отличаются друг от друга порядком расположения элементов.
Пример. Пусть даны три буквы А, В, С. Сколько можно составить комбинаций из этих букв? Решение. Число перестановок из трех элементов можно вычислить по формуле: 3! = Ответ: 6. Задание. Сколькими способами можно рассадить 7 человек по 7 местам? Решение. __________________________________________________________________________________________________________________________________________________________ Ответ: 5040. 3. (1.3) Пример. Сколькими способами можно выбрать трех дежурных, если в классе 30 учащихся? Решение. Так как из 30 учащихся нужно выбрать 3, то можно составить комбинации, отличающиеся друг от друга хотя бы одним элементом, т.е. сочетания из 30 по 3:
Ответ: 4060. Задание. Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой? Решение. ______________________________________________________________________________________________________________________________________________________ Ответ: 3003. Вопросы для самоконтроля 1. Перечислите основные задачи комбинаторики. 2. Что называется перестановками? 3. Запишите формулу для перестановок из n элементов. 4. Что называется размещениями? 5. Запишите формулу числа размещений из n элементов по m. 6. Что называется сочетаниями? 7. Запишите формулу для числа сочетаний из n элементов по m. Контрольное задание
_____________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 942; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.113 (0.006 с.) |

 Размещения. Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Размещения. Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
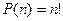 (1.2)
(1.2) = 6.
= 6.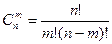 Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.