
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый и второй замечательные пределы.Стр 1 из 7Следующая ⇒
Структура рабочей тетради
¾ пояснительная записка; ¾ тематический план; ¾ рекомендации по работе с математическим текстом; ¾ рекомендации по конспектированию; ¾ рекомендации по решению задач.
¾ основные требования к математической подготовке студентов; ¾ теоретический материал; ¾ примеры решения типовых задач; ¾ задания для самостоятельного выполнения; ¾ вопросы для самоконтроля; ¾ контрольные задания.
1. Введение Пояснительная записка Настоящая Рабочая тетрадь (РТ) разработана на основе Государственного образовательного стандарта СПО, базисного плана по специальности и примерной программы по математике, утвержденной ИПР СПО. Учебная дисциплина «Математика» является компонентом инвариантной части учебного плана любой специальности и изучается на третьем курсе НТМТ (ФСПО) на базе среднего (полного) общего образования. Национально-региональный компонент введен с учетом региональной специфики содержания образования в следующих аспектах: ¾ взаимодействие с базовым предприятием ОАО «Научно-производственная корпорация «Уралвагонзавод»; ¾ историческое развитие различных отраслей народного хозяйства Горнозаводского управленческого округа. Изучение курса математики позволяет сформировать базовые математические понятия, используемые при изучении специальных дисциплин, общеучебные и специальные умения и навыки, а также общекультурные компетенции. Разработка и внедрение в педагогическую практику более совершенной методики обучения, обеспечивающей повышение качества, активизацию познавательной деятельности студентов и развитие их умственных способностей, является важнейшей проблемой. В ее решении значительная роль отводится формированию умений и навыков самостоятельного мышления и практического применения знаний. Немаловажным является и формирование навыков самостоятельного умственного труда. Это тем более важно, что какие бы знания и в каком объеме не получали наши обучаемые, эти знания имеют необратимую тенденцию быстро устаревать, отставать от потребностей жизни и производства. Поэтому нужно научиться самостоятельно приобретать знания из различных источников информации самостоятельным путем, овладевать как можно большим разнообразием видов самостоятельной работы, в чём поможет работа с РТ.
. Основная цель данной Рабочей тетради – познакомить Вас с содержанием курса математики, основной задачей которого является математическое обеспечение специальной подготовкой, то есть вооружение студентов математическими знаниями и умениями, необходимыми для изучения специальных дисциплин, разработки курсовых и дипломных проектов, для профессиональной деятельности и необходимых для повседневной жизни, формирование описания о методе познания действительности, формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса. Тематический план
Рекомендации по работе с математическим текстом
Любой математический текст является сложным, так как содержит определенное количество научных терминов, изученных ранее или новых. В нем также присутствуют формулы, их выводы, доказательства утверждений и теорем, что является наиболее затруднительным в восприятии. Начиная самостоятельно изучать материал какого-либо математического текста, необходимо прочитать весь текст, не задерживаясь на трудном материале. При повторном чтении следует обдумывать смысл каждой фразы. Затем необходимо составить план конспекта. Вывод формул, определения, формулировки и доказательства теорем записывать в тетрадь. Изучение закончить повторением материала, приводя примеры и объясняя их. Материал можно считать усвоенным, если при его повторении не возникает необходимость заглянуть в РТ или конспект. Если при изучении теоретического материала обучаемый встречает затруднения, которые он не может устранить самостоятельно, повторно изучая основную и дополнительную литературу, необходимо обратитьсяк преподавателю для получения устной или письменной консультации. Рекомендации по конспектированию Конспект — сложная запись содержания исходного текста, включающая в себя заимствования (цитаты, формулы, определения) наиболее примечательных мест в соответствии с планом источника, а также сжатый анализ записанного материала и выводы по нему. Общий порядок работы над конспектом: ¾ определение структуры конспектируемого материала, при этом очень помогает составление плана по ходу изучения текста; ¾ отбор и последующая запись наиболее существенного содержания текста в форме цитат, доказательств или близкого изложения без потерь смысла; ¾ анализ записей и на его основе дополнение наиболее сложных элементов текста; ¾ комментарии (располагать их можно на полях или в виде сносок); ¾ завершение формулирования и запись выводов по каждой из частей текста, а также общих выводов в заключении.
Рекомендации по решению задач Хорошее усвоение теоретического материала невозможно без решения задач. Многочисленные формулы запомнить трудно, в процессе же решения задач они запоминаются легче. Поэтому в каждой теме содержатся задачи и упражнения, рекомендованные для самостоятельного решения. Темы и задания, отмеченные * - повышенной трудности, выполняются по желанию студента. Приступая к решению задачи, необходимо внимательно прочесть условие и, уяснив смысл, записать кратко, используя математические символы, условие и искомые результаты. Затем записать необходимые формулы и приступить к решению. Результатом работы является Рабочая тетрадь с выполненными заданиями для самостоятельной работы, контрольными заданиями, которая сдается на проверку в электронном или печатном варианте. Раздел 1. Теория пределов В результате изучения раздела студент должен знать: ¾ определение предела функции в точке; ¾ свойства предела функции в точке; ¾ формулы замечательных пределов; ¾ определение непрерывности функции в точке,
¾ свойства непрерывных функций;
уметь: ¾ вычислять пределы функций в точке и на бесконечности.
Предел последовательности Определение предела последовательности Определение. Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число ап, то говорят, что задана числовая последовательность
Определение. Число А называется пределом последовательности (аn), если для каждого положительного числа e найдется такое натуральное число N, что для любого n > N справедливо неравенство: Определение. Последовательность (an), имеющая предел А, называется сходящейся к числу А, не имеющая предела последовательность называется расходящейся.
Таким образом, все члены последовательности (an), сходящейся к числу А, имеющие порядковые номера Величина 1) оставаясь меньше своего предела, 2) оставаясь больше своего предела, 3) колеблясь около своего предела и 4) принимая значения, равные своему пределу. Пример. Докажем, что последовательность с общим членом Решение.Выберем произвольно положительное число ε и покажем, что для него можно определить такое натуральное число N, что для всех номеров п > N будет выполняться неравенство, рассмотренное выше, в котором надо взять А = 1, т. е. неравенство
После приведения в скобках к общему знаменателю получим
Но если Из последнего неравенства следует, что Значит, если номер N больше, чем Теперь надо решить вопрос о числе N, о котором идет речь в определении. За число N можно принять наибольшее целое число, содержащееся в числе
Таким образом, попроизвольно заданному положительному числу Проиллюстрируем это числовым примером. Пусть, например, Таким образом, для членов последовательности с номером большим, чем 99, выполняется неравенство: Пусть п = 97; тогда, так как если п = 98, то Из этих расчетов видно, что когда номер п члена последовательности меньше 99 неравенство если п = 98, то Полученный результат можно записать так: Мы употребили запись Символ Очевидно, что последовательность
Пример. Докажем, что последовательность 3, З2, 33,34,..., 3 "... не имеет предела. Решение. Мы докажем требуемое, если установим, что общий член этой последовательности Пусть А такое число. Возьмем  и подавно и подавно  , или 3 п > А. Тем самым показано, что 3 п может превзойти любое число А. Если бы существовал предел переменной , или 3 п > А. Тем самым показано, что 3 п может превзойти любое число А. Если бы существовал предел переменной  , и был бы равен А, то для любого , и был бы равен А, то для любого 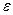 > 0 можно было бы подобрать такое N, что при номерах п > N выполнялись бы неравенства a > 0 можно было бы подобрать такое N, что при номерах п > N выполнялись бы неравенства a  , т. е. , т. е.  , а это противоречит доказанному, так как 3 п при , а это противоречит доказанному, так как 3 п при  превзойдет любое число А, а тем самым и число a + превзойдет любое число А, а тем самым и число a + 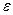 , меньше которого оно должно оставаться. Это противоречие и доказывает, что данная последовательность предела не имеет. Этот пример иллюстрирует утверждение: не всякая последовательность имеет предел. , меньше которого оно должно оставаться. Это противоречие и доказывает, что данная последовательность предела не имеет. Этот пример иллюстрирует утверждение: не всякая последовательность имеет предел.
Свойства пределов последовательностей Если две последовательности
1) Последовательность
Это свойство распространяется на случай любого фиксированного числа слагаемых, 2) Последовательность
Это свойство распространяется также на случай любого фиксированного числа сомножителей. Постоянный множитель можно выносить за знак предела:
при любом постоянном k. 3) Последовательность
при условии, что все уп не равны нулю и
Пример. Найдем предел последовательности: Решение. Очевидно, что числитель и знаменатель данной дроби имеют бесконечные пределы, т. е. представляют собой расходящиеся последовательности. Для разрешения проблемы произведем тождественное преобразование дроби, почленно разделив ее на наибольшую из степеней п (в данном случае, на
Здесь применена теорема о пределе дроби. Ответ:–2. Пример. Найдем 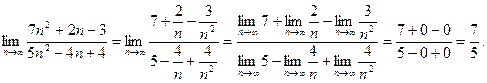
Ответ: Задание. Вычислите предел последовательности:
Решение: __________________________________________________________________________________________________________________________________________________________
Ответ: Предел функции Определение предела функции в точке Сформулируем определение предела функции в точке. Определение. Пусть функция f(x) определена в некоторой окрестности точки а, кроме, может быть, самой точки а, Число В называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хп ¹ а, п Î N, сходящейся к а, последовательность соответствующих значений функции f(xп), п Î N, сходится к числу В. В этом случае пишут: Если же для некоторой последовательности значений аргумента, сходящейся к а, соответствующая последовательность значений функции не является сходящейся, то функция в данной точке не имеет предела. То же заключение можно сделать, если для двух различных последовательностей значений аргумента последовательности соответствующих значений функции имеют различные пределы. Очевидно, число В является пределом функции
Отметим, что точка а, в которой рассматривается предел функции
Пример. Докажем справедливость следующих равенств: 1) Решение. 1) Пусть Следовательно 2) Для любой последовательности (хn) такой, что хn ® а при n ® ¥, имеем
Следовательно, согласно определению предела
Свойства пределов функций Основные свойства пределов функций аналогичны теоремам о пределах числовых последовательностей:
1) Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: 2) Предел произведения функций равен произведению их пределов, если последние существуют: Следствие. Постоянный множитель можно выносить за знак предела: 3) Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: При изучении пределов функций иногда полезно использовать следующую «теорему о пределе промежуточной функции». Теорема. Если Пример. Вычислите пределы фукций: 1) Решение. 1) 2) Поскольку предел знаменателя равен 0, то воспользоваться теоремой о пределе частного невозможно. Поэтому первоначально сократим дробь, разложив числитель на множители:
3) 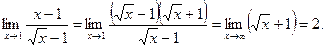
Ответ. 1) 11, 2) –1, 3) 2.
Задание. Вычислите пределы функций: 1). Решение: ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Ответ:-1 2). Решение: ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ:-6.
Определение предела функции на бесконечности При изучении свойств функции приходится рассматривать предел функции в бесконечности, бесконечный предел функции в точке, а также бесконечный предел в бесконечности. Рассмотрим более подробно предел функции в бесконечности, т.е. при Определение. Пусть функция f(x) определена на всей числовой прямой. Число В называется пределом f(x) при В этих случаях пишут, что Пример. Докажем, что Решение. Рассмотрим произвольную последовательность (хп) такую, что
Так как последовательность
Кроме рассмотренного случая конечного предела функции f(x) при х ® ∞ (или иначе х ® ± ¥) используется понятие бесконечного предела. Например, функция Определение. Если для любой последовательности значений аргумента (хп) такой, что хп ¹ 0 и Пример. Найдите пределы функций: 1) Решение. При определении значений предела функции на бесконечности воспользуемся тем же приемом, что и в случае последовательности: 1) 2) 
Ответ. 1) -3, 2) 0.
Задание. Вычислите предел функции на бесконечности:
Решение: ____________________________________________________________________________________________________________________________________
Ответ:-1.
Непрерывность функции Пример. Функция f(x) = x2 определена на всей числовой прямой и непрерывна в точке х = 1 поскольку f( 1 ) = 1 и
Непрерывность функции на множестве Определение. Функция f(x), называется непрерывной на интервале (a; b), если она непрерывна в каждой точке этого интервала. Если функция непрерывна в некоторой точке, то эта точка называется точкой непрерывности данной функции. В тех случаях, когда предел функции в данной точке не существует или его значение не совпадает со значением функции в данной точке, то функция называется разрывной в этой точке, а сама точка – точкой разрыва функции f(x). Свойства непрерывных функций. 1) Сумма конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке. 2) Произведение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке. 3) Отношение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точке а. Пример. 1) Функция f(x) = xп, где n Î N, непрерывна на всей числовой прямой. Доказать этот факт можно, используя свойство 2 и непрерывность функции f(x) = x. 2) Функция f(x) = сxп (с – константа) непрерывна на всей числовой прямой, исходя из свойства 2 и примера 1. Теорема 2. Любая дробно-рациональная функция непрерывна в каждой точке своей области определения. Пример. 1) Функция 2)  непрерывна всюду на R, т.к. знаменатель нигде не обращается в нуль. непрерывна всюду на R, т.к. знаменатель нигде не обращается в нуль.
Определение Функция f(x) называется непрерывной в точке х = а, если в этой точке ее приращение
Односторонние пределы функции* Левосторонний предел функции. Если отыскивается предел функции f(x) при условии, что х, стремясь к а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним пределом функции f (х) (или левым пределом функции). Для того чтобы показать, что х стремится к а, оставаясь меньше а, употребляется запись: Правосторонний предел функции. Если отыскивается предел функции f(x) при условии, что х, стремясь к а, может принимать только такие значения, которые больше а, то этот предел, если он существует, называется правосторонним пределом функции f(x) (или правым пределом функции). То, что х, стремясь к а, остается больше а, обозначается так: Очевидно, что предел функции при Определение Функция f(x) называется непрерывной при х = а, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т. е. f(a). То есть:
Точки разрыва и их классификация* Если равенство Точка разрыва первого рода
Точка разрыва второго рода
Устранимый разрыв Определение. Если в точке х = а функция f(x) имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке а, т. е. со значением f(a), то точка х = а называется точкой устранимого» разрыва. Таким образом, в этом случае
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.217.228 (0.156 с.) |

 . Числа а1, а2,…,ап называются членами последовательности, а число ап – общим или п – м членом последовательности.
Определение. Последовательность (an) называется ограниченной, если существуют числа M и m такие, что для любого n выполняется неравенство: m £ (an) £ M. В противном случае она называется неограниченной.
. Числа а1, а2,…,ап называются членами последовательности, а число ап – общим или п – м членом последовательности.
Определение. Последовательность (an) называется ограниченной, если существуют числа M и m такие, что для любого n выполняется неравенство: m £ (an) £ M. В противном случае она называется неограниченной.
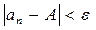 . В этом случае пишут
. В этом случае пишут 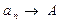 при
при  или
или 
 :
: 
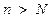 лежат в интервале (А– e; А + e), который называется e- окрестностью точки А.
лежат в интервале (А– e; А + e), который называется e- окрестностью точки А.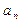 может стремиться к своему пределу различными способами:
может стремиться к своему пределу различными способами: имеет предел, равный 1.
имеет предел, равный 1.
 или
или 
 .
. , а
, а  .
. , то неравенство
, то неравенство  Итак, можно принять
Итак, можно принять 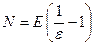 (предполагается, что
(предполагается, что  , иначе N не будет натуральным и его надо брать равным 1).
, иначе N не будет натуральным и его надо брать равным 1). . Тогда при
. Тогда при  следующее значение:
следующее значение:  или
или 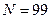

 , то
, то  , а
, а 
 и
и  , а
, а 
 Если взять номер, превышающий 99, например, п = 101, то получим
Если взять номер, превышающий 99, например, п = 101, то получим  и
и  , а
, а  .
. . Иначе можно сказать, что последовательность
. Иначе можно сказать, что последовательность  сходится к 1.
сходится к 1. , которую следует понимать так: переменная величина п становится все большей и большей и не существует предела для ее возрастания. Какое бы большое число мы ни задали, п в процессе своего возрастания его превзойдет. Для того чтобы коротко описать этот характер изменения п, принято говорить «эн стремится к бесконечности» и записывать это так:
, которую следует понимать так: переменная величина п становится все большей и большей и не существует предела для ее возрастания. Какое бы большое число мы ни задали, п в процессе своего возрастания его превзойдет. Для того чтобы коротко описать этот характер изменения п, принято говорить «эн стремится к бесконечности» и записывать это так:  произносится «бесконечность» и применяется для сокращенной записи слова «бесконечность».
произносится «бесконечность» и применяется для сокращенной записи слова «бесконечность». , так как п может равняться числу и не может быть равно символу, введенному только для сокращенной записи и сокращенного произношения фразы, которой заранее был придан определенный, указанный выше, смысл.
, так как п может равняться числу и не может быть равно символу, введенному только для сокращенной записи и сокращенного произношения фразы, которой заранее был придан определенный, указанный выше, смысл.
 превзойдет любое наперед заданное число.
превзойдет любое наперед заданное число. и
и  имеют пределы, равные соответственно А и В, то:
имеют пределы, равные соответственно А и В, то: имеет предел, равный
имеет предел, равный  :
:
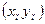 имеет предел, равный
имеет предел, равный  , т. е.
, т. е.

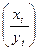 имеет предел, равный
имеет предел, равный  , т. е.
, т. е.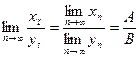 .
. .
.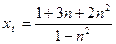 .
. ). Предел полученной дроби найдем, определив значение предела каждого слагаемого в отдельности и учитывая, что
). Предел полученной дроби найдем, определив значение предела каждого слагаемого в отдельности и учитывая, что  при условии, что с и k – постоянные, причем k больше 1. Помните, что предел постоянной величины есть сама величина, поскольку последовательность, все члены которой равны, имеет предел, равный ее общему члену. После этих подробных рассуждений укажем, как следует расположить записи:
при условии, что с и k – постоянные, причем k больше 1. Помните, что предел постоянной величины есть сама величина, поскольку последовательность, все члены которой равны, имеет предел, равный ее общему члену. После этих подробных рассуждений укажем, как следует расположить записи: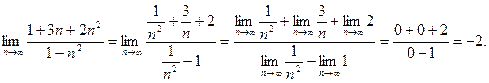
 .
.


 или
или  при
при  .
. при
при 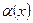 , где
, где  при
при  , при
, при  при
при  .
. = с и
= с и  .
. .
.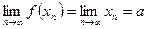 .
. .
. .
. .
. , если
, если  существует.
существует. , если
, если  .
. ,
, 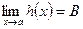 и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства
и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства  , то
, то  ; 2)
; 2)  ; 3)
; 3) 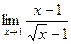 .
.



 и при
и при 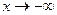 .
. , если
, если  для любой последовательности (хп) такой, что
для любой последовательности (хп) такой, что 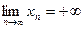 .
. . Аналогично,
. Аналогично,  ,если
,если  для любой последовательности (хп) такой, что
для любой последовательности (хп) такой, что  .
.
 , где n Î N, сходится к 1, то согласно определению
, где n Î N, сходится к 1, то согласно определению  .
. , определенная для всех х ¹ 0, принимает сколь угодно большие значения при х ® 0. В этом случае говорят, что функция в точке х = 0 имеет своим пределом бесконечность, и пишут
, определенная для всех х ¹ 0, принимает сколь угодно большие значения при х ® 0. В этом случае говорят, что функция в точке х = 0 имеет своим пределом бесконечность, и пишут  .
. , имеет место
, имеет место 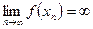 , то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут
, то говорят, что предел функции f(x) в точке а есть бесконечность, и пишут  .
. ; 2)
; 2) 

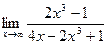

 непрерывна на всей числовой прямой, кроме точки
непрерывна на всей числовой прямой, кроме точки  , в которой знаменатель дроби обращается в нуль.
, в которой знаменатель дроби обращается в нуль. стремится к нулю, когда приращение аргумента
стремится к нулю, когда приращение аргумента  стремится к нулю, или иначе: функция f (х) называется непрерывной в точке х = а, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если
стремится к нулю, или иначе: функция f (х) называется непрерывной в точке х = а, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если 
 , а левосторонний предел функции обозначается символом:
, а левосторонний предел функции обозначается символом: 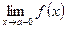 .
. , а правосторонний предел функции обозначается символом:
, а правосторонний предел функции обозначается символом:  .
.
 .
.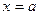 говорят, что она является точкой разрыва.
говорят, что она является точкой разрыва. Рис. 2
Рис. 2

 то точка а называется точкой разрыва первого рода (см. рис. 2).
то точка а называется точкой разрыва первого рода (см. рис. 2).
 а) б)
а) б)

 . Разрыв «устраняется» тем, что полагают
. Разрыв «устраняется» тем, что полагают  .
.


