
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 3. Интегральное исчисление функции одной переменнойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В результате изучения раздела студент должен: знать: ¾ определение первообразной; ¾ определение неопределенного интеграла и его свойства; формулы интегрирования; ¾ способы вычисления неопределенного интеграла; ¾ определение определенного интеграла, его геометрический смысл и свойства; ¾ способы вычисления определенного интеграла; ¾ понятие криволинейной трапеции, способы вычисления площадей криволинейных трапеций с помощью определенного интеграла; уметь: ¾ находить неопределенные интегралы, сводящиеся к табличным с помощью основных свойств и простейших преобразований; ¾ выделять первообразную, удовлетворяющую заданным начальным условиям; ¾ вычислять определенный интеграл с помощью основных свойств и формулы Ньютона-Лейбница; ¾ находить площади криволинейных трапеций.
Первообразная функции. Неопределенный интеграл и его свойства. Таблица интегралов.  . .
Свойство первообразной. Если F1(x) и F2(x) – первообразные для функции f(x) в некотором промежутке Х, то найдется такое число С, что справедливо равенство: Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается Согласно определению, Свойства неопределенного интеграла.
Таблица интегралов:
Приемы интегрирования Метод непосредственного интегрирования Метод интегрирования, основанный на применении четвертого и пятого свойств неопределенного интеграла, называется методом разложения или методом непосредственного интегрирования. Пример. Найдем: 1) 3) Решение. 1)Представим интеграл в виде суммы интегралов и, произведя вынесение коэффициентов за знак интеграла, сведем их к табличным:
2) Возведя в квадрат подынтегральное выражение, повторим операцию, рассмотренную в предыдущем примере:
3) Произведя почленное деление подынтегрального выражения на х3, получим:
Задание. Найти: 1) _____________________________________________________________________________ Ответ: х2 + С 2) _____________________________________________________________________________ Ответ: Метод замены переменной Один из основных методов интегрирования – метод замены переменной (или метод подстановки), описывается следующей формулой:
Однако, новую переменную можно не выписывать явно (в таких случаях говорят о преобразовании функции под знаком дифференциала или о введении постоянных и переменных под знак дифференциала) на основании теоремы: Теорема. Пусть F(x) – некоторая первообразная для функции f(x). Тогда Пример. Найдем 1) Решение. 1)
 . Тогда . Тогда 
Произведя подстановку, получим:
2) Так как аргумент подынтегральной функции имеет вид
Задание. Найти Решение. ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Ответ: Интегрирование по частям* Формула Пример. Найдем Решение. Применим метод интегрирования по частям. Положим, что Подставляя выражения в вышеуказанную формулу, получим:
Задание*. Найти _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Ответ: Вопросы для самоконтроля 1. Какая функция называется первообразной для заданной функции? 2. Если F(x) – первообразная для f(x), то каким равенством связаны они между собой? 3. Как записать всю совокупность первообразных? 4. Что называется неопределенным интегралом? 5. В чем заключается правило интегрирования выражения, содержащего постоянный множитель? 6. В чем заключается правило интегрирования алгебраической суммы функций? 7. Как проверить результат интегрирования? 8. Какие вы знаете способы интегрирования и в чем они заключаются?
Контрольное задание Найти интегралы: __________________________________________________________________________
____________________________________________________________________________________________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________
4*. _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Определенный интеграл Пусть предел интегральной суммы при стремлении
Свойства определенного интеграла: 1. Постоянный множитель можно выносить за знак интеграла:
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: 3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.
4. Если на отрезке [a; b] f(x) £ g(x), то и 5. Если функция у = f(x) непрерывна на отрезке [a; b], то найдется такое значение x Î [a; b], что
Формула Ньютона-Лейбница. Пусть функция у = f(x) непрерывна на отрезке [a; b] и F(x) первообразная функцией для функции f(x) на отрезке [a; b]. Тогда определенный интеграл от функции f(x) на [a; b] равен приращению первообразной на этом отрезке, т.е. Пример. Вычислим следующие интегралы: 1) Решение. Эти задачи на непосредственное применение формулы Ньютона – Лейбница: 1) 2) Задание. Вычислить Решение. __________________________________________________________________________________________________________________________________________________________ Ответ: 3. Задание. Вычислить Решение. __________________________________________________________________________________________________________________________________________________________ Ответ: e - 1.
Метод замены переменной в определенном интеграле. Пусть функция Данная формула называется формулой замены переменной в определенном интеграле. Как видите, использование введения новой переменной в определенном интеграле производится аналогично тому, как это производилось в неопределенном интеграле. Однако в этом случае нет необходимости возвращаться к исходной переменной. Достаточно рассчитать и подставить новые пределы интегрирования. Пример. Вычислим Решение. Положим
Задание. Вычислить Решение. __________________________________________________________________________________________________________________________________________________________ Ответ: Метод интегрирования по частям в определенном интеграле* Пусть функции Пример. Вычислим Решение. Пусть Тогда

Вы заметили, что при расчете
Задание *. Вычислить Решение. __________________________________________________________________________________________________________________________________________________________ Ответ: 8ln4 – 4 -
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.83 (0.01 с.) |

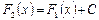 .
. .
. .
.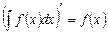 .
. .
.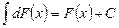 .
. .
. .
.  ;
;  (при п ¹ –1);
(при п ¹ –1);  ;
; (при а > 0, a ¹ 0);
(при а > 0, a ¹ 0); ;
; 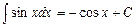 ;
; 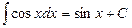 ;
; (при
(при  );
); (при a ¹ 0);
(при a ¹ 0);
 ;
;
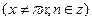 ;
; (при a ¹ 0);
(при a ¹ 0);  .
. , 2)
, 2)  ,
, .
.






 - 3sinx + С
- 3sinx + С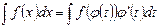 .
. , где k и b – некоторые числа, причем k ¹ 0.
, где k и b – некоторые числа, причем k ¹ 0. , 2)
, 2) 

 , где
, где  , то, применяя вышеназванную теорему, получим:
, то, применяя вышеназванную теорему, получим:


 называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подынтегрального выражения искомого интеграла на два множителя и и dv. При переходе к правой части первый их этих множителей дифференцируется, а второй интегрируется.
называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подынтегрального выражения искомого интеграла на два множителя и и dv. При переходе к правой части первый их этих множителей дифференцируется, а второй интегрируется. .
. . Тогда
. Тогда 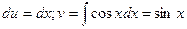 .
.






 к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек x1, x2,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается
к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек x1, x2,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается  , а сама функция у = f(x) называется интегрируемой на [a; b], т.е.
, а сама функция у = f(x) называется интегрируемой на [a; b], т.е. .
. .
.


 .
. .
. .
. .
. ; 2)
; 2)  .
. ;
;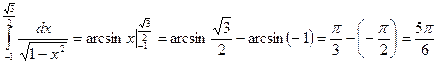


 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке  ,
,  ,
,  и функция
и функция  непрерывна в каждой точке вида
непрерывна в каждой точке вида  , где
, где  . Тогда справедливо следующее равенство:
. Тогда справедливо следующее равенство: 
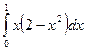 .
. . Тогда
. Тогда  . Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов:
. Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов:  ,
,  . Воспользовавшись формулой замены переменной в определенном интеграле, получим:
. Воспользовавшись формулой замены переменной в определенном интеграле, получим: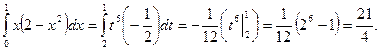

 - 1.
- 1. имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  . Тогда
. Тогда  . Эта формула называется формулой интегрирования по частям в определенном интеграле.
. Эта формула называется формулой интегрирования по частям в определенном интеграле. .
. ,
, 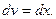
 и
и  . Воспользовавшись формулой интегрирования по частям в определенном интеграле, получим:
. Воспользовавшись формулой интегрирования по частям в определенном интеграле, получим:
 была введена переменная
была введена переменная  .
.
 .
.


