
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование сезонной составляющей при помощи фиктивных переменных.Содержание книги
Поиск на нашем сайте
На примере: Требуется составить спецификацию модели, которая позволяет объяснять величину спроса (yd) на конкурентном рынке нормального товара значением его цены (p), уровнем душевого дохода потребителя (x) и фактором сезонности (кварталом года). Этот приём заключается в использовании в модели фиктивных экзогенных переменных. В модели, обсуждаемов в данной задаче, влияние фактора сезонности на уровень спроса отразим путем включения в линейную функцию спроса трёх фиктивных переменных d1, d2, и d3. Эти переменные прнимают, по нашей договорённости, а не объективно (отсюда и происходит их название – фиктивные), следующие значения: d1={1- для первого квартала, 0- для других кварталов}; d2={1- для второго квартала, 0 - для других кварталов}; (1) d3={1- для третьего квартала, 0 - для других кварталов}. Теперь, учитывая решение задачи 1, получаем yd = a0 + a1 · p + a2 · x + b1∙d1 + b2∙d2 + b3∙d3, (2) a1 < 0, a2 >0. Это и есть модель уровня спроса на нормальное благо с учётом фактора сезонности. Заметим, что структурная форма данной модели совпадает с приведённой формой; так бывает в тех случаях, когда эконометрическая модель имеет вид изолированного уравнения. Подчеркнём, что эндогенная переменная модели (2), yd объясняется пятью экзогенными переменными, из которых три – фиктивные. Добавим, что бинарный характер (1 или 0) фиктивных переменных (1) фактически влечёт изменение структуры уравнения модели (2) в зависимости от значений этих переменных. Так, при q1=1 (первый квартал) модель спроса (2) принимает вид yd = (a0 + b1) + a1 · p + a2 · x (3) a1 < 0, a2 >0; а, скажем, в ситуации четвёртого квартала, когда q1= q2 = q3 = 0, модель (2) выглядит иначе: yd = a0 + a1 · p + a2 · x, (4) a1 < 0, a2 >0. В силу данного обстоятельства модели вида (2) с бинарными фиктивными переменными называются моделями с переменной структурой. Добавим, что состояние фактора, при котором все фиктивные переменные равны 0 именуется базовым.
Регрессионная зависимость случайных переменных. Функция регрессии, стандартные модели функции регрессии. Модели, в состав которых входят случайные возмущения, отражающие воздействие на эндогенные переменные неидентифицируемых факторов принято называть эконометрическими (регрессионными). Включение в модели случайных возмущений – есть 4-ый принцип их спецификации. Понятие ожидаемого значения случайной переменной позволяет дать точное определение понятия функции регрессии. Пусть случайная переменная y принимает свои значения в опыте вместе с переменной x (случайной или детерминированной - неважно). Обозначим символом Определение 6.2. Функцией регрессии y на x (эта функция обозначается символом
E(y Обратим внимание, что величина y = где u – случайная переменная (остаток), такая, что Кроме того, средний квадрат разброса значений переменной y вокруг величины
На практике функция (1) чаще всего неизвестна, поэтому вместо неё используют доступные модели, такие как: линейная функция - f(x)=a0+a1∙x и парабола второго порядка - f(x)=a0+a1∙x+a2∙x2 степенная - показательная - f(x) = a0 · exp(a1 · x), функция Перла-Рида - функция Джонсона - f(x) = exp(a0 + a1 /x). ЛММР
Объясняющие переменные
19. Схема Гаусса-Маркова (на примере модели Оукена). Модель Оукена:
t=1,2,... где wt - темп прироста безработицы в году t, yt - темп роста ВВП
Пусть в рамках исследуемой модели величины связаны следующим образом:
Она называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели, или иначе – схемой Гаусса-Маркова ( где
Оценку вектора обозначим где f (·, ·) – символ процедуры. Данная процедура именуется линейной относительно вектора
Понятие статистической процедуры оценивания параметров эконометрической модели. Линейные стат. процедуры. Требования к наилучшей стат. процедуре. Пусть имеется выборка
значений переменных x и y модели
Данная выборка получена на этапе наблюдения и предназначена для оценивания параметров модели
В рамках данной модели величины (*) связаны следующей СЛАУ:
Она называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели, или иначе – схемой Гаусса-Маркова. Вот компактная запись этой схемы где
Наконец, Оценку вектора обозначим где f (·, ·) – символ процедуры. Данная процедура именуется линейной относительно вектора
Класс таких всевозможных линейных процедур оценивания по исходной выборке вектора Наилучшая процедура f* (·, ·) из выбранного класса процедур F должна генерировать оценку
21. Теорема Гаусса-Маркова – Эйткена. Вывод выражения Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4) Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
где (k+1) – количество неизвестных коэффициентов функции регрессии. Доказательство а. Нам необходимо отыскать процедуру M(X), трансформирующей вектор Из предпосылок (1), (4), а также свойств ковариации следует, что Cov( Также (11) можно представить в виде Или Теперь рассмотрим требование о минимальной дисперсии.
Тогда получим следующую задачу Решив задачу получим Подставим в(9) и получим Теперь сопоставляя (10) и (13) получим
ЧТД
22. Теорема Гаусса-Маркова – Эйткена. Вывод выражения Cov Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4) Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
где (k+1) – количество неизвестных коэффициентов функции регрессии. Доказательство в. Рассмотрим процедуру Эйткена С учетом Где M = В том случае, когда выполнены (2),(3), то
23. Теорема Гаусса-Маркова – Эйткена. Вывод свойства обобщенного метода наименьших квадратов (ОМНК), Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4) Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
Доказательство. Если вектор случайных возмущений в уравнениях наблюдений имеет произвольную ковариационную матрицу (остатки гетероскедастичны и коррелированны), то оптимальная линейная процедура оценивания параметров линейной модели множественной регрессии именуется обобщённым методом наименьших квадратов (или процедурой Эйткена) и определяется формулами:
M = Обратимся к схеме Гаусса-Маркова и перепишем её по-другому:
На время будем здесь рассматривать вектор
образуем квадратичную (сложную) функцию вектора Нас интересует ответ на вопрос: при каком же значении переменного вектора
Можно проверить, что единственным решением Подставим значение результат подстановки обозначим
В частном случае, когда
так что свойство наименьших квадратов обосновано.
24. Теорема Гаусса-Маркова – Эйткена. Вывод оценки дисперсии единицы веса, Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4) Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
где (k+1) – количество неизвестных коэффициентов функции регрессии. Перепишем схему Гаусса-Маркова в следующем виде: Рассмотрим величину
Получается, что величина
служит несмещённой оценкой константы
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 - закон распределения СП y при фиксированном значении переменной x.
- закон распределения СП y при фиксированном значении переменной x.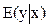 ) называется ожидаемое значение y, вычисленное при заданном значении переменной x, то есть
) называется ожидаемое значение y, вычисленное при заданном значении переменной x, то есть =
=  (1)
(1) .
. , отсюда
, отсюда .
. ,
, ,
,
 в общем случае не зависят от случайного остатка
в общем случае не зависят от случайного остатка  . Данная модель является базовой моделью эконометрики, потому что к такому виду может быть трансформирована практически любая эконометрическая модель в виде изолированного уравнения.
. Данная модель является базовой моделью эконометрики, потому что к такому виду может быть трансформирована практически любая эконометрическая модель в виде изолированного уравнения.
 , причём
, причём 
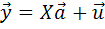 ). Вот компактная запись этой схемы
). Вот компактная запись этой схемы 
 - вектор известных значений эндогенной переменной yt модели;
- вектор известных значений эндогенной переменной yt модели; - вектор неизвестных значений случайных возмущений ut;
- вектор неизвестных значений случайных возмущений ut; - матрица известных значений предопределенной переменной wt модели, расширенная столбцом единиц; наконец,
- матрица известных значений предопределенной переменной wt модели, расширенная столбцом единиц; наконец, – вектор неизвестных коэффициентов уравнения модели.
– вектор неизвестных коэффициентов уравнения модели. . Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим:
. Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим: 
 значений эндогенной переменной yt, если:
значений эндогенной переменной yt, если:  .
. , где матрица коэффициентов, зависящих только от выборочных значений W предопределенной переменной wt
, где матрица коэффициентов, зависящих только от выборочных значений W предопределенной переменной wt



 .
. - вектор известных значений эндогенной переменной yt модели;
- вектор известных значений эндогенной переменной yt модели;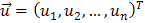 - вектор неизвестных значений случайных возмущений ut;
- вектор неизвестных значений случайных возмущений ut; - матрица известных значений предопределенной переменной x исходной модели, расширенная столбцом единиц (при наличии a0);
- матрица известных значений предопределенной переменной x исходной модели, расширенная столбцом единиц (при наличии a0); – вектор неизвестных коэффициентов уравнения модели.
– вектор неизвестных коэффициентов уравнения модели. . Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим:
. Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим: 
 значений эндогенной переменной yt, если:
значений эндогенной переменной yt, если:  .
.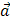 обозначим символом F.
обозначим символом F. , которая обладает одновременно двумя свойствами:
, которая обладает одновременно двумя свойствами: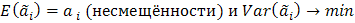 , i=0,1 (эффективности).
, i=0,1 (эффективности). .
. (k+1), где n>(k+1), обладает линейно-независимыми столбцами, а случайные возмущения удовлетворяют 4-м условиям:
(k+1), где n>(k+1), обладает линейно-независимыми столбцами, а случайные возмущения удовлетворяют 4-м условиям: (5)
(5) (6)
(6)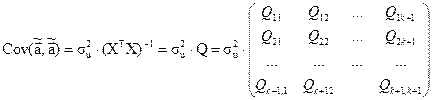 ; (7)
; (7) (8)
(8) в вектор наилучших оценок коэффициентов. Тогда наша задача построить
в вектор наилучших оценок коэффициентов. Тогда наша задача построить  , удовлетворяющим двум условиям оптимальности.
, удовлетворяющим двум условиям оптимальности. 

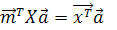
 . (12)
. (12) (из свойства Var(ax+by)=
(из свойства Var(ax+by)=  )
)

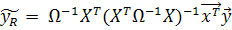 (13)
(13)
 .
.
 и
и  (теорема Фишера),
(теорема Фишера), , получим
, получим  (9)
(9) , тогда (9) превращается в (7)
, тогда (9) превращается в (7)
 . (1)
. (1)  (2)
(2) . (4)
. (4)
 как переменный, тогда вектор
как переменный, тогда вектор  оказывается функцией (аффинным преобразованием) вектора
оказывается функцией (аффинным преобразованием) вектора 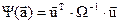 (5)
(5) .
.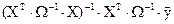 . Это обстоятельство и проясняет причину упомянутого выше названия данной процедуры – обобщённый метод наименьших квадратов.
. Это обстоятельство и проясняет причину упомянутого выше названия данной процедуры – обобщённый метод наименьших квадратов. =
=  , где
, где 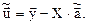 (9.37)
(9.37) , величина
, величина  имеет особенно простой вид:
имеет особенно простой вид: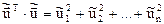 = ESS,
= ESS, .
.

 . Заметим, что при
. Заметим, что при  формула (*) превращается в выражение
формула (*) превращается в выражение 


