
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценивание параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков методом максимального правдоподобия (ммп).Содержание книги
Поиск на нашем сайте Задача: Пусть в схеме Гаусса-Маркова Решение: Будем предполагать, что объясняющие переменные в модели Для отыскания оценок параметров ММП составим функцию правдоподобия выборки
Ln L = -
Затем подставляем его во второе уравнение системы и после умножения этого уравнения на
33. Оценивание нелинейных по коэффициентам моделей множественной регрессии методом Гаусса-Ньютона (на примере модели динамического ряда с экспоненциальной функцией тренда).
Если нелинейная по коэффициентам функция регрессии операцией логарифмирования не трансформируется к линейной по коэффициентам, то возможен алгоритм линеаризации общей регрессионной модели, базирующийся на линеаризации ее гладкой (по предположению) функции регрессии в окрестности известных приближенных значений
Оценив модель, можем получить оценки коэффициентов исходной модели:
Каждая переменная
Рассмотрим модель динамического ряда с экспоненциальным трендом:
Стоит отметить, что функция регрессии является суммой нелинейной по коэффициентам функции тренда (показательной функции) и линейной по коэффициентам сезонной составляющей. Предстоит выполнить линеаризацию только показательной функции:
Шаг 1. Определяются приближенные значения Шаг 2. Используя обозначения:
Составим спецификацию линеаризованной регрессионной модели:
Далее необходимо оценить следующие параметры модели: Шаг 3. Составляем в рамках модели систему n уравнений наблюдений Шаг 4. При помощи функции ЛИНЕЙН оцениваем МНК эту модель Шаг 5. Используя правила, записываем МНК-оценку исходной модели В данном случае оценка 34. Спецификация и оценивание нелинейных по коэффициентам моделей множественной регрессии со специальными функциями регрессии (на примере производственной модели с функцией Кобба-Дугласа).
Данная модель именуется производственной функцией Кобба-Дугласа. В ней Y – уровень выпуска продукции за принятый отрезок времени; K и L – уровни соответственно основного капитала и живого труда, использованные в процессе выпуска величины Y. Видно, что функция не линейна по коэффициентам a=( Для того, чтобы прийти к уравнению, линейному по коэффициентам, используется операция логарифмирования: Ln Y = ln Функция LnY аргументов lnK и lnL линейна по коэффициентам y= Случайный остаток v имеет смысл включить в виде сомножителя, например:
Где v>-1, u=ln(1+v); После подобных преобразований, получили модель парной регрессии:
Пусть случайный остаток u удовлетворяет всем предпосылкам теоремы Гаусса-Маркова. Пусть по обучающей выборке
Прошедшая проверку адекватности. Для расчета прогноза 1. Найдем
2. Рассчитаем прогноз и стандартную ошибку величины
Представим оцененную исходную спецификацию:
Где коэффициенты вычислены по формулам
Все этапы по порядку: Шаг 1. В процессе спецификации эконометрических моделей с нелинейными по коэффициентам стандартными функциями регрессии случайные остатки следует включать в поведенческие уравнения в виде соответствующих сомножителей. Затем поведенческое уравнение операцией логарифмирования трансформируется в модель линейной регрессии. Шаг 2. Построив трансформированную линейную модель, следует обратным преобразованием (потенцированием) получить оценку исходной нелинейной модели. Шаг 3. Прогноз эндогенной переменной исходной нелинейной модели можно строить либо при помощи прогноза ее логарифма, полученного по оценке трансформированной линейной модели, либо же по оценке исходной модели. Ш а г 4. Стандартная ошибка прогноза рассчитывается по формуле S 35. Оптимальное точечное прогнозирование значений эндогенной переменной по линейной модели (случай гомоскедастичного и неавтокоррелированного случайного остатка) на примере модели Оукена. Рассмотрим модель Оукена: где
Обозначим,
При наличии информации об объекте-оригинале (выборки), наилучший точечный прогноз вычисляется по правилу: Стандартная ошибка прогноза: В случае модели Оукена Т.о. точность прогноза падает по мере удаления значения
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 вектор случайных остатков с числовыми характеристиками
вектор случайных остатков с числовыми характеристиками  ,
,  , имеет нормальный закон распределения. Требуется оценить параметры
, имеет нормальный закон распределения. Требуется оценить параметры  и
и  модели методом максимального правдоподобия.
модели методом максимального правдоподобия.
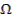 полагаем известной. Из
полагаем известной. Из  следует, что вектор
следует, что вектор  тоже обладает нормальным законом распределения
тоже обладает нормальным законом распределения 
 (
( и
и  .
.
 (
(
 . Найдем его производные по аргументам и приравняем их к нулю:
. Найдем его производные по аргументам и приравняем их к нулю: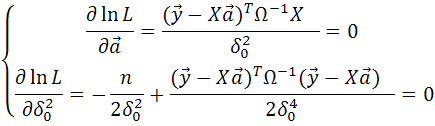
 ) находим
) находим  :
:
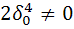 находим
находим  =
=  , где
, где  . Полученные величины образуют решение системы и являются искомыми ММП-оценками параметров.(эффективной и ассимптотически несмещенной)
. Полученные величины образуют решение системы и являются искомыми ММП-оценками параметров.(эффективной и ассимптотически несмещенной)
 =(
=( ) коэффициентов
) коэффициентов  :
: , где
, где  =
= 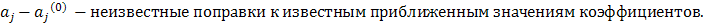 Принимая обозначения
Принимая обозначения  ,
,  получим регрессионную модель с однородной линейной функцией регрессии
получим регрессионную модель с однородной линейной функцией регрессии
 =
=  +
+  , S
, S 
 линеаризованной модели является функцией объясняющих переменных
линеаризованной модели является функцией объясняющих переменных  исходной модели, от приближенных коэффициентов
исходной модели, от приближенных коэффициентов  функция
функция 

 коэффициентов показательной функции. Далее эти величины будут интерпретироваться как константы.
коэффициентов показательной функции. Далее эти величины будут интерпретироваться как константы.





 будет иметь смысл ожидаемого темпа прироста уровней эндогенной переменной за каждый квартал после устранения сезонной составляющей. По полученной модели может проведена проверка на адекватность модели.
будет иметь смысл ожидаемого темпа прироста уровней эндогенной переменной за каждый квартал после устранения сезонной составляющей. По полученной модели может проведена проверка на адекватность модели.
 ,
, 
 lnK + (1-
lnK + (1-  ,
,  . В силу функциональной зависимости
. В силу функциональной зависимости 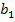 и
и  уравнение можно еще упростить:
уравнение можно еще упростить: +
+  , где y=ln Y – ln L=ln(
, где y=ln Y – ln L=ln(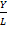 ); x=ln K – ln L= ln(
); x=ln K – ln L= ln( )
)
 .
.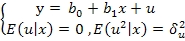
 получена МНК-оценка преобразованной модели:
получена МНК-оценка преобразованной модели:
 по соответствующим значениям
по соответствующим значениям  выполним:
выполним: = ln(
= ln(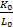 ) и вычислим оптимальный прогноз величины
) и вычислим оптимальный прогноз величины  = ln (
= ln ( :
:
 :
: =
=  exp(
exp( S
S  =
= 
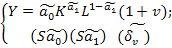
 ,
,  ,
, 
 =
=  .
.
 - темп прироста ВВП,
- темп прироста ВВП,  - изменение уровня безработицы,
- изменение уровня безработицы,  - случайный остаток. Пусть модель оценена МНК по выборке
- случайный остаток. Пусть модель оценена МНК по выборке  . Т.о. имеем,
. Т.о. имеем,
 значение экзогенной переменной, при котором необходимо вычислить прогноз ВВП.
значение экзогенной переменной, при котором необходимо вычислить прогноз ВВП.  - прогноз,
- прогноз,  - наблюденное в реальности значение ВВП.
- наблюденное в реальности значение ВВП.


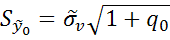 , где
, где  ,
, 




