
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблема, симптомы мультиколлинеарности. Методика отбора регрессоров в линейной модели в ситуации мультиколлинеарности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). Включение в модель мультиколлинеарных факторов нежелательно по следующим причинам: · затрудняется интерпретация параметров множественной регрессии; · параметры линейной регрессии теряют экономический смысл; · оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений, что делает модель непригодной для анализа и прогнозирования Симптомы: а) резкое изменение значений оценок модели при незначительной вариации состава обучающей выборки; б) наличие в оцененной модели небольших по модулю значений в) большое значение коэф-та детерминации между каждой объясняющей пер-ой линейной модели и ее остальными объясняющими пер-ми. Поэтому, если в модели возникла ситуация мултиколлинеарности, то из состава объясняющих пер-х модели следует вывести дублирующие друг друга пер-е. Решению проблемы устранения мультиколлинеарности факторов может помочь и переход к уравнениям приведенной формы. С этой целью в уравнение регрессии производится подстановка рассматриваемого фактора через выражение его из другого уравнения. Метод главных компонент применяется для исключения или уменьшения мультиколлинеарности объясняющих переменных регрессии. Основная идея заключается в сокращении числа объясняющих переменных до наиболее существенно влияющих факторов. Это достигается путем линейного преобразования всех объясняющих переменных xi (i=0,..,n) в новые переменные, так называемые главные компоненты. При этом требуется, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех объясняющих переменных xi (i=0,..,n). Второй компоненте — максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается и т. д.
57. Эконометрические модели в виде систем линейных одновременных уравнений (СЛОУ): примеры и проблема идентификации (на примере модели спроса-предложения блага). Системы одновременных уравнений. Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых, кроме объясняющих переменных, может включать в себя объясняемые переменные из других уравнений системы. Системы одновременных уравнений могут быть использованы для моделей национальной экономики. Ярким примером системы одновременных уравнений служит модель спроса и предложения. Пусть QtD – спрос на товар в момент времени t, QtS -предложение товара в момент времени t, Рt – цена на товар в момент времени t, Yt - доход в момент t. Составим систему уравнений "спрос - предложение": QtS = α1 + α2 Рt +a3 Рt-1 + ξt (предложение), QtD = β1 + β2 Рt + β3 Yt + ut (спрос), QtS =QtD (равновесие). Цена товара, Рt и спрос на товар Qt = QtD = QtS определяются из уравнений модели, то есть являются эндогенными переменными Объясняющими переменными в данной модели являются доход Yt и значение цены товара в предыдущий момент времени Рt-1. Проблема идентификации для эконометрических моделей в виде системы одновременных уравнений. При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификации – это единственность соответствия между приведенной и структурной формами модели. Проблема идентификации существует только для системы одновременных уравнений. Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметром структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Пример:
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Пример
Модель содержит восемь структурных коэффициентов, что соответствует выражению n • (n— 1 + т).Структурная модель полном виде, содержащая п эндогенных и т предопределенных переменных в каждом уравнении системы, всегда неидентифицируема.
58. Эконометрические модели в виде систем линейных одновременных уравнений (СЛОУ): примеры и проблема оценивания параметров структурной формы (на примере макромодели Кейнса). Отдельные регрессионные уравнения системы в качестве предопределённых переменных могут включать как объясняющие переменные, та и объясняемые переменные из других уравнений. Такие системы называются системами одновременных уравнений. Две проблемы: проблема идентифицируемости, проблема оценивания параметров уравнений. Рассмотрим вторую проблему. Существо этой проблемы рассмотрим на примере модели Кейнса. Данная модель имеет вид:
Запишем приведенную форму этой модели:
Рассматривая эти уравнения, мы констатируем, что Y является линейной функцией случайного остатка U. Поэтому значение Y коррелирует со значением случайного остатка( 59. Необходимое условие идентифицируемости поведенческого уравнения модели СЛОУ (правило порядка). Сверхидентифицируемость параметров поведенческого уравнения. Линейная модель одновременных уравнений (ЛМОУ).
В компактной записи модели квадратная м-ца А=(аij) состоит из коэф-тов при эндог пер-х и предполагается невырожденной. i-е поведенческое ур-е модели может быть разрешено относительно пер-й Теорема. Пусть в ситуации (1.2) i-е поведенческое ур-е модели (1.1) идентифицируемо. Тогда справедливо неравенство К-Ki>Gi-1 (17.29) где Кi, — количество предопределенных переменных модели, входящих в г-с уравнение; Gi — количество эндогенных переменных модели, входящих в i-е уравнение модели. Рассматривая неравенство (17.29), можем сказать, что если i-c поведенческое уравнение модели (1.1) идентифицируемо, то количество К – Кi, предопределенных переменных, не входящих в данное уравнение, по крайней мере на единицу больше количества G, эндогенных переменных, входящих в это уравнение. Замечание. Подчеркнем, что справедливость неравенства (17.29) является необходимым условием ндешифицируемостн i-io уравнения. Это значит, что когда неравенство (17.29) несправедливо, га i-e уравнение заведомо неидентифицируемо. Однако при выполнении неравенства (17.29) еще нельзя сделать выводи об идентифицируемости данного уравнения. Так, условие (17.29), именуемое правилам порядка, позволяет выявлять неидентифицируемыс уравнения модели (17.22), но не дает возможности отмечать ее идентифицируемые уравнения. Такую возможность доставляет критерий (необходимое и достаточное условие), рассмотренный ниже. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. Пример:
Структурная модель всегда представляет собой систему сон местных уравнений, каждое из которых необходимо проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Для того чтобы уравнение было идентифицируемо, нужно, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного. Правило ранга. Чтобы сформулировать критерий идентифицируемости i-ro уравнения (1.1), потребуется понятие ограничений на его коэффициенты. Определение 17.1. Ограничениями на коэффициенты i-ro уравнения модели (1.1) называется система из однородных линейных алгебраических уравнений
которым априорно удовлетворяет вектор коэффициентов i-го уравнения модели (1.1). Итак, полагаем, что для i-го поведенческого уравнения модели (1.1) построена матрица Ri ограничений (17.30), состоящая из Li строк и G + К столбцов. Подчеркнем, что Li < G + К. Добавим, что Li — количество переменных модели (1.1), не входящих в i-e уравнение. Обозначим символом
расширенную матрицу ЛМОУ. Матрица (17.36) содержит G строк и G+ К столбцов. Элементами i-й строчки матрицы (17.36) являются компоненты вектора (17.31). Все готово для формулировки критерия идентифицируемости поведенческих уравнений модели (1.1) из линейных одновременных линейных уравнений. Теорема 17.2. В ситуации (1.1) i-е уравнение модели (1.1) из линейных одновременных уравнений идентифицируемо тогда и только тогда, когда справедливо равенство rk( где rk( Доказательство этого важного для эконометрики утверждения, именуемого правилам ранга, предлагается получить в процессе
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 при достаточно высоком значении коэф-та детерминации;
при достаточно высоком значении коэф-та детерминации;



 ). Следовательно, в рамках модели Кейнса оказывается нарушенной последняя предпосылка теоремы ГМЭ. Можно показать, что нарушение этой предпосылки порождает несостоятельность оценок параметров
). Следовательно, в рамках модели Кейнса оказывается нарушенной последняя предпосылка теоремы ГМЭ. Можно показать, что нарушение этой предпосылки порождает несостоятельность оценок параметров 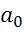 ,
,  , ни МНК, ни ВМНК, ни ОМНК.
, ни МНК, ни ВМНК, ни ОМНК.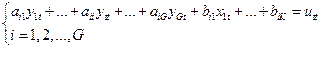
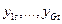 - эндогенные, G – их количество
- эндогенные, G – их количество - предопределенные, К – кол-во
- предопределенные, К – кол-во , при этом справедливо рав-во:
, при этом справедливо рав-во:  =1. Оно именуется условием нормализации.
=1. Оно именуется условием нормализации.
 (17.30)
(17.30) (17.31)
(17.31) = (А|В) (17.36)
= (А|В) (17.36) ) = G-l, (17.37)
) = G-l, (17.37)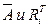 .
.


