Устойчивость линейных дискретных систем

Исследование дискретных с-м начинается с оценки их работоспособности, т.е. устойчивости. В классе линейных систем задача решается так же, как и в теории линейных непрерывных САУ, но с учетом особенностей, связанных с квантованием сигналов. Устойчивость для дискретных с-м опр. по поведению переходной составляющей y_n(t) общего решения однородного диф. ур-ния исследуемой с-мы. Общее решение представляет собой сумму: y(iT_n)=y_в(iT_n)+y_n(iT_n), где y_в(iT_n) вынужденная составляющая процесса, зависящая от внешнего воздействия, а y_n(iT_n)=ⁿΣ_k=1 A_k zⁱ_k переходн. составляющая, т.е. сумма экспоненциальных дискретных ф-ций. zⁱ_k = e_k^piTn. z_k - корни характеристического ур-ния замкнутой системы.

Дискретная с-ма называется устойчивой, если с течением времени y_n(iT_n) стремится к нулю. Примеры на рис., где а и б монотонные, в и г - колебательные процессы устойчивых и неустойчивых сис-м. При i → ∞ y_n(iT_n) будет равна нулю, если все корни z_k характеристического ур-ния D*(z) = 0 по модулю будут меньше единицы: |z_k| < 1. Устойчивые (а и в) и неустойч. (б и г) процессы в дискрет. с-мах.

Таким образом, необходимое и достаточное условие устойчивости линейных дискретных с-м: замкнутая система будет устойчивой, если корни характеристического уравнения D*(z) = 0 находятся внутри круга единичного радиуса. Если речь идет об устойчивости разомкнутой системы, то оценивается расположение корней уравнения Q*(z) = 0 и применяются сформулированные выше условия.

 

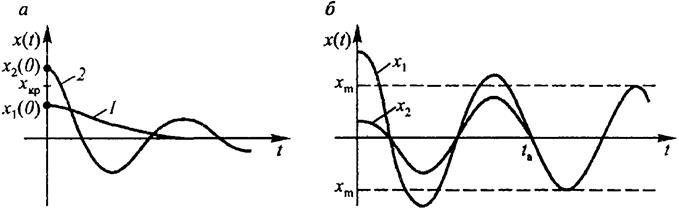
Свойства нелинейных систем

САУ явл. нелинейной, если хотя бы один ее конструктивный элемент описывается нелинейн. ур-м. Если переменные y(t), x(t) и их производные входят в диф.ур. в виде произведений, частных или степеней, то ур-ние явл. нелинейным. Практически все реальные САУ содержат 1 или несколько нелинейных эл-в (нелинейностей).

Различают два вида нелинейных элементов, существенно нелинейные и несущественно нелинейные. Нелинейность считается несущественной, если ее замена линейным эл-м не изменяет принципиальных особенностей с-мы и процессы в с-ме не отличаются от процессов в реальной системе. В противном случае - существенная. САУ с существенными нелинейностями имеет особенности, кот. не присущи линейным с-м. Главная особенность в том, что они не подчиняются принципу наложения, а характер и показатели переходного процесса зависят от величины внешнего воздействия или начального отклонения.

Например, при малом начальном отклонении x1(0), меньшем некот. критического значения х_кр, переходный процесс может быть апериодическим (а - линия 1), а при большом начальном отклонении х2(0) > хкр - колебательным (а - линия 2).

Другой важной особенностью явл. зависимость условий устойчивости от величины внешнего воздействия: САУ, устойчивая при одних значениях начального отклонения, оказывается неустойчивой при других его значениях. На рис. б показаны переходные процессы х1 и х2, один из кот. вызван большим начальным отклонением и сходится к устойчивому колебательному процессу, а второй, вызванный малым начальным отклонением, расходится и тоже стремится к колебательному процессу.

При анализе нелинейн. С-м обычно решают следующие задачи: 1) отыскание возможных состояний равновесия с-мы и оценка их устойчивости; 2) определение возможности сущ-ния автоколебаний и оценка их устойчивости; 3) выявление соотношений между параметрами с-мы, при кот. возникают автоколебания; 4) опр. параметров автоколебаний и их связи с параметрами с-мы.

Типовые виды нелинейности

Можно выделить 3 группы нелинейных звеньев: Нелинейные звенья с однозначными хар-ми (статич. нелинейности). Однозначная хар-ка звена свидетельствует о том, что кроме наличия чувствительности к значению входной координаты, звено нечувствительно ни к направлению движения входн. координаты ни к её производным. Модели таких звеньев можно составить без применения блоков с эффектом памяти (интеграторов, регистров задержки). Спец. моделирующие программы имеют в своих библиотеках готовые блоки с однозначными нелинейностями. Звенья: "Зона нечувствительности", "Ограничение", "Реле двухпозиционное без гистерезиса", "Реле трехпозиционное без гистерезиса", "АЦП без гистерезиса"

Нелинейные звенья с многозначн. хар-ми (динамич. нелинейности). Многозначная характеристика звена свидетельствует о том, что звено чувствительно либо к направлению её движения, либо к значению её производных. Модели таких звеньев невозможно составить без применения блоков с эффектом памяти (интеграторов, регистров задержки, звеньев чистого запаздывания). Программы могут иметь соответств. составные модели - нелинейн. звенья с многозначными характ-ми. Звенья: "Реле двухпозиционное с положительным или с отрицательным гистерезисом", "Реле трехпозиционное с положительным или с отрицательным гистерезисом", "Люфт","Упор", "Сухое трение", "Магнитный гистерезис"

Особые нелинейные элементы (не поддаются классификации). К группе особых нелинейных звеньев относят те, чьи свойства уникальны и не поддаются классификации. Некоторым особым нелинейным звеньям свойственен атрибут функциональной завершенности. Др. особые звенья, например, "множительное" или "ψ-ячейка" часто входят, как составные части, в блок-схемы более сложных звеньев с неоднозначными характеристиками. Звено множительное. Звено с параболической четной характеристикой. Звено с параболической нечетной характеристикой. Звено "ψ-ячейка".