Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система «Станок-процесс резания» как объект управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система «Станок-процесс резания» как объект управления Станок вместе с процессом рез. можно отнести к сложным ОУ с наличием входных и выходных переменных. Сложность ОУ проявляется в значит. числе параметров, определяющих течение процесса резания, в большом числе внутренних связей между пар-ми, в частности, в таком их взаимном влиянии, при кот. изменение одного параметра вызывает нелинейное изменение др. Отмеченная сложность усиливается возникновением обратных связей между пар-ми, изменяющими ход процесса резания. Рассмотрим станок с ЧПУ совместно с процессом обр-ки на нем с учетом того, что он явл., и замкнутой с-мой взаимодействия упругой с-мы с раб. процессами, но и звеном направленного действия в с-ме автоматич. управления механич. обр-кой. После считывания управляющая программа подвергается в с-ме ЧПУ обратному процессу декодирования, т. е. систему управления отличает дискретный хар-р задания и прохождения сигналов. Координатами вектора управляемой величины явл. показатели результатов процесса механической обр-ки: точность размера детали, т.е. разность между фактически полученными и заданными размерами; параметры шерох-ти обработанных пов-тей; производительность обр-ки Q, характ-мая кол-вом Ме, снятого в процессе обр-ки в ед. времени; экономичность обр-ки Е, хар-мая затратами на снятие припуска. Отклонения разм-в деталей при обр-ке на станках происходят из-за погрешностей, обусловленных несовершенством механич. части станка, инстр-та и раб. мех-мов, а также из-за погрешностей, связанных с с-мой управления. Погрешности: воспроизведения (статич. и динамич. ошибки приводов подач), программы (ошибки аппрокс.), вносимые шумами каналов связи. Основной частью ОУ явл. процесс резания, представляющий собой сложн. физ. процесс, при кот. возникают упругие и пластические деформации, сопровожд. трением, тепловыделением, наростообразованием, усадкой стружки, упрочнением, изнашиванием реж. инстр-та и др. Производительность обр-ки зависит от парам-ров резания, кот. опр. технолог и закладывает в программу. В процессе обр-ки возмущающие воздействия приводят к отклонениям парам-в технол. процесса. Классификация систем автоматического управления Теория АУ, изуч. процессы автоматич. управления объектами физической природы, и при помощи математич. средств выявляются свойства систем автоматич. управления и разрабатываются рекомендации по их проектированию. Сущ. Большое разнообразие СУ. А также несколько признаков классификации. По назнач., т.е. хар-ру изменения задающ. воздействия, различают: с-мы автоматич. стабилизации (алгоритм функ-ния кот. содержит предписание поддерживать значение управляемой величины постоянным, x=const); с-мы программного управления (алгоритм функц-ния кот. содержит предписание изменять управляемую величину в соответствии с заранее заданной функцией времени); следящие системы (алгоритм функ-ния кот. содержит предписание изменять управляемую величину в соответствии с заранее неизвестной ф-цией времени). В стабилизирующих, программных и следящих АСУ цель управления заключается в обеспечении равенства или близости управляемой величины x(t) к ее заданному значению. По принципу управления: С-мы с управлением по разомкнутому циклу (не осущ. контроль управляемой величины, т.е. входными воздействиями явл. только внешние воздействия.); с управлением по замкнутому циклу (входными воздействиями явл. внутреннее воздействия); комбинированного управления (в кот. входными воздействиями явл. как внешн., так и внутр. воздействия.). По хар-ру использ-х для управления сигналов: непрерывные или аналоговые САУ (в кот. действуют непрерывные (аналоговые), определенные в каждый момент времени сигналы); дискретные САУ (действует хотя бы один дискретный, определенный только в некоторые моменты времени сигнал), из кот. выделяют: импульсные; релейные; цифровые САУ. По хар-ру математических соотношений: линейные САУ, для которых справедлив принцип суперпозиции (все элементы кот. описываются линейными диф.ур-ми); нелинейные (хотя бы один элемент кот. описывается нелинейными диф. или алгебраич. ур-ми). По количеству выходных координат объекта управления: одномерные; многомерные. По степени зависимости управляемой величины в установившемся режиме от величины возмущающего воздействия: статические (имеется зависимость управляемой величины в установившемся режиме от величины возмущ. воздействия); астатические (отсутствует). В зависимости от принадлежности источника энергии, при помощи кот. создается управляющ. воздействие, различ. АСУ: прямого действия (управл. воздействие создается при помощи энергии объекта управления); непрямого действия (управляющее воздействие создается за счет энергии доп. источника). Позиционные звенья Типовыми динамич. звеньями наз. звенья, описываемые ДифУр не выше 2-го порядка. Такие звенья классифиц-ся в зависимости от вида левой и правой частей ур-ния. Все типовые звенья можно разделить на 3 группы: Позиционные, Интегрирующие и Дифференцирующ. звенья. Позиционные звенья - звенья, в кот. выходн. и входн. величины в установившемся режиме связаны линейн. зависимостью y(t)=kg(t). А переходная ф-ция будет иметь вид W(s)=k 1. Идеальн. усилительн. (безынерционное) звено, ур-ние в стандартной форме: y(t)=kg(t), где k=
Интегрирующие звенья Типовыми динамич. звеньями наз. звенья, описываемые ДифУр не выше 2-го порядка. Такие звенья классифиц-ся в зависимости от вида левой и правой частей ур-ния. Все типовые звенья можно разделить на 3 группы: Позиционные, Интегрирующие и Дифференцирующ. звенья. Интегрирующие звенья: C(p)y=k*x/p, C(p)p=0=1. 1. Идеальное интегрирующ. звено. Если постоянная времени звена значительно меньше последующего за ним. y=k*x/p; dy/dt=kx; Wp = k/p.
2. Изодромное звено - W (p) = k1 /p+k2, где k1 и k2 - передаточн. коэф. PY = (k1 + k2 p)x. W(p)=k(Tp+1)/p, T = k1/k2. Изодромное звено представляет собой дифференцирующ. звено с замлением и интегрирующ., вкл. последовательно. Его можно представить в виде совокупности двух звеньев соединеннных параллельно: идеального интегрирующего с k1 и параллельно включенного безинерционного с k2. Примером интегрирующ. звена может служить гидравлич. исполнительный мех-м кот. находит широкое прим. в современных сис-х регулир-ния.
Входной величиной для него является перепад давлений ∆Рвх, а выходной - перемещение ∆Sвых поршня. Сила давления на поршень равна fn=(P01-P02)F, где F – эффективн. площадь поршня. Если пренебречь трением и инерцией поршня и связанных с ним масс, то можно считать, что это усиление целиком расходуется на преодоление внешней нагрузки, приложенной к поршню (сопротивление перемещению регулирующего органа, заслонки и т. п.). Дифференцирующее звено Типовыми динамич. звеньями наз. звенья, описываемые ДифУр не выше 2-го порядка. Такие звенья классифиц-ся в зависимости от вида левой и правой частей ур-ния. Все типовые звенья можно разделить на 3 группы: Позиционные, Интегрирующие и Дифференцирующ. звенья. Дифференцирующее звено. Выходн. величина дифференц-го звена пропорциональна производной по времени от входн. величины: xвых=k(dxвх/dt). W(p)=kp. Если входн. и выходн. величины имеют одинаковую размерность, то коэф. k изм-ся в сек. В этом случае его принято обозначать через Т и наз. постоянной времени диф-го звена. 1. Идеальное диф-щее звено. Уравнение:
Переходн. ф-ция звена при х 1 = 1(t); A (t) = k 1 ’ (t) = k w(t) представляет собой импульсную функцию, площадь которой равна k. 2. Реальное диф-щее звено. Уравнение:
Усилители Усилители предназначены для ув. мощности сигнала на выходе измерительной части САУ, т.к. часто она недостаточна для приведения в действие исполнительных устройств. Главным параметром явл. стабильность хар-ки, большой частотный диапазон и отсутствие искажения сигнала, а также КПД и выходн. мощность. В САУ испол. обычные усил., усилители-преобразователи, операционные усилители, осущ. моделирование различн. математич. операций (суммир., диф., интегр.и т. д.). В электрических с-мах исп. электронные, электромагнитн. и при больших мощностях электромашинные, а в неэлектрических – механич., пневматич. и гидравл. усилители. Электронные усилители делят на ламповые и полупроводниковые (экономич-ть, мгновен. готовность к работе, высок. коэф. усиления и большой диапазон усиливаемых частот, а также вибро- и ударостойкость). По виду усиливаемого сигнала усилители делятся на усилители тока (перемен. и постоян.). По принципу действия их классифицируют на усилители дискретного (релейного) и аналогового действия.
В общем случае полупроводниковый усилитель состоит из входного устройства ВУ, многокаскадного усилителя напряжения УН, усилителя мощности УМ, источника питания ИП и цепи обратной связи ОС. При этом усилители переменного тока содержат только входной трансформатор Т, а постоянного тока - еще и вибропреобразователь ВП. В процессе работы усилителя входной сигнал напряжения постоянного тока преобразуется с помощью ВП в пульсирующее напряжение и через трансформатор Т подается в пятикаскадный усилитель напряжения переменного тока УН. Затем усиленные сигналы поступают в усилитель мощности УМ, а из него Uвых направляется в цепь исполнительного органа. Через цепь обратной связи ОС выходной сигнал возвращается на вход 3-го каскада усилителя напряжения. Источник питания ИП состоит из силового трансформатора и двух выпрямителей, один из кот. питает усилитель напряжения, а другой - мощности. Дискретное управление В зависимости от способа формирования управляющих воздействий САУ разделяются на системы непрерывного и дискретного управления. В непрерывном управлении любая информация для управления в любой момент времени, а также управляющие воздействия непрерывны во времени и по величине. Связи между элементами сохраняются всегда (б). Дискретное управление хар-ся наличием хотя бы одного звена при прерывистом изменении управляющих воздействий (в-е).Способы управления в САУ: а и б непрерывное; в амплитудно-импульсное; г широтно-импульсное. д частотноимпульсное; е - релейное
Дискретное управление различается на импульсное и релейное. Импульсное управление классиф-ся: амплитудно-импульсное; широтно-импульсное; частотно-импульсное и др. В амплитудно-импульсном управлении алгоритм управления обеспечивается измен-м амплитуды импульсов при неизменных остальных параметрах импульсной последовательности. В широтно-импульсном управлении алгоритм управления обеспечивается изменением длительности импульсов при неизменных остальных параметрах импульсной последовательности. В частотно-импульсном управлении алгоритм управления обеспечивается изменением частоты (периода) следования импульсов при неизменных остальных параметрах импульсной последовательности. В сложных с-мах управления используется помехозащищенный метод управления с помощью кодо-фазо-манипуляции. Дискретное управление широко применяется в цифровых управляющих машинах. Запасы устойчивости При оценке устойчивости САУ одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т.е. степени удаленности с-мы от границы устойчивости. Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины - запас устойчивости по фазе ∆φ и запас устойчивости по амплитуде ∆G (рис 1).
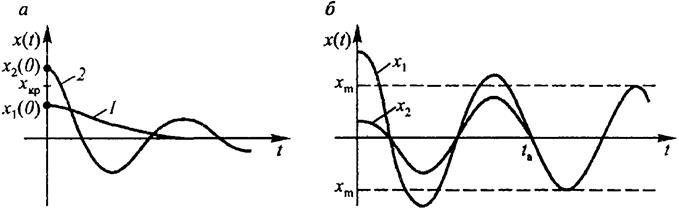
Запас устойчивости по фазе определяется величиной ∆φ, на кот. должно возрасти запаздывание по фазе в с-ме с частотой среза, чтобы с-ма оказалась на границе устойчивости. Запас устойчивости по амплитуде опр. величиной ∆G допустимого подъема ЛАЧХ, при кот. с-ма окажется на границе устойчивости. Т.е., запас по амплитуде представляет собой запас по коэф. передачи разомкнутой цепи по отношению к его граничному по устойчивости значению: Свойства нелинейных систем САУ явл. нелинейной, если хотя бы один ее конструктивный элемент описывается нелинейн. ур-м. Если переменные y(t), x(t) и их производные входят в диф.ур. в виде произведений, частных или степеней, то ур-ние явл. нелинейным. Практически все реальные САУ содержат 1 или несколько нелинейных эл-в (нелинейностей). Различают два вида нелинейных элементов, существенно нелинейные и несущественно нелинейные. Нелинейность считается несущественной, если ее замена линейным эл-м не изменяет принципиальных особенностей с-мы и процессы в с-ме не отличаются от процессов в реальной системе. В противном случае - существенная. САУ с существенными нелинейностями имеет особенности, кот. не присущи линейным с-м. Главная особенность в том, что они не подчиняются принципу наложения, а характер и показатели переходного процесса зависят от величины внешнего воздействия или начального отклонения. Например, при малом начальном отклонении x1(0), меньшем некот. критического значения хкр, переходный процесс может быть апериодическим (а - линия 1), а при большом начальном отклонении х2(0) > хкр - колебательным (а - линия 2). Другой важной особенностью явл. зависимость условий устойчивости от величины внешнего воздействия: САУ, устойчивая при одних значениях начального отклонения, оказывается неустойчивой при других его значениях. На рис. б показаны переходные процессы х1 и х2, один из кот. вызван большим начальным отклонением и сходится к устойчивому колебательному процессу, а второй, вызванный малым начальным отклонением, расходится и тоже стремится к колебательному процессу.
При анализе нелинейн. С-м обычно решают следующие задачи: 1) отыскание возможных состояний равновесия с-мы и оценка их устойчивости; 2) определение возможности сущ-ния автоколебаний и оценка их устойчивости; 3) выявление соотношений между параметрами с-мы, при кот. возникают автоколебания; 4) опр. параметров автоколебаний и их связи с параметрами с-мы. Типовые виды нелинейности Можно выделить 3 группы нелинейных звеньев: Нелинейные звенья с однозначными хар-ми (статич. нелинейности). Однозначная хар-ка звена свидетельствует о том, что кроме наличия чувствительности к значению входной координаты, звено нечувствительно ни к направлению движения входн. координаты ни к её производным. Модели таких звеньев можно составить без применения блоков с эффектом памяти (интеграторов, регистров задержки). Спец. моделирующие программы имеют в своих библиотеках готовые блоки с однозначными нелинейностями. Звенья: "Зона нечувствительности", "Ограничение", "Реле двухпозиционное без гистерезиса", "Реле трехпозиционное без гистерезиса", "АЦП без гистерезиса" Нелинейные звенья с многозначн. хар-ми (динамич. нелинейности). Многозначная характеристика звена свидетельствует о том, что звено чувствительно либо к направлению её движения, либо к значению её производных. Модели таких звеньев невозможно составить без применения блоков с эффектом памяти (интеграторов, регистров задержки, звеньев чистого запаздывания). Программы могут иметь соответств. составные модели - нелинейн. звенья с многозначными характ-ми. Звенья: "Реле двухпозиционное с положительным или с отрицательным гистерезисом", "Реле трехпозиционное с положительным или с отрицательным гистерезисом", "Люфт","Упор", "Сухое трение", "Магнитный гистерезис" Особые нелинейные элементы (не поддаются классификации). К группе особых нелинейных звеньев относят те, чьи свойства уникальны и не поддаются классификации. Некоторым особым нелинейным звеньям свойственен атрибут функциональной завершенности. Др. особые звенья, например, "множительное" или "ψ-ячейка" часто входят, как составные части, в блок-схемы более сложных звеньев с неоднозначными характеристиками. Звено множительное. Звено с параболической четной характеристикой. Звено с параболической нечетной характеристикой. Звено "ψ-ячейка". Правило прим. критерия Попова: На комплексной плоскости строим модиф. годограф. Отмечаем т. -1/к, опр. сектором нелинейности. Пытаемся провести через т. какую-нидь прямую с наклоном q, чтобы годограф был правее. С-ма абсолютно устойчивой, если это возможно. Система «Станок-процесс резания» как объект управления Станок вместе с процессом рез. можно отнести к сложным ОУ с наличием входных и выходных переменных. Сложность ОУ проявляется в значит. числе параметров, определяющих течение процесса резания, в большом числе внутренних связей между пар-ми, в частности, в таком их взаимном влиянии, при кот. изменение одного параметра вызывает нелинейное изменение др. Отмеченная сложность усиливается возникновением обратных связей между пар-ми, изменяющими ход процесса резания. Рассмотрим станок с ЧПУ совместно с процессом обр-ки на нем с учетом того, что он явл., и замкнутой с-мой взаимодействия упругой с-мы с раб. процессами, но и звеном направленного действия в с-ме автоматич. управления механич. обр-кой. После считывания управляющая программа подвергается в с-ме ЧПУ обратному процессу декодирования, т. е. систему управления отличает дискретный хар-р задания и прохождения сигналов. Координатами вектора управляемой величины явл. показатели результатов процесса механической обр-ки: точность размера детали, т.е. разность между фактически полученными и заданными размерами; параметры шерох-ти обработанных пов-тей; производительность обр-ки Q, характ-мая кол-вом Ме, снятого в процессе обр-ки в ед. времени; экономичность обр-ки Е, хар-мая затратами на снятие припуска. Отклонения разм-в деталей при обр-ке на станках происходят из-за погрешностей, обусловленных несовершенством механич. части станка, инстр-та и раб. мех-мов, а также из-за погрешностей, связанных с с-мой управления. Погрешности: воспроизведения (статич. и динамич. ошибки приводов подач), программы (ошибки аппрокс.), вносимые шумами каналов связи. Основной частью ОУ явл. процесс резания, представляющий собой сложн. физ. процесс, при кот. возникают упругие и пластические деформации, сопровожд. трением, тепловыделением, наростообразованием, усадкой стружки, упрочнением, изнашиванием реж. инстр-та и др. Производительность обр-ки зависит от парам-ров резания, кот. опр. технолог и закладывает в программу. В процессе обр-ки возмущающие воздействия приводят к отклонениям парам-в технол. процесса.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.122 (0.01 с.) |

 , где N(s), L(s) - многочлены. Примеры реализации звена: механич. передачи (рычаги, редукторы) при их тщательном изготовлении, электр. усилители, делитель напряжений.
, где N(s), L(s) - многочлены. Примеры реализации звена: механич. передачи (рычаги, редукторы) при их тщательном изготовлении, электр. усилители, делитель напряжений. -коэф. передачи. Передат. ф-ция для идеальн. звена: W(s)=k. 2. Усилительн. звено с запаздыванием: y(t)=kg(t-t), где k=
-коэф. передачи. Передат. ф-ция для идеальн. звена: W(s)=k. 2. Усилительн. звено с запаздыванием: y(t)=kg(t-t), где k=  +y(t)=kg(t), где k=
+y(t)=kg(t), где k=  -постоян. времени. В операторной форме: (T1 p+1)y(t)=kg(t). Передаточ. ф-ция для апериодического звена: W(s)=
-постоян. времени. В операторной форме: (T1 p+1)y(t)=kg(t). Передаточ. ф-ция для апериодического звена: W(s)=  . 4. Неустойчивое апериодическое звено 1-го порядка: T
. 4. Неустойчивое апериодическое звено 1-го порядка: T  . 5. Апериодич. звено 2-го порядка:
. 5. Апериодич. звено 2-го порядка: 
 +T1
+T1 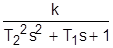 . 6. Колебательн. (устойчивое) звено:
. 6. Колебательн. (устойчивое) звено: 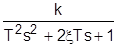 .
.
 Рис – передаточн. ф-ция и переходный процесс интегрирующего звена. На практике сущ. интегрирующие звенья с замедлением. (Tp+1)y=kx/p, где (Tp+1) - замедление W (p)=к/(Tp+1). Пример - электродвигатель постоянного тока, у кот. в качестве выходной величины рассмат-ся угол поворота.
Рис – передаточн. ф-ция и переходный процесс интегрирующего звена. На практике сущ. интегрирующие звенья с замедлением. (Tp+1)y=kx/p, где (Tp+1) - замедление W (p)=к/(Tp+1). Пример - электродвигатель постоянного тока, у кот. в качестве выходной величины рассмат-ся угол поворота.
 или в операторной форме
или в операторной форме  . Передаточн. ф-ция
. Передаточн. ф-ция  . Ед. идеальным диф-щим звеном, кот. точно описывается ур-м, явл. тахогенератор постоян. тока (рис), если в качестве входн. величины рассм-ть угол поворота его ротора a, а в качестве вых. – напряж. якоря U.
. Ед. идеальным диф-щим звеном, кот. точно описывается ур-м, явл. тахогенератор постоян. тока (рис), если в качестве входн. величины рассм-ть угол поворота его ротора a, а в качестве вых. – напряж. якоря U.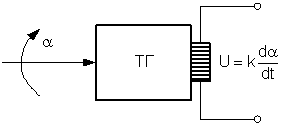
 . Передат. ф-ция звена
. Передат. ф-ция звена  . Звено условно можно представить в виде двух включенных последовательно звеньев – идеальн. диф. звена и апериодич. звена первого порядка. Рис. диф. RC-цепь (а), RL-цепь (б) и диф-щий трансформатор (в).
. Звено условно можно представить в виде двух включенных последовательно звеньев – идеальн. диф. звена и апериодич. звена первого порядка. Рис. диф. RC-цепь (а), RL-цепь (б) и диф-щий трансформатор (в).




 Для выч. запаса устойчивости по амплитуде необходимо по любому из критериев устойчивости опр-ть kгр. При вычислении запаса устойчивости по фазе нужно вначале опр. частоту среза из ур-ния
Для выч. запаса устойчивости по амплитуде необходимо по любому из критериев устойчивости опр-ть kгр. При вычислении запаса устойчивости по фазе нужно вначале опр. частоту среза из ур-ния 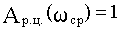 и затем найти
и затем найти  . Запас устойчивости по фазе будет равен:
. Запас устойчивости по фазе будет равен:  При наличии частотных характеристик запасы устойчивости отсчитываются прямо с графиков. Помимо логарифмических характеристик, с этой же целью можно использовать и АФЧХ (разомкнутой цепи), что проиллюстрировано на рис2. Для определения запаса уст-ти по фазе нужно провести луч из начала коор-т через точку АФЧХ, для кот. выполняется условие
При наличии частотных характеристик запасы устойчивости отсчитываются прямо с графиков. Помимо логарифмических характеристик, с этой же целью можно использовать и АФЧХ (разомкнутой цепи), что проиллюстрировано на рис2. Для определения запаса уст-ти по фазе нужно провести луч из начала коор-т через точку АФЧХ, для кот. выполняется условие  . Для нахождения этой точки графически следует провести R=1. Угол и будет ∆φ. Запас устойчивости по амплитуде хар-т удаленность точки АФЧХ
. Для нахождения этой точки графически следует провести R=1. Угол и будет ∆φ. Запас устойчивости по амплитуде хар-т удаленность точки АФЧХ  от границы устойчивости, т.е. от точки с координатами - 1,j0. Следовательно,
от границы устойчивости, т.е. от точки с координатами - 1,j0. Следовательно,