
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий устойчивости МихайловаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Российский ученым. Критерий Михайлова предполагает построение годографа на комплексной плоскости. Для построения годографа исп. характер-кое ур-ние замкнутой с-мы путем подстановки p=jω получают аналитич. выражение вектора M(jω): M(jω)=a0(jω)n+a1(jω)n-1+...+an. Кот. явл. комплексным и может быть представлено в виде:
Построение годографа производится по уравнению вектора M(jω) при изменении часты от 0 до + Критерий Михайлова: система устойчива, если годограф Михайлова M(jω) при изменении от 0 до +
Характеристические кривые (АФЧХ) систем: устойчивых (а), на границе устойчивости (б), не устойчивых (в) Критерий устойчивости Найквиста Данный критерий позволяет по амплитудно-фазовой частотной характеристике разомкнутой системы оценить устойчивость системы. Он позволяет определить устойчивость замкнутой системы по виду АФЧХ системы в разомкнутом состоянии. Различают формулировка критерия для случаев, когда система в разомкнутом состоянии устойчива и неустойчива. В первом случае критерий устойчивости формулируются так: САУ, которая устойчива в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если АФЧХ разомкнутой системы не охватывает точку на комплексной плоскости с координатами (-1, j0).
Передаточн. функция разомкнутой с-мы:
Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин: Помимо исследования устойчивости, можно оценить и некоторые качественные показатели замкнутой системы, например, запас устойчивости. Запасы устойчивости При оценке устойчивости САУ одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т.е. степени удаленности с-мы от границы устойчивости. Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины - запас устойчивости по фазе ∆φ и запас устойчивости по амплитуде ∆G (рис 1).
Запас устойчивости по фазе определяется величиной ∆φ, на кот. должно возрасти запаздывание по фазе в с-ме с частотой среза, чтобы с-ма оказалась на границе устойчивости. Запас устойчивости по амплитуде опр. величиной ∆G допустимого подъема ЛАЧХ, при кот. с-ма окажется на границе устойчивости. Т.е., запас по амплитуде представляет собой запас по коэф. передачи разомкнутой цепи по отношению к его граничному по устойчивости значению:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.235.195 (0.005 с.) |


 . Оценка устойчивости системы осущ. по углу поворота годографа при изменении частоты 0<ω<
. Оценка устойчивости системы осущ. по углу поворота годографа при изменении частоты 0<ω<  , т.к. m=0 для обеспечения устойчивости с-мы.
, т.к. m=0 для обеспечения устойчивости с-мы.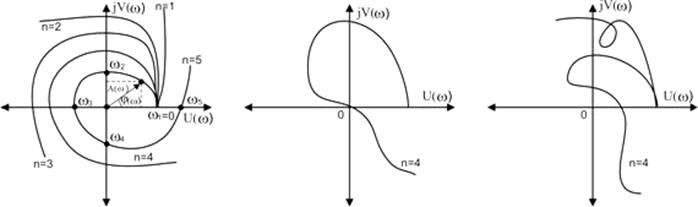


 и ф-ция разомкнутой системы:
и ф-ция разомкнутой системы: 
 .
.

 Для выч. запаса устойчивости по амплитуде необходимо по любому из критериев устойчивости опр-ть kгр. При вычислении запаса устойчивости по фазе нужно вначале опр. частоту среза из ур-ния
Для выч. запаса устойчивости по амплитуде необходимо по любому из критериев устойчивости опр-ть kгр. При вычислении запаса устойчивости по фазе нужно вначале опр. частоту среза из ур-ния 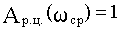 и затем найти
и затем найти  . Запас устойчивости по фазе будет равен:
. Запас устойчивости по фазе будет равен:  При наличии частотных характеристик запасы устойчивости отсчитываются прямо с графиков. Помимо логарифмических характеристик, с этой же целью можно использовать и АФЧХ (разомкнутой цепи), что проиллюстрировано на рис2. Для определения запаса уст-ти по фазе нужно провести луч из начала коор-т через точку АФЧХ, для кот. выполняется условие
При наличии частотных характеристик запасы устойчивости отсчитываются прямо с графиков. Помимо логарифмических характеристик, с этой же целью можно использовать и АФЧХ (разомкнутой цепи), что проиллюстрировано на рис2. Для определения запаса уст-ти по фазе нужно провести луч из начала коор-т через точку АФЧХ, для кот. выполняется условие  . Для нахождения этой точки графически следует провести R=1. Угол и будет ∆φ. Запас устойчивости по амплитуде хар-т удаленность точки АФЧХ
. Для нахождения этой точки графически следует провести R=1. Угол и будет ∆φ. Запас устойчивости по амплитуде хар-т удаленность точки АФЧХ  от границы устойчивости, т.е. от точки с координатами - 1,j0. Следовательно,
от границы устойчивости, т.е. от точки с координатами - 1,j0. Следовательно, 



