
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка устойчивости сау по логарифмическим частотным характеристикам. Запасы устойчивостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В соответствии с критерием Найквиста об устойчивости можно судить не только по АФЧХ, но и совместно по амплитудной и фазовой частотным характеристикам разомкнутой цепи. Обычно при этом пользуются логарифмическими характеристиками, что представляет большое удобство в силу простоты их построения. Но если ЛАЧХ используется асимптотическая, то расчеты будут достаточно грубыми. Если АФЧХ не охватывает точку Однако На рис. 4.12 для ЛАЧХ, показанной сплошной линией, это неравенство соблюдается Возможен и более сложный случай. Как было показано в примере 4.4, САУ устойчива при
Рис. 4.12 — Оценка устойчивости САУ по ЛАЧХ и ЛФЧХ
Рис. 4.13 — Варианты ЛАЧХ и ЛФЧХ для условно устойчивой САУ Эта ситуация характерна для условно устойчивых систем, и для них оценка устойчивости по логарифмическим частотным характеристикам выглядит по-другому: система будет устойчивой, если все частоты переворота фазы больше частоты среза или если ее ЛФЧХ до частоты среза принимает значение При оценке устойчивости САУ одного факта устойчивости недостаточно. Необходимо еще оценить величину запаса устойчивости, т.е. степени удаленности системы от границы устойчивости. Основное распространение в качестве меры запаса устойчивости получили вытекающие из критерия Найквиста две величины — запас устойчивости по фазе Запас устойчивости по амплитуде
Оценку запаса устойчивости САУ по амплитуде можно также провести, зная частоту переворота фазы
Таким образом, для определения запаса устойчивости по амплитуде необходимо либо по любому из критериев устойчивости рассчитать Запас устойчивости по фазе определяется величиной При вычислении запаса устойчивости по фазе нужно вначале определить частоту среза из уравнения
При наличии логарифмических частотных характеристик запасы устойчивости отсчитываются прямо с графиков, например как показано на рис. 4.14, а.
Рис. 4.14 — Запасы устойчивости САУ на логарифмических частотных характеристиках (а) и на АФЧХ (б)
Помимо ЛАЧХ и ЛФЧХ, с этой же целью можно использовать и АФЧХ (разомкнутой цепи), что проиллюстрировано на рис. 4.14, б. Для определения запаса устойчивости по фазе нужно провести радиус-вектор из начала координат через точку АФЧХ, для которой выполняется условие Запас устойчивости по амплитуде характеризует удаленность точки АФЧХ
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.107.215 (0.01 с.) |

 , то при частоте, на которой
, то при частоте, на которой 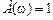 , абсолютное значение фазы больше
, абсолютное значение фазы больше 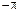 . Но значение
. Но значение  соответствует
соответствует  . Поэтому для устойчивости замкнутой САУ необходимо, чтобы ЛАЧХ разомкнутой цепи пересекла ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение –p.
. Поэтому для устойчивости замкнутой САУ необходимо, чтобы ЛАЧХ разомкнутой цепи пересекла ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение –p. на частоте среза
на частоте среза 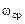 , а
, а  на частоте переворота фазы
на частоте переворота фазы  . Следовательно, система будет абсолютно устойчива, если
. Следовательно, система будет абсолютно устойчива, если  .
.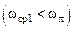 , значит, САУ устойчива,
, значит, САУ устойчива,  . При увеличении коэффициента передачи
. При увеличении коэффициента передачи  ЛАЧХ смещается вверх и на границе устойчивости (пунктирная кривая) при
ЛАЧХ смещается вверх и на границе устойчивости (пунктирная кривая) при  частоты
частоты  и
и  приводит к неустойчивости системы, тогда
приводит к неустойчивости системы, тогда  (штрихпунктирная кривая).
(штрихпунктирная кривая). с–1. При этом ее АФЧХ будет дважды пересекать отрицательную вещественную полуось, как показано на рис. 4.10, а, при частотах
с–1. При этом ее АФЧХ будет дважды пересекать отрицательную вещественную полуось, как показано на рис. 4.10, а, при частотах  и
и  . ЛАЧХ такой системы изображена сплошной линией на рис. 4.13, и ее частота среза
. ЛАЧХ такой системы изображена сплошной линией на рис. 4.13, и ее частота среза  меньше любой из частот
меньше любой из частот  и
и  . При
. При  с–1 частота среза
с–1 частота среза  (на рис. 4.13 ЛАЧХ показана пунктирной линией) и САУ становится неустойчивой. При
(на рис. 4.13 ЛАЧХ показана пунктирной линией) и САУ становится неустойчивой. При  с–1 САУ снова станет устойчивой, хотя частота среза
с–1 САУ снова станет устойчивой, хотя частота среза  (ЛАЧХ изображена штрихпунктирной линией на рис. 4.13) больше частот
(ЛАЧХ изображена штрихпунктирной линией на рис. 4.13) больше частот 

 и запас устойчивости по амплитуде
и запас устойчивости по амплитуде 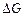 .
. (4.9)
(4.9) , тогда
, тогда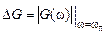 . (4.10)
. (4.10) и воспользоваться далее формулой (4.9), либо вычислить частоту
и воспользоваться далее формулой (4.9), либо вычислить частоту  и затем найти
и затем найти  . Тогда запас устойчивости по фазе, вычисленный в градусах, будет равен
. Тогда запас устойчивости по фазе, вычисленный в градусах, будет равен .
.
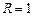 . Угол между этим лучом и отрицательной действительной полуосью и будет
. Угол между этим лучом и отрицательной действительной полуосью и будет  от границы устойчивости, т.е. от точки с координатами
от границы устойчивости, т.е. от точки с координатами  (
( .
.


