
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие устойчивости линейных непрерывных САУСодержание книги
Поиск на нашем сайте
Система называется устойчивой: – если после снятия воздействия по окончании переходного процесса возвращается в исходное равновесное состояние; – после изменения воздействия на постоянную величину по окончании переходного процесса приходит в новое равновесное состояние. Определим условия устойчивости. Пусть передаточная функция замкнутой по какому-либо из воздействий САУ имеет вид
где Именно свободная составляющая и определяет переходный процесс в системе. В общем случае полюсы являются комплексными. При этом они образуют пары сопряженных чисел:
где При этом, если Отсюда следует, что общим условием затухания всех составляющих, а значит, и всего переходного процесса в целом является отрицательность вещественных частей всех полюсов передаточной функции САУ. Если хотя бы один полюс имеет положительную вещественную часть, переходный процесс будет расходящимся и система будет неустойчивой. Изображая полюсы передаточной функции САУ (корни ее характеристического уравнения) точками на комплексной плоскости, как показано на рис. 4.2, условие устойчивости можно сформулировать еще так: необходимым и достаточным условием устойчивости САУ является расположение всех полюсов ее передаточной функции (корней характеристического уравнения) в левой комплексной полуплоскости. Мнимая ось плоскости корней служит границей устойчивости. При этом можно выделить три случая выхода САУ на границу устойчивости, которые характеризуются соответственно: – нулевым полюсом – парой чисто мнимых полюсов – бесконечно удаленным полюсом Бесконечность на комплексной плоскости рассматривается как бесконечно удаленная точка, противоположная нулевой. Поэтому она тоже является границей между правой и левой полуплоскостями.
Рис. 4.2 — Расположение полюсов передаточной функции устойчивой САУ на комплексной плоскости
Вычисление корней весьма просто лишь для характеристического уравнения первой и второй степени. Но ведь для определения устойчивости не нужно знать абсолютное значение корней, необходимо знать лишь, в какой полуплоскости они находятся. Поэтому важное значение приобретают правила, позволяющие определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости. К основным критериям устойчивости относятся алгебраический критерий Гурвица и частотные критерии Михайлова и Найквиста.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.140.82 (0.009 с.) |

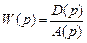 , причем она имеет только
, причем она имеет только 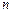 простых полюсов (корней характеристического уравнения
простых полюсов (корней характеристического уравнения  ). Подадим на вход САУ единичное ступенчатое воздействие амплитудой
). Подадим на вход САУ единичное ступенчатое воздействие амплитудой 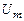 , тогда, в соответствии с формулой (2.14), изменение выходной величины
, тогда, в соответствии с формулой (2.14), изменение выходной величины  будет описываться выражением
будет описываться выражением ,
, — установившаяся (вынужденная) составляющая, однозначно связанная с изменением входной величины (частное решение неоднородного дифференциального уравнения с правой частью);
— установившаяся (вынужденная) составляющая, однозначно связанная с изменением входной величины (частное решение неоднородного дифференциального уравнения с правой частью); 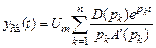 — свободная составляющая, изменяющаяся во времени в течение переходного процесса (определяется общим решением однородного дифференциального уравнения
— свободная составляющая, изменяющаяся во времени в течение переходного процесса (определяется общим решением однородного дифференциального уравнения 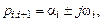
 может быть положительной или отрицательной величиной.
может быть положительной или отрицательной величиной. , эта составляющая будет затухать. Наоборот, при
, эта составляющая будет затухать. Наоборот, при  получатся расходящиеся колебания.
получатся расходящиеся колебания.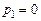 ;
;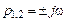 ;
; .
.



