
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные функции и характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальные (гармонические) колебания с постоянными амплитудой и частотой Таким образом, при подаче на вход системы гармонических колебаний с постоянной амплитудой, но c различными частотами на выходе системы получаются также гармонические колебания с теми же частотами, но различными амплитудами и фазами относительно входных колебаний. Известно, что для оригинала
где Сравнивая формулу (2.10) с формулой прямого преобразования Лапласа Поскольку
Функция комплексного переменного Годограф функции
Рис. 2.8 — Годограф АФЧХ и другие частотные характеристики
Как и всякую функцию комплексного переменного, функцию
где Все величины, представленные в (2.12), являются соответствующими частотными функциями, а построенные по выражениям для функций графики — частотными характеристиками. Зависимости Зависимость Зависимость Между всеми частотными характеристиками существует непосредственная связь, вытекающая из тригонометрических соотношений и поясняемая рис. 2.8.
В практических расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ. Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом величины отношения мощности на выходе
Но так как бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1 Б), то за единицу измерения ее принят децибел, 1дБ = 0,1 Б. С учетом этого можно записать:
Величина логарифма амплитудной частотной характеристики, выраженная в децибелах
называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз — на 40 дБ, в 1000 раз — на 60 дБ и т.д. Вычислим, какому отношению амплитуд соответствует один децибел, два и т.д.
то есть 1 дБ 2 дБ 3 дБ Фазовая частотная характеристика Единицей измерения частоты является логарифмическая единица — декада. Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением. В логарифмическом масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину, равную
ЛАЧХ и ЛФЧХ строят обычно совместно, используя общую ось абсцисс (ось частот). Начало координат невозможно взять в точке Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза Из рассмотренных здесь частотных характеристик две можно получить экспериментально – амплитудную
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 695; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.202.168 (0.009 с.) |

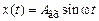 , то после затухания переходных процессов на выходе также возникают синусоидальные колебания
, то после затухания переходных процессов на выходе также возникают синусоидальные колебания 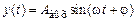 той же частоты, но другой амплитуды и сдвинутые по фазе относительно входных колебаний.
той же частоты, но другой амплитуды и сдвинутые по фазе относительно входных колебаний.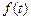 (а именно таковыми являются в САУ входные и выходные сигналы) имеет место одностороннее преобразование Фурье [2, 3], в соответствии с которым спектральная функция
(а именно таковыми являются в САУ входные и выходные сигналы) имеет место одностороннее преобразование Фурье [2, 3], в соответствии с которым спектральная функция 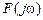 может быть рассчитана по формуле
может быть рассчитана по формуле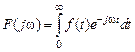 , (2.10)
, (2.10)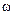 — угловая частота.
— угловая частота.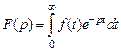 , легко видеть их идентичность, поэтому для перехода из области изображений в частотную область достаточно чисто формально в изображениях
, легко видеть их идентичность, поэтому для перехода из области изображений в частотную область достаточно чисто формально в изображениях 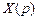 и
и 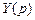 заменить оператор Лапласа
заменить оператор Лапласа 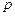 на переменную (оператор Фурье)
на переменную (оператор Фурье) 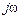 .
. , то в результате такой замены получим
, то в результате такой замены получим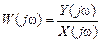 . (2.11)
. (2.11)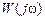 называется частотной передаточной функцией (в литературе ее также часто называют комплексным коэффициентом передачи). Она получается путем чисто формальной замены в выражении передаточной функции оператора Лапласа
называется частотной передаточной функцией (в литературе ее также часто называют комплексным коэффициентом передачи). Она получается путем чисто формальной замены в выражении передаточной функции оператора Лапласа 
 , (2.12)
, (2.12) и
и 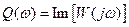 — действительная и мнимая части частотной передаточной функции,
— действительная и мнимая части частотной передаточной функции, 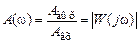 и
и 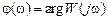 — модуль и аргумент частотной передаточной функции.
— модуль и аргумент частотной передаточной функции.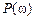 и
и  называются вещественной и мнимой частотными характеристиками соответственно.
называются вещественной и мнимой частотными характеристиками соответственно.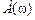 показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.
показывает отношение амплитуд выходного и входного гармонических сигналов при изменении частоты и называется амплитудной частотной характеристикой.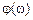 показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.
показывает сдвиг фазы выходного гармонического сигнала относительно входного при изменении частоты и называется фазовой частотной характеристикой.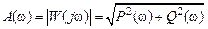 ,
,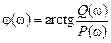 ,
, ,
, 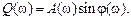
 к мощности на входе
к мощности на входе  в технике принят бел (Б). Так как мощность сигнала пропорциональна квадрату его амплитуды, получим:
в технике принят бел (Б). Так как мощность сигнала пропорциональна квадрату его амплитуды, получим: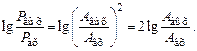


 ,
,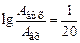 ,
, ,
,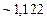 ,
,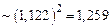 ,
,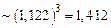 .
.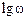 ), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).
), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).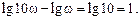
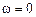 , так как
, так как 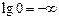 . Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.
. Поэтому начало координат можно брать в любой удобной точке в зависимости от интересующего диапазона частот.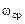 . Ось абсцисс соответствует значению
. Ось абсцисс соответствует значению 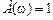 , то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).
, то есть прохождению амплитуды сигнала в натуральную величину (поэтому еще говорят, что на частоте среза система теряет усилительные свойства).


