
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирующее (идеальное) звеноСодержание книги
Поиск на нашем сайте
Уравнение и передаточная функция звена:
Выходная величина пропорциональна скорости изменения входной величины. Если входная и выходная величины имеют одинаковую размерность, то коэффициент Выражения для основных функций:
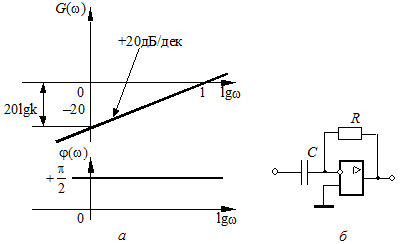
Как передаточная функция, так соответственно и частотные характеристики дифференцирующего звена являются обратными передаточной функции и соответствующим характеристикам интегрирующего звена. Логарифмические частотные характеристики рассматриваемого звена приведены на рис. 3.2, а.
Рис. 3.2 — Частотные характеристики дифференцирующего звена (а) и его реализация на операционном усилителе (б)
При построении ЛАЧХ удобно отложить точку с координатами О том, что звено с представленным математическим описанием является идеальным, говорит, к примеру, переходная функция. Ни в каком реальном устройстве невозможно получить мгновенный скачек выходной величины бесконечной амплитуды. Реальные дифференцирующие звенья обладают конечной инерционностью, вследствие чего осуществляемое ими дифференцирование не является точным. На рис. 3.2, б изображен вариант реализации дифференцирующего звена на операционном усилителе с конденсатором
Неидеальность реализации звена определена напряжением питания усилителя, его выходное напряжение будет конечной величиной.
3.2.1.4 Инерционное звено (апериодическое звено первого порядка)
Описывается дифференциальным уравнением
Перейдя к изображениям, получим:
Передаточные и частотные функции:
На рис. 3.3 приведены основные частотные характеристики инерционного звена. Годограф АФЧХ (рис. 3.3, а) имеет вид полуокружности радиуса
ЛАЧХ звена показана на рис. 3.3, в. Но эта же характеристика может быть представлена приближенно ломаной линией, которая показана на том же рисунке. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится ЛАЧХ при w ® 0 и w ® ¥. При малых значениях w можно считать С другой стороны, на больших частотах
В этом случае характеристика представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении w на декаду, т.е. в 10 раз,
Таким образом, величина Максимальное расхождение между точной (
От параметров звена рассматриваемая величина не зависит. На этом же рисунке показана ЛФЧХ: при w ® ¥ значение j изменяется от 0 до минус Переходная функция инерционного звена может быть выведена по формуле (2.14). Если
а импульсная переходная функция
Переходная и импульсная переходная характеристики представлены на рис. 3.4, а, б.
и его реализация на операционном усилителе (в)
Динамические свойства звена характеризуются постоянной времени
В рассмотренных выше примерах по определению передаточных функций схемы на рис. 2.3, 2.4, 2.7, а являются инерционными (апериодическими) звеньями. Реализация этого звена на операционном усилителе приведена на рис. 3.4, в. Действительно, если
то где
Пример 3.1 Асимптотическая ЛАЧХ апериодического звена имеет частоту среза Нужно на графике или мысленно провести из точки на оси частот
Форсирующее звено Часто в литературе это звено именуется как пропорционально-дифференцирующее. Выходная величина этого звена пропорциональна входной и производной от входной величины. Передаточная функция и основные частотные функции:
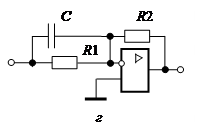
Звено характеризуется двумя параметрами — коэффициентом передачи На рис. 3.5, а — в приведены частотные характеристики форсирующего звена, они являются обратными характеристикам инерционного звена. АФЧХ (рис. 3.5, а) имеет вид вертикальной прямой, расположенной в первом квадранте комплексной плоскости на расстоянии На рис. 3.5, г приведена схемная реализация форсирующего звена на операционном усилителе (на пассивных четырехполюсниках это звено не реализуется). Поскольку в схеме
то где
Рис. 3.5 — Частотные характеристики форсирующего звена (а — в) и его реализация на операционном усилителе (г) Переходная характеристика форсирующего звена Остальные звенья первого порядка образованы путем последовательного соединения рассмотренных звеньев, и их относят к типовым ввиду широкого применения в САУ.
|
||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 757; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.69.58 (0.01 с.) |

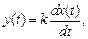
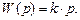
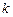 измеряется в секундах. В этом случае его принято обозначать через
измеряется в секундах. В этом случае его принято обозначать через  и называть постоянной времени дифференцирующего звена.
и называть постоянной времени дифференцирующего звена.
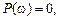
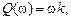

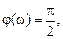
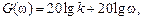
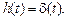

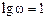 , провести через нее прямую с наклоном плюс 20 дБ/дек, затем отложить на оси
, провести через нее прямую с наклоном плюс 20 дБ/дек, затем отложить на оси  отрезок
отрезок 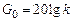 (поскольку, как правило,
(поскольку, как правило, 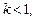 точка
точка  будет находиться ниже оси
будет находиться ниже оси 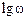 ) и провести параллельную прямую.
) и провести параллельную прямую.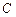 во входной цепи и резистором
во входной цепи и резистором 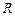 в цепи обратной связи. Тогда
в цепи обратной связи. Тогда ,
,  ,
, .
.
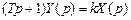 .
.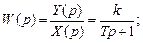
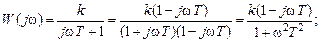
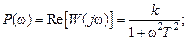
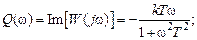

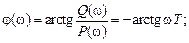
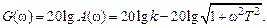
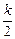 с центром в точке
с центром в точке 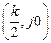 , расположенной в четвертом квадранте комплексной плоскости. АЧХ (рис. 3.3, б) монотонно уменьшается с ростом частоты, начиная со значения
, расположенной в четвертом квадранте комплексной плоскости. АЧХ (рис. 3.3, б) монотонно уменьшается с ростом частоты, начиная со значения 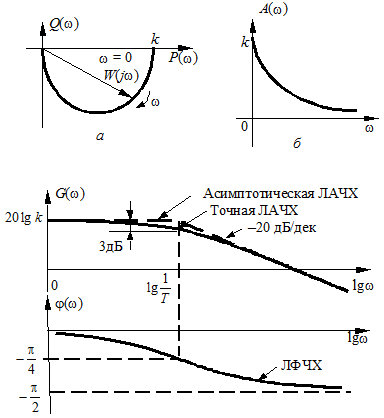 Рис. 3.3 — Частотные характеристики инерционного звена
Рис. 3.3 — Частотные характеристики инерционного звена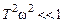 , то есть
, то есть 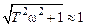 , следовательно,
, следовательно, 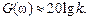 Соответственно характеристика представляет собой прямую, параллельную оси абсцисс и проходящую на уровне
Соответственно характеристика представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 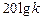 . Это первая асимптота, к которой стремится ЛАЧХ при w ® 0.
. Это первая асимптота, к которой стремится ЛАЧХ при w ® 0.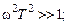
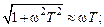

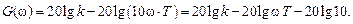
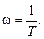 Поэтому эта частота называется частотой сопряжения (сопрягающей частотой).
Поэтому эта частота называется частотой сопряжения (сопрягающей частотой).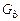 ) и асимптотической (
) и асимптотической (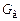 ) ЛАЧХ наблюдается при частоте сопряжения. Вычислим это расхождение, подставив в соотношения для
) ЛАЧХ наблюдается при частоте сопряжения. Вычислим это расхождение, подставив в соотношения для 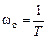 :
: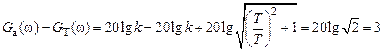 дБ.
дБ.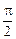 . При этом в точке
. При этом в точке 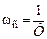 имеем
имеем  .
.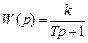 , то
, то 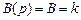 ,
,  ,
, 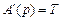 . Передаточная функция имеет один полюс
. Передаточная функция имеет один полюс 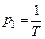 . Тогда по формуле (2.14) получим
. Тогда по формуле (2.14) получим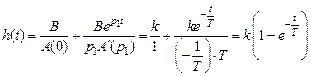 ,
,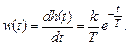
 Рис. 3.4 — Временные характеристики инерционного звена (а, б)
Рис. 3.4 — Временные характеристики инерционного звена (а, б) . Постоянная времени может быть определена как время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени (см. рис. 3.4, а). Коэффициент передачи
. Постоянная времени может быть определена как время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени (см. рис. 3.4, а). Коэффициент передачи  ,
, ,
,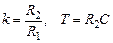 .
. . Частотой среза
. Частотой среза 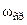 называется частота, при которой ЛАЧХ пересекает ось частот, т.е.
называется частота, при которой ЛАЧХ пересекает ось частот, т.е. 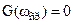 . Это означает, что частотный коэффициент передачи устройства или системы равен единице и при
. Это означает, что частотный коэффициент передачи устройства или системы равен единице и при  происходит усиление выходного сигнала, а при
происходит усиление выходного сигнала, а при  – его ослабление. Коэффициент передачи звена
– его ослабление. Коэффициент передачи звена 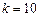 . Требуется определить постоянную времени
. Требуется определить постоянную времени 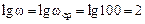 прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне
прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне 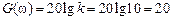 . Координата точки пересечения по оси частот даст логарифм сопрягающей частоты
. Координата точки пересечения по оси частот даст логарифм сопрягающей частоты 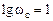 , отсюда
, отсюда 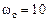 и
и 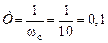 с.
с.
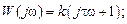
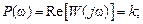
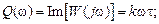
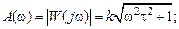

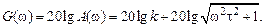
 от начала координат. АЧХ (рис. 3.5, б) монотонно возрастает с ростом частоты, начиная со значения
от начала координат. АЧХ (рис. 3.5, б) монотонно возрастает с ростом частоты, начиная со значения  . ЛФЧХ форсирующего звена точно такая же, как и у инерционного, только фаза имеет положительные значения.
. ЛФЧХ форсирующего звена точно такая же, как и у инерционного, только фаза имеет положительные значения. ,
,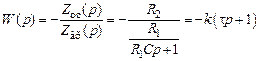 ,
,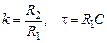 .
.
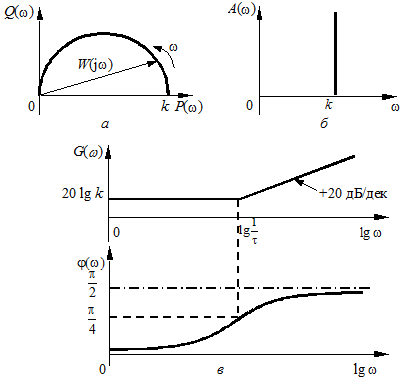
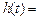
 , т.е. равна сумме переходных характеристик дифференцирующего и пропорционального звеньев. В начальный момент времени она имеет скачок бесконечной амплитуды, как и у идеального дифференцирующего звена, а далее проходит горизонтально, как и у пропорционального звена.
, т.е. равна сумме переходных характеристик дифференцирующего и пропорционального звеньев. В начальный момент времени она имеет скачок бесконечной амплитуды, как и у идеального дифференцирующего звена, а далее проходит горизонтально, как и у пропорционального звена.


