
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные критерии оценки качестваСодержание книги
Поиск на нашем сайте
Наибольшее распространение получили частотные критерии, в основу которых положено использование частотных характеристик САУ. Для иллюстрации возможности оценки качества переходного процесса по частотным характеристикам установим точную аналитическую зависимость между переходной характеристикой В качестве примера рассмотрим связь переходных характеристик САУ с вещественной частотной характеристикой Пусть на вход устойчивой САУ, передаточная функция которой
Если вещественная часть
Так как при
или
В окончательном виде оригинал запишется соотношением
Поскольку переходная функция САУ является интегралом от импульсной переходной функции, т.е.
Формула (5.8) представляет собой запись интеграла Фурье для четной функции в вещественной форме, поэтому, ввиду абсолютной интегрируемости функции
После вычисления внутреннего интеграла окончательно получим:
Пользуясь формулой (5.9), можно непосредственно или приближенно [4, 5] по ВЧХ замкнутой САУ рассчитать ее переходную характеристику. Также можно составить предварительное приближенное суждение о качестве по виду ВЧХ. Различные виды ВЧХ представлены на рис. 5.5.
Рис. 5.5 — Типы вещественных частотных характеристик САУ
Основные положения оценки качества переходного процесса по ВЧХ сводятся к следующему. 1. Установившееся значение 2. Двум ВЧХ, сходным по форме, но отличающимся масштабом по оси абсцисс в 3. Разрыв непрерывности на ВЧХ свидетельствует о том, что система находится на границе устойчивости. Разрыву при 4. Если ВЧХ непрерывна, положительна и имеет вид вогнутой кривой (кривая 1 на рис. 5.5), то переходная характеристика монотонна. 5. При положительной невозрастающей ВЧХ (кривая 2 на рис. 5.5) перерегулирование в системе не превышает 18 %, т.е. 6. При наличии у положительной ВЧХ максимума (величина
7. Если ВЧХ имеет положительный и отрицательный экстремумы (величины
8. Острый пик на ВЧХ на угловой частоте 9. Если ВЧХ непрерывная, невозрастающая и по форме приближается к трапецеидальной (рис. 5.6), то время переходного процесса можно определить по соотношению
Частота Следует отметить, что оценка перерегулирования по форме ВЧХ имеет весьма приблизительный характер. Реальное перерегулирование может быть в десятки раз меньше значений, рассчитанных по формулам (5.10), (5.11). Колебательность переходной характеристики можно оценить по величине относительного максимума амплитудной частотной характеристики (АЧХ)
качества по АЧХ
Величина относительного максимума называется показателем колебательности
где При Физический смысл этой оценки заключается в том, что она показывает максимально возможное отношение амплитуды выходной величины к амплитуде гармонического входного воздействия. Значение Показатель колебательности Вследствие предельной простоты построения ЛАЧХ удобно пользоваться именно этой характеристикой. Информацию здесь несет среднечастотная часть ЛАЧХ. На частоте среза
Здесь значение
Величины наклонов ЛАЧХ слева от Описанная методика оценки времени переходного процесса по ЛАЧХ применяется при синтезе последовательных корректирующих устройств, изложенном в разделе 6.
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.006 с.) |

 и частотными характеристиками САУ (ВЧХ, АЧХ, ЛАЧХ и т.д.).
и частотными характеристиками САУ (ВЧХ, АЧХ, ЛАЧХ и т.д.).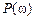 .
.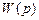 не содержит полюсов в правой полуплоскости, подано единичное ступенчатое воздействие
не содержит полюсов в правой полуплоскости, подано единичное ступенчатое воздействие 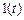 . Из этого следует, что импульсная переходная функция
. Из этого следует, что импульсная переходная функция  удовлетворяет условию абсолютной интегрируемости и может быть вычислена с помощью обратного преобразования Фурье по формуле
удовлетворяет условию абсолютной интегрируемости и может быть вычислена с помощью обратного преобразования Фурье по формуле .
.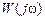 — четная функция, а мнимая часть
— четная функция, а мнимая часть  — нечетная функция, то получим
— нечетная функция, то получим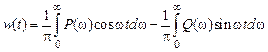 .
.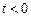 оригинал равен нулю и
оригинал равен нулю и  , то
, то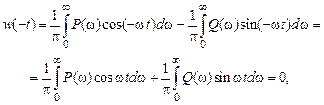
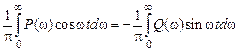 .
.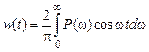 . (5.7)
. (5.7)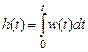 , то связь между переходной характеристикой САУ и ее ВЧХ находится путем подстановки формулы (5.7) в соотношение между двумя временными характеристиками:
, то связь между переходной характеристикой САУ и ее ВЧХ находится путем подстановки формулы (5.7) в соотношение между двумя временными характеристиками: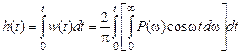 . (5.8)
. (5.8)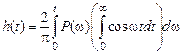 .
. . (5.9)
. (5.9)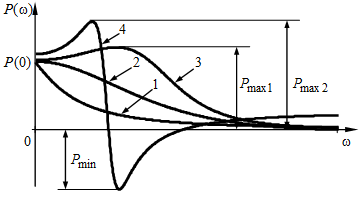
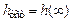 переходной характеристики определяется начальным значением ВЧХ
переходной характеристики определяется начальным значением ВЧХ  . Начальное значение
. Начальное значение 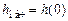 определяется конечным значением ВЧХ
определяется конечным значением ВЧХ  .
.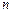 раз, соответствуют переходные характеристики, сходные по форме, но отличающиеся масштабом по оси абсцисс в
раз, соответствуют переходные характеристики, сходные по форме, но отличающиеся масштабом по оси абсцисс в  раз. Двум ВЧХ, сходным по форме, но отличающимся масштабом по оси ординат в
раз. Двум ВЧХ, сходным по форме, но отличающимся масштабом по оси ординат в 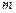 раз, соответствуют переходные характеристики, также сходные по форме, но отличающиеся масштабом по оси ординат в
раз, соответствуют переходные характеристики, также сходные по форме, но отличающиеся масштабом по оси ординат в 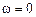 соответствует апериодическая граница устойчивости (наличие нулевого полюса в передаточной функции), а разрыву при
соответствует апериодическая граница устойчивости (наличие нулевого полюса в передаточной функции), а разрыву при 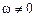 — колебательная граница устойчивости (наличие чисто мнимых полюсов в передаточной функции).
— колебательная граница устойчивости (наличие чисто мнимых полюсов в передаточной функции). %.
%. на кривой 3 рис. 5.5) перерегулирование в системе оценивается неравенством
на кривой 3 рис. 5.5) перерегулирование в системе оценивается неравенством . (5.10)
. (5.10)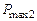 и
и 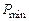 для кривой 4 на рис. 5.5), то перерегулирование в системе оценивается неравенством
для кривой 4 на рис. 5.5), то перерегулирование в системе оценивается неравенством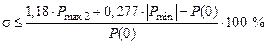 . (5.11)
. (5.11)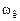 соответствует медленно затухающим колебаниям переходной характеристики с частотой, близкой к частоте
соответствует медленно затухающим колебаниям переходной характеристики с частотой, близкой к частоте 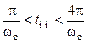 .
.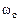 называется существенной частотой.
называется существенной частотой.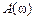 , примерный вид которой представлен на рис. 5.7.
, примерный вид которой представлен на рис. 5.7.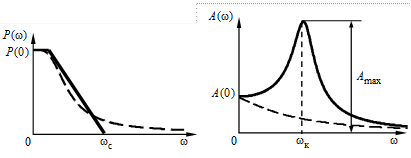 Рис. 5.6 — Трапецеидальная ВЧХ Рис. 5.7 — Определение показателей
Рис. 5.6 — Трапецеидальная ВЧХ Рис. 5.7 — Определение показателей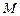 и определяется соотношением
и определяется соотношением ,
,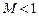 переходный процесс в САУ монотонный (пунктирная линия на рис. 5.7). Чем больше
переходный процесс в САУ монотонный (пунктирная линия на рис. 5.7). Чем больше 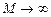 в системе имеют место незатухающие колебания.
в системе имеют место незатухающие колебания.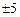 % от установившегося значения.
% от установившегося значения.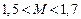 , хорошие запасы устойчивости, если
, хорошие запасы устойчивости, если  . Оптимальным обычно считается, если
. Оптимальным обычно считается, если  .
.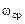 наклон ЛАЧХ должен составлять минус 20 дБ/дек, а значение
наклон ЛАЧХ должен составлять минус 20 дБ/дек, а значение 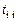 и перерегулированием
и перерегулированием  :
: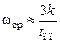 .
.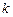 берется по графику, показанному на рис. 5.8, а в зависимости от величины перерегулирования
берется по графику, показанному на рис. 5.8, а в зависимости от величины перерегулирования  ,
, 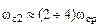 .
. Рис. 5.8 — Оценка времени переходного процесса по ЛАЧХ
Рис. 5.8 — Оценка времени переходного процесса по ЛАЧХ и справа от
и справа от 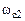 на качество переходного процесса почти не влияют.
на качество переходного процесса почти не влияют.


