
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальные характеристики сау. Настройка систем на технический и симметричный оптимумыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В ряде областей техники, например в многоконтурных системах электропривода с подчиненным регулированием, синтез последовательных корректирующих устройств осуществляется по-другому. Подчиненное регулирование предполагает независимость работы контуров системы. Так, например, в двухконтурной системе при работе внутреннего контура внешний отключен, и наоборот, если работает внешний контур, то отключается внутренний. Это возможно лишь в том случае, если каждый из контуров будет настроен на технический или симметричный оптимум. Считается [9, 10], что система будет иметь наилучшие (оптимальные) переходные процессы, если передаточная функция ее разомкнутой цепи будет иметь вид:
где Если для САУ имеет место (6.6), то говорят, что она настроена на технический оптимум (ТО). Известно [9, 10], что перерегулирование в САУ, для которой имеет место равенство (6.6), не превышает 5 %. Тогда, согласно номограммам Солодовникова, время переходного процесса можно оценить по соотношению:
На рис. 6.6 приведена ЛАЧХ для системы, настроенной на ТО. Так как частота среза
Рис. 6.6 — ЛАЧХ системы, настроенной на ТО
Из выражения (6.7) следует, что для САУ, настроенной на ТО, Если систему, настроенную на ТО, замкнуть инерционной обратной связью с коэффициентом передачи
На рис. 6.7 изображены переходные характеристики САУ, настроенной на ТО, при единичном входном воздействии,
Рис. 6.7 — Переходные характеристики САУ, настроенной на ТО, при различной инерционности цепи ее обратной связи
Из анализа приведенных переходных характеристик можно сделать следующие выводы: если
если если Поскольку отношение
Этим приемом пользуются при настройке на ТО многоконтурных систем, в частности электромеханических систем (ЭМС). Одна из задач настройки системы на ТО — сделать контур регулирования астатическим. Этого достичь не удается, если в состав объекта регулирования входит интегрирующее звено. Тогда стремятся получить передаточную функцию системы, ЛАЧХ которой на частоте среза сохраняет свойственный для ТО наклон –20 дБ/дек и меняет этот наклон до –40 дБ/дек в области низкой Одним из вариантов таких САУ являются системы, настроенные на симметричный оптимум (СО) [9, 10]. При этом передаточная функция разомкнутой цепи для САУ, обеспечивающих характеристики СО, имеет вид:
Известно [9, 10], что для системы, настроенной на СО, перерегулирование составляет около 43—45 %. Тогда, согласно номограммам Солодовникова, время переходного процесса можно оценить по соотношению:
На рис. 6.8 приведена ЛАЧХ для САУ, передаточная функция разомкнутой цепи которой представлена выражением (6.9). Для нее
Рис. 6.8 — ЛАЧХ системы, настроенной на СО
Следует отметить, что запас устойчивости по амплитуде Если САУ, настроенную на СО, замкнуть инерционной обратной связью с коэффициентом передачи
На рис. 6.9 приведены переходные характеристики САУ, настроенной на СО, при единичном входном воздействии,
Рис. 6.9 — Переходные характеристики САУ, настроенной на СО, при различной инерционности цепи ее обратной связи
Таким образом, постоянная времени в цепи обратной связи САУ, настроенной на какой-либо оптимум, приводит к увеличению перерегулирования, и при Обеспечение оптимальных показателей качества регулирования в динамических режимах (настройка САУ на ТО или СО) достигается в результате структурно-параметрического синтеза корректирующих устройств. Рассмотрим решение этой задачи на конкретном примере.
Пример 6.4 Произвести настройку внутреннего контура (рис. 6.10) двухконтурной САУ на технический оптимум при следующих параметрах:
Рис. 6.10 — Структурная схема внутреннего контура двухконтурной САУ
Передаточная функция разомкнутой цепи нескорректированной системы будет равна
Исходя из соотношения (6.7) определим значение эквивалентной некомпенсируемой постоянной времени
где При
Таким образом,
Отсюда передаточная функция корректирующего устройства
т.е. корректирующее устройство является ПИД-регулятором с передаточной функцией
Поскольку отношение Настройка САУ на симметричный оптимум производится аналогично. При этом для многоконтурной системы эквивалентная некомпенсируемая постоянная времени рассчитывается по формуле
Литература
1. Магазинников Л.И. Высшая математика III. Функции комплексного переменного. Ряды. Интегральные преобразования: Учеб. пособие. — Томск: Томск. гос. ун-т систем управления и радиоэлектроники, 1999. — 205 с. 2. Математические основы теории автоматического регулирования: В 2 т. / Под ред. проф. Б.К. Чемоданова. — М.: Высшая школа, 1977. 3. Г. Деч. Руководство к практическому применению преобразования Лапласа и 4. Теория автоматического управления: Учебник для вузов / Под ред. А.В. Нетушила. —2-е изд., доп. и перераб. — М.: Высшая школа, 1976. — 400 с. 5. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). —2-е изд., доп. и перераб. — М.: Машиностроение, 1982. — 504 с. 6. Попов Е.П. Теория линейных систем автоматического регулирования и управления. — М.: Наука, 1989. — 304 с. 7. Теория автоматического управления: В 2 ч. / Н.А. Бабаков и др.; под ред. А.А. Воронова. — М.: Высшая школа, 1986. — Ч.1: Теория линейных систем автоматического управления. — 367 с.
8. Юревич Е.И. Теория автоматического управления. — М.: Энергия, 1975. — 416 с. 9. Управление вентильными электроприводами постоянного тока / Е.Д. Лебедев, В.Е. Неймарк, М.Я. Пистарк, О.В. Слежановский. — М.: Энергия, 1970. — 198 с. 10. Москаленко В. В. Теория электропривода. — М.: Высшая школа, 1991. — 392 с. 11. Цыпкин Я.З. Теория импульсных систем. — М.: ГИФМЛ, 1958. — 724 с. 12. Э. Джури. Импульсные системы автоматического регулирования. — М.: ГИФМЛ, 1963. — 455 с. 13. Сигалов Г.Г., Мадорский Л.С. Основы теории дискретных систем управления. — Минск: «Вышэйш. школа», 1973. — 336 с. 14. Иванов В.А., Ющенко А.С. Теория дискретных систем автоматического управления. — М.: Наука, 1983. — 336 с. 15. Ерофеев А.А. Теория автоматического управления: Учебник для вузов. — 2-е изд., перераб. и доп. — СПб.: Политехника, 2002. — 302 с. 16. Теория автоматического управления: Учебник для вузов / С.В. Душин, Н.С. Зотов, Д.Х. Имаев и др.; под ред. В.Б. Яковлева. — 2-е изд., перераб. — М.: Высшая школа, 2005. — 567 с. 17. Мирошник И.В. Теория автоматического управления. Линейные системы. — СПб.: Питер, 2005. — 336 с. — (Серия «Учебное пособие»).
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.152 (0.013 с.) |

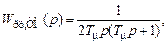 (6.6)
(6.6)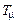 — эквивалентная некомпенсируемая постоянная времени САУ.
— эквивалентная некомпенсируемая постоянная времени САУ. .
. , то
, то . (6.7)
. (6.7)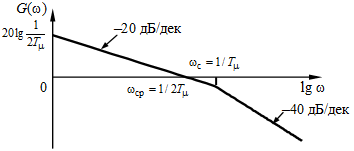
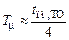 .
.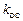 и постоянной времени
и постоянной времени 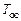 , то ее передаточная функция будет иметь вид
, то ее передаточная функция будет иметь вид .
.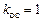 ,
, 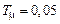 с и различных значениях
с и различных значениях  (кривая 1) перерегулирование составляет около 6,7 %, при
(кривая 1) перерегулирование составляет около 6,7 %, при 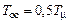 (кривая 2) — около 4,9 %, при
(кривая 2) — около 4,9 %, при 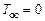 (кривая 3) — около 4,3 %. При этом время переходного процесса
(кривая 3) — около 4,3 %. При этом время переходного процесса 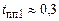 с при
с при 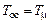 ,
, 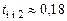 с при
с при 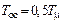 ,
, 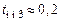 с при
с при 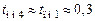 с.
с.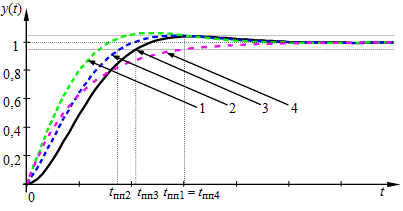
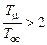 , то перерегулирование превышает 5 % и время переходного процесса увеличивается примерно в 1,5 раза по сравнению с расчетным
, то перерегулирование превышает 5 % и время переходного процесса увеличивается примерно в 1,5 раза по сравнению с расчетным 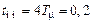 с;
с; , то перерегулирование не превышает 5 % и время переходного процесса уменьшается по сравнению с расчетным;
, то перерегулирование не превышает 5 % и время переходного процесса уменьшается по сравнению с расчетным;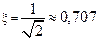 , время переходного процесса совпадает с расчетным.
, время переходного процесса совпадает с расчетным.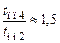 , иногда САУ, настроенную на ТО, приближенно эквивалентируют инерционным звеном, то есть
, иногда САУ, настроенную на ТО, приближенно эквивалентируют инерционным звеном, то есть . (6.8)
. (6.8)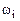 и высокой
и высокой 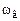 частот пропускания, отличающихся от частоты среза
частот пропускания, отличающихся от частоты среза 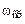 не менее чем в два раза.
не менее чем в два раза.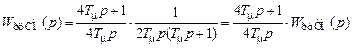 . (6.9)
. (6.9) . (6.10)
. (6.10) ,
,  и
и 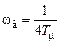 , поэтому, в соответствии с (6.10),
, поэтому, в соответствии с (6.10), ,
,
 . (6.11)
. (6.11)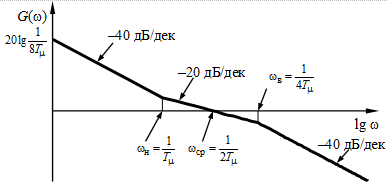
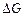 для систем, настроенных на ТО или СО, равен бесконечности, т.к. их фазовые характеристики никогда не достигают значения –180°. Запасы устойчивости по фазе соответственно равны
для систем, настроенных на ТО или СО, равен бесконечности, т.к. их фазовые характеристики никогда не достигают значения –180°. Запасы устойчивости по фазе соответственно равны 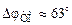 и
и 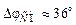 .
.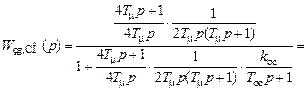
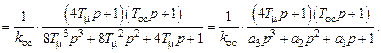
 с при
с при  с при
с при 
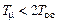 существенно снижается быстродействие САУ.
существенно снижается быстродействие САУ.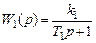 ,
, 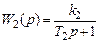 ,
, 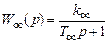 , где
, где  ,
, 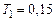 с,
с,  с,
с,  с. При этом необходимо обеспечить время переходного процесса
с. При этом необходимо обеспечить время переходного процесса 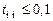 с.
с.
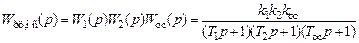 .
. ,
,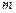 — общее количество контуров регулирования.
— общее количество контуров регулирования.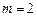 получим
получим с.
с.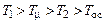 , и в качестве эквивалентной некомпенсируемой постоянной времени выбираем ближайшую к расчетному значению
, и в качестве эквивалентной некомпенсируемой постоянной времени выбираем ближайшую к расчетному значению 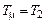 . Тогда для САУ, настроенной на ТО, в соответствии с (6.6) будем иметь
. Тогда для САУ, настроенной на ТО, в соответствии с (6.6) будем иметь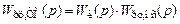 ,
, .
. ,
,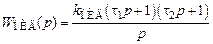 , у которого
, у которого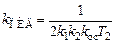 ,
, 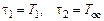 .
. , то переходная характеристика замкнутой скорректированной САУ будет иметь вид, близкий к кривой 2 на рис. 6.9, перерегулирование не превысит 5 % и заданное быстродействие системы будет обеспечено.
, то переходная характеристика замкнутой скорректированной САУ будет иметь вид, близкий к кривой 2 на рис. 6.9, перерегулирование не превысит 5 % и заданное быстродействие системы будет обеспечено.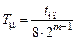 , а корректирующее устройство будет более сложным и, как правило, состоит из нескольких последовательно соединенных типовых регуляторов (см. подраздел 6.1).
, а корректирующее устройство будет более сложным и, как правило, состоит из нескольких последовательно соединенных типовых регуляторов (см. подраздел 6.1). -преобразования. — М.: ГИФМЛ, 1971. — 288 с.
-преобразования. — М.: ГИФМЛ, 1971. — 288 с.


