
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий устойчивости НайквистаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Критерий устойчивости Найквиста позволяет оценить устойчивость замкнутой САУ по ее разомкнутой цепи. Для этого в передаточной функции Если разомкнутая цепь устойчива (а это всегда имеет место, если САУ не содержит неустойчивых неминимально-фазовых звеньев), то формулировка критерия Найквиста звучит следующим образом. Для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф Найквиста при изменении На рис. 4.10 изображены основные из возможных ситуаций прохождения годографа Найквиста на комплексной плоскости. Сплошная кривая 1 на рис. 4.10, а соответствует абсолютно устойчивой замкнутой САУ (системе, которая остается устойчивой при уменьшении коэффициента передачи разомкнутой цепи), а пунктирная кривая 2 — условно устойчивой САУ (системе, устойчивой только в некотором диапазоне изменения коэффициента передачи разомкнутой цепи, как это было в примере 4.4). Сплошная кривая 3 на рис. 4.3, б проходит через критическую точку с координатами Физический смысл критерия Найквиста заключается в том, что при увеличении частоты входного воздействия сигнал, проходящий по цепи обратной связи, оказывается в противофазе с входным. Это равносильно замене отрицательной обратной связи на положительную. Если же при этой частоте разомкнутый контур обладает усилением (т.е.
неустойчивой САУ и САУ на границе устойчивости (б)
Для аналитических расчетов с помощью критерия Найквиста условия нахождения системы на границе устойчивости можно записать, используя вещественную и мнимую частотные функции разомкнутой цепи:
где При решении практических задач для оценки устойчивости САУ не обязательно строить годограф Найквиста, достаточно в частотной передаточной функции разомкнутой цепи Несмотря на наглядность критерия Найквиста и его физическую прозрачность, он имеет один существенный технический недостаток — вычислительные трудности, возникающие при разделении вещественной и мнимой частей
Пример 4.5 По критерию Найквиста получить выражение для оценки устойчивости и определить граничный коэффициент передачи для САУ, изображенной на рис. 4.3. В примере 4.1 была получена передаточная функция разомкнутой цепи
Произведем в
По правилам деления комплексных чисел [1] числитель и знаменатель полученного выражения нужно умножить на комплексную сопряженную функцию
Выразив из первого уравнения квадрат частоты
При На границе устойчивости
отсюда
Зададимся конкретными значениями коэффициентов передачи и постоянных времени. Пусть
Критерий Найквиста позволяет оценить устойчивость САУ, содержащих звенья чистого запаздывания. Пусть звено чистого запаздывания с передаточной функцией Результирующие передаточная и частотная передаточная функции разомкнутой цепи будут иметь вид
Поскольку
Таким образом, звено чистого запаздывания вносит лишь дополнительный фазовый сдвиг. При этом изменяется АФЧХ, т.е. меняются условия устойчивости (характеристика «закручивается» по часовой стрелке). При некотором По АФЧХ системы без запаздывания можно определить граничное (предельное) значение запаздывания Пусть АФЧХ устойчивой САУ без запаздывания
Рис. 4.11 — Определение граничного запаздывания
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 476; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.253.198 (0.012 с.) |

 производят замену оператора
производят замену оператора 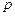 на переменную
на переменную 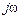 и на комплексной плоскости при изменении частоты от нуля (если это возможно) до бесконечности строят АФЧХ
и на комплексной плоскости при изменении частоты от нуля (если это возможно) до бесконечности строят АФЧХ 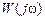 (годограф Найквиста).
(годограф Найквиста).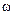 от 0 до
от 0 до 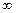 не охватывал точку с координатами
не охватывал точку с координатами  .
. ), то замкнутая САУ становится неустойчивой (любое увеличение сигнала на выходе приводит к увеличению сигнала на входе по цепи обратной связи, что вызывает дальнейший рост выходного сигнала и т.д.).
), то замкнутая САУ становится неустойчивой (любое увеличение сигнала на выходе приводит к увеличению сигнала на входе по цепи обратной связи, что вызывает дальнейший рост выходного сигнала и т.д.). Рис. 4.10 — Варианты годографа Найквиста для устойчивой (а),
Рис. 4.10 — Варианты годографа Найквиста для устойчивой (а), (4.8)
(4.8) — частота, соответствующая повороту радиус-вектора АФЧХ разомкнутой цепи на угол
— частота, соответствующая повороту радиус-вектора АФЧХ разомкнутой цепи на угол 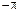 , т.е. до совпадения с отрицательной вещественной полуосью; ее называют частотой переворота фазы.
, т.е. до совпадения с отрицательной вещественной полуосью; ее называют частотой переворота фазы. , то система устойчива, в противном случае — неустойчива.
, то система устойчива, в противном случае — неустойчива.
 замену оператора
замену оператора 

 . Однако поскольку при определении частоты переворота фазы мнимая часть приравнивается к нулю и знак перед ней не играет роли, то операцию умножения на комплексную сопряженную функцию можно не проводить, приняв
. Однако поскольку при определении частоты переворота фазы мнимая часть приравнивается к нулю и знак перед ней не играет роли, то операцию умножения на комплексную сопряженную функцию можно не проводить, приняв ,
, .
. , тогда
, тогда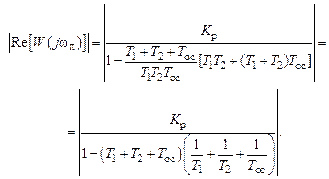
 , т.е.
, т.е. ,
, .
. ,
,  с,
с,  с,
с, 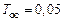 с. Тогда по полученным соотношениям при
с. Тогда по полученным соотношениям при  получим
получим  ,
,  , следовательно, система с такими параметрами будет неустойчивой. Ее граничный коэффициент передачи
, следовательно, система с такими параметрами будет неустойчивой. Ее граничный коэффициент передачи .
. (при единичном коэффициенте передачи) включено последовательно с системой без запаздывания с передаточной функцией
(при единичном коэффициенте передачи) включено последовательно с системой без запаздывания с передаточной функцией  .
. ,
,  .
. , то
, то .
. система станет неустойчивой.
система станет неустойчивой.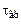 , что поясняется построением на рис. 4.11.
, что поясняется построением на рис. 4.11. пересекает окружность единичного радиуса на частоте
пересекает окружность единичного радиуса на частоте  (как будет показано ниже, это частота среза) при повороте радиус-вектора АФЧХ на угол
(как будет показано ниже, это частота среза) при повороте радиус-вектора АФЧХ на угол 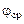 . При введении в САУ звена чистого запаздывания на границе устойчивости конец этого радиус-вектора совпадет с точкой
. При введении в САУ звена чистого запаздывания на границе устойчивости конец этого радиус-вектора совпадет с точкой  , отсюда
, отсюда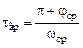 .
.



