
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ устойчивости нелинейных расСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
После линеаризации нелинейных элементов можно при заданных условиях оценить устойчивость РАС в целом [1, 4]. Для анализа устойчивости нелинейных РАС, выяснения возможности возникновения автоколебаний, определения их частоты и анализа устойчивости автоколебаний применяется метод гармонического баланса. Суть метода заключается в использовании модификации критерия Найквиста, который применяется к обратной (инверсной) АФЧХ – ОАФЧХ линейной части разомкнутой системы [1, 4]. Вернемся к формуле (8.25), которая связывает компоненты линейной и нелинейной частей разомкнутой РАС: ЧПФ разомкнутой системы зависит не только от частоты входного сигнала, но и от амплитуды. Критической точкой при использовании критерия устойчивости Найквиста является точка (–1, i 0). Если при изменении ω от 0 до ∞ годограф Найквиста проходит через эту критическую точку, то система будет нейтральна. В этом случае W (i ω, a) = –1, и в РАС могут возникнуть незатухающие колебания (автоколебания). Из формулы (8.25) следует:
Анализ на основе выражений (8.47) удобно проводить графически. Если годографы правой и левой частей не пересекаются, то автоколебания не возникают. При пересечении годографов (8.47) возможно существование автоколебаний в РАС. Значения частот в точках пересечения годографов определяют частоту автоколебаний. Устойчивость автоколебательного режима оценивается следующим образом [1, 4].
На рис. 8.19 приведен пример оценки устойчивости нелинейной РАС. График линейной части (сплошная линия на рис. 8.19) пересекает график 2 ОАФЧХ нелинейной части Пример 8.3. Для идеального релейного элемента (F(x) = c ×sign(x)), включенного в РАС, схема которой приведена на рис. 8.20, проанализируем возможность появления автоколебаний.
Проведем гармоническую линеаризацию нелинейного элемента:
хотя в данном случае легко построить график самой функции –1/F(x). Строим годографы для функций (рис. 8.21)
График 2 – при больших значениях параметра c, и в этом случае он практически совпадает с точным графиком –1/F(a). Точка a соответствует устойчивым автоколебаниям в обоих случаях, а в точке b нет пересечения графиков. И хотя при больших значениях c график нелинейной части приближается к точке b, автоколебаний все равно не возникнет, так как в этой точке w = 0.
Важным показателем качества работы нелинейной следящей РАС является вероятность срыва слежения. При выходе ошибки за пределы апертуры дискриминатора (например, под воздействием помех) исчезает напряжение на его выходе, что равносильно по действию размыканию петли регулирования. Через некоторое время ошибка слежения может вновь оказаться в пределах апертуры дискриминатора, и при определенных условиях нормальная работа РАС может возобновиться. Возникает проблема оценки работоспособности РАС в этих условиях.
Пример 8.4. Проанализируем условия работы РАС (рис. 8.22) с характеристикой дискриминатора F(x) = c ×sin(ax) при воздействии l(t) = l1 t и возмущении x(t) = N0. Пусть l1 = 3, N0 = 10, kл = 2, Tф = 1, с = 4, a = 0,1 [2]. Определим математическое ожидание ошибки слежения.
Определим дисперсию ошибки слежения.
Определим коэффициенты статистической линеаризации
Далее необходимо решить уравнения (8.48) и (8.49) совместно относительно переменных mx и s x. В [2, 18] это сделано графически, но проще это сделать с помощью «MathCad». При заданных условиях получаются такие значения: mx = 4,8; s x = 5,6; Dx = 31,4. Для дальнейшего анализа целесообразно построить графики таких зависимостей: Для исходных данных график 1 соответствует зависимости f1. Точка пересечения графиков 1 f1 и f2 определяет решение Dx = 31,4.
При большем уровне помех пересечений графиков не будет, решение системы (8.48) и (8.49) не существует – mx и s x неограниченно возрастают [2]. График 3 (f13), построенный при N0 = 30, соответствует именно этому случаю (срыв слежения). При увеличении математического ожидания график f2 сместится вверх, и критическое значение N0 уменьшится [2]. При статическом входном воздействии математическое ожидание в установившемся режиме будет равно нулю, а критическое значение N0 увеличится.
Список рекомендуемой литературы: [ 1, с. 238-246, 249-265; 2, с. 9-23, 129-156; 3, с. 473-489, 540-547; 4, с. 225-247; 5, с. 147-152, 163-166; 8; 10, т. 2, с. 4-11; 11, с. 477-507; 18, с. 129-137; 27, с. 32-35 ]. Контрольные вопросы 1. Какие принципиальные особенности имеют процессы в нелинейных РАС? 2. Какие виды нелинейностей характерны для типовых РАС? 3. Дайте характеристику явлений захвата и срыва сопровождения. 4. Опишите особенности нелинейной ЧАП. 5. Опишите особенности нелинейной ФАПЧ. 6. Дайте определение полосам захвата и синхронизма. 7. Как влияет на характеристики ФАПЧ применение корректирующего фильтра интегрирующего и пропорционально-интегрирующего типа? 8. Дайте характеристику методу кусочно-линейной аппроксимации. 9. Опишите метод статической линеаризации. 10. Объясните суть метода гармонического баланса. 11. Дайте характеристику методу фазовой плоскости. 12. Объясните понятие «срыв слежения». 13. Как определяют условия устойчивости нелинейных САУ? 14. Как влияет нелинейность дискриминатора на работу РАС? Дискретные и цифровые Радиоавтоматические системы Системы прерывистого регулирования. Дискретные системы; системы с конечным временем съема данных. Условия эквивалентности свойств дискретных и непрерывных систем управления. Методы математического описания дискретных систем с помощью разностных уравнений; с помощью дискретного преобразования Фурье, Лапласа и Z-преобразования; билинейного преобразования. Понятие типового дискретного звена и его математическое описание. Устойчивость дискретных РАС. Методы анализа детерминированных и случайных процессов в линейных дискретных системах. Показатели качества управления дискретных систем управления. Оценка ошибок слежения и быстродействия при детерминированных воздействиях. Оценка дисперсии ошибки слежения в установившемся режиме. Преимущества и недостатки цифровых систем управления по сравнению с аналоговыми. Математическое описание цифровых РАС. Методы анализа цифровых РАС: сведение к линейным дискретным системам, переход к эквивалентным непрерывным системам. Аналого-цифровые и полностью цифровые РАС. Погрешности цифровых систем управления.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.134 (0.009 с.) |

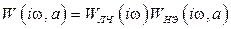 .
. или
или  . (8.47)
. (8.47) Режим автоколебаний устойчив, если при увеличении амплитуды (по сравнению с исходным значением) годограф нелинейной части перестает охватываться годографом линейной части. То есть для устойчивых автоколебаний в нелинейной РАС необходимо, чтобы с увеличением амплитуды входного сигнала амплитуда автоколебаний уменьшалась.
Режим автоколебаний устойчив, если при увеличении амплитуды (по сравнению с исходным значением) годограф нелинейной части перестает охватываться годографом линейной части. То есть для устойчивых автоколебаний в нелинейной РАС необходимо, чтобы с увеличением амплитуды входного сигнала амплитуда автоколебаний уменьшалась. в точках a и b, но не имеет точек пересечения с графиком 1. Таким образом, годограф нелинейной части 1 соответствует РАС, в которой автоколебания отсутствуют, а в РАС с годографом 2 могут существовать автоколебания. Точка a соответствует устойчивому режиму, а точка b – неустойчивому (увеличенная амплитуда). Значения амплитуды и частоты в точке a определяют соответственно характеристики автоколебаний.
в точках a и b, но не имеет точек пересечения с графиком 1. Таким образом, годограф нелинейной части 1 соответствует РАС, в которой автоколебания отсутствуют, а в РАС с годографом 2 могут существовать автоколебания. Точка a соответствует устойчивому режиму, а точка b – неустойчивому (увеличенная амплитуда). Значения амплитуды и частоты в точке a определяют соответственно характеристики автоколебаний.
 ,
,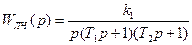 ;
;  .
. График 1 построен для линеаризованного звена с небольшими значениями параметра c.
График 1 построен для линеаризованного звена с небольшими значениями параметра c. Существует понятие «памяти системы». Например, астатическая система первого порядка обладает «памятью по положению». То есть при кратковременном размыкании системы за счет интегратора РАС будет некоторое время удерживать сигнал ошибки в пределах, позволяющих восстановить процесс слежения.
Существует понятие «памяти системы». Например, астатическая система первого порядка обладает «памятью по положению». То есть при кратковременном размыкании системы за счет интегратора РАС будет некоторое время удерживать сигнал ошибки в пределах, позволяющих восстановить процесс слежения. . (8.48)
. (8.48) . (8.49)
. (8.49) и
и 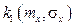 по формулам (8.42) – (8.44):
по формулам (8.42) – (8.44): ,
,  ,
, .
. и
и  (рис. 8.23).
(рис. 8.23). Срыв слежения в данном случае носит случайных характер. Если увеличить уровень шума (N0 = 18), то наклон прямой f1 уменьшится (график2, f12) до касания с графиком f2. Это критическое значение при данных условиях.
Срыв слежения в данном случае носит случайных характер. Если увеличить уровень шума (N0 = 18), то наклон прямой f1 уменьшится (график2, f12) до касания с графиком f2. Это критическое значение при данных условиях.


