
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование устойчивости стационарных состояний нелинейных систем второго порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Отдельно 21. Устойчивость и неустойчивость стационарного состояния (на примере гидродинамической модели). Примеры Модель Вольтерра В качестве второго примера рассмотрим классическую модель взаимодействия видов, которая впервые была предложена В. Вольтерра в тридцатые годы XX века для объяснения периодических изменений числа особей, так называемую вольтерровскую модель«хищник-жертва». Более подробно модели взаимодействия видов мы рассмотрим в Лекции 9. Пусть в некотором замкнутом районе живут хищники и жертвы, например, зайцы и волки. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Обозначим число зайцев (жертв) x, а число волков (хищников) – y. Так как количество пищи у зайцев неограниченно, мы можем предположить, что они размножаются со скоростью, пропорциональной их числу: Если рождаемость зайцев превышает их смертность, 0. Выражение (5.16) соответствует автокаталитической реакции первого порядка. Пусть убыль зайцев пропорциональна вероятности встречи зайца с волком, т.е. пропорциональна произведению численностей xy. Можно предположить по аналогии с бимолекулярными реакциями, где вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, что и количество волков нарастает тем быстрее, чем чаще происходят их встречи с зайцами, а именно, пропорционально xy. Кроме того, имеет место процесс естественной смертности волков, причем скорость смертности пропорциональна их количеству. Эти рассуждения приводят к системе уравнений для изменений численности зайцев-жертв x и волков-хищников y. Покажем, что система уравнений (5.17) имеет на фазовой плоскости переменных xy ненулевую особую точку типа центр. Координаты этой особой точки Так как все параметры
Рис. 5.3. Фазовый портрет системы 5.17. Особая точка типа «центр». а – параметры системы: x = 4, xy = 0,3, y = yx = 0,4 б – параметры системы: x =2, xy = 0,3, y = yx = 0,4 Здесь , - отклонения
Характеристическое уравнение системы (5.18): Корни этого уравнения чисто мнимые: Таким образом, исследование системы показывает, что траектории вблизи особой точки являются концентрическими эллипсами, а сама особая точка – центром. Расcматриваемая модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной, и определяется параметрами системы (рис. 5.3). Изменения численности жертвы и хищника во времени представляют собой колебания, причем колебания численности хищника отстают по фазе от колебаний жертв. Как мы уже отмечали в Лекции 4, особая точка типа центр устойчива по Ляпунову, но не асимптотически. Покажем на данном примере, в чем это проявляется. Пусть колебания x (t)и y (t) происходят таким образом, что изображающая точка движется по фазовой траектории 1 (рис 5.3). В момент, когда точка находится в положении М1, в систему добавляется извне некоторое число особей y такое, что изображающая точка переходит скачком из точки M1 в точку M2 . Если после этого систему предоставить самой себе, колебания x (t), y (t) уже будут происходить с большими амплитудами, чем прежде, и изображающая точка будет двигаться по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии.
Рис. 5.4. Кривые численности зайца и рыси в Канаде (по К. Вилли, В. Детье, 1974)
В дальнейшем мы рассмотрим модели, описывающие устойчивые колебательные режимы, и покажем, что на фазовой плоскости такие асимптотически устойчивые периодические движения описываются предельными циклами. На рис. 5.4 кривые колебаний численности пушных зверей по данным компании Гудзонова залива о числе заготовленных шкурок. Во всех классических учебниках в течение многих лет колебательный характер этих изменений приводили как подтверждение гипотез, положенных в основу модели Вольтерра, которую мы только что рассмотрели. Действительно, периоды колебаний численности зайцев (жертв) и рысей (хищников) примерно одинаковы и составляют порядка 9 – 10 лет. При этом максимум численности зайцев опережает, как правило, максимум численности рысей на один год. Можно полагать, что мы видим регулярные колебания, осложненные случайными факторами, связанными с погодой и проч. Однако возможна и другая интерпретация этих данных наблюдений на основе моделей детерминированного хаоса. О дискретных моделях такого типа мы уже говорили в Лекции 3. Непрерывные модели популяционной динамики, приводящие к детерминированному хаосу, мы рассмотрим в Лекции 9. Серьезным недостатком рассмотренной модели Вольтерра является неустойчивость решений по отношению к малым случайным воздействиям, приводящим к изменению переменных. Кроме того, в силу «негрубости» этой системы произвольно малое изменение вида правых частей уравнений (величин параметров системы) приведет к изменению типа особой точки, и, следовательно, к изменению характера фазовых траекторий. Поскольку природные системы подвергаются огромному количеству случайных воздействий, реалистическая модель должна быть по отношению к ним устойчивой. Поэтому негрубые системы не могут давать адекватное описание природных явлений. Различные модификации рассмотренной нами системы, изученные самим Вольтерра и другими авторами, лишены этих недостатков. Наиболее широко известные из них будут рассмотрены в Лекции 9. Здесь мы остановимся на модели, которая учитывает самоограничение в росте обеих популяций. На ее примере видно, как может меняться характер решений при изменении параметров системы. Итак, рассмотрим систему: Система (5.19) отличается от ранее рассмотренной системы наличием в правых частях членов: Эти члены отражают тот факт, что численность популяции жертв не может расти до бесконечности даже в отсутствие хищников в силу ограниченности пищевых ресурсов, ареала существования и проч. Такие же «самоограничения» накладываются на популяцию хищников. Система имеет два стационарных решения: нулевое и ненулевое. Анализ показывает, что нулевое решение представляет собой неустойчивый узел. Рассмотрим систему алгебраических уравнений, решение которых дает координаты ненулевого стационарного состояния. Стационарное решение: Корни характеристического уравнения системы, линеаризованной в окрестности особой точки: Из выражения для характеристических чисел видно, что если выполнено условие то численности хищников и жертв совершают во времени затухающие колебания. Система имеет особую точку – устойчивый фокус.
Рис. 5.5. Фазовый портрет системы 5.19 а – устойчивый фокус, параметры системы: x = 2, xy = 18, x =1, y = 3, yx = 5, y =1 б – устойчивый узел, параметры системы: x = 2, xy = 1, x =1, y = 3, yx = 1, y =1
При изменении знака неравенства на обратный точка становится устойчивым узлом. И в том и в другом случае стационарное состояние асимптотически устойчиво, и решение устойчиво к малым изменениям правых частей уравнений. Таким образом, самоограничение популяции приводит к устойчивости ее численности. Важно отметить,чтопростейшие вольтерровские модели, которые мы рассмотрели, не могут описывать устойчивые колебания с постоянными периодом и амплитудой. Для описания таких колебаний необходимы нелинейные модели, имеющие на фазовой плоскости предельный цикл. Они будут рассмотрены в Лекции 8.
Теорема 1 Если существует дифференцируемая функция V (x1,…,xn), удовлетворяющая в окрестности начала координат следующим условиям: a) V(x1,…,xn) 0, причем V(x1,…,xn) = 0 лишь в начале координат; б) причем то точка покоя системы (5.21) устойчива. Теорема 2 Если существует дифференцируемая функция V (x1,…,xn), удовлетворяющая в окрестности начала координат следующим условиям: a) V(x1,…,xn) = 0 и сколь угодно близко от начала координат имеются точки, в которых V(x1,…,xn) > 0; б) причем то точка покоя системы (5.21) неустойчива. С доказательством этих теорем можно познакомиться в книге Л.Э. Эльсгольц «Теория дифференциальных уравнений» или в других учебниках по теории дифференциальных уравнений. Общего методы построения функции Ляпунова не существует. Однако для линейных автономных систем ее следует искать в виде: и т.п., подбирая надлежащим образом коэффициенты a > 0, b > 0. Для нелинейных систем a и b могут быть произвольных знаков.
Примеры 1. Рассмотрим линейную систему: Выберем функцию Ляпунова: V = x 2 +y 2. Тогда Это выражение всегда отрицательно при х 0, т.к. в скобках стоят четные степени x. Следовательно, точка (0, 0) устойчива.
2. Рассмотрим систему уравнений, описывающую конкуренцию видов, численности которых x и y. Каждый из видов размножается в соответствии с логистическим законом, а при встрече (произведения в правых частях уравнений), численность как одного, так и другого вида уменьшается. Исследуем стационарное состояние, соответствующее сосуществованию видов (x, y) – ненулевое для x и y. Его координаты: В. Вольтерра показал, что стационарное состояние (5.23) устойчиво для параметров системы a > 0, b 1, построив функцию Ляпунова: Ее производная равна и отрицательна при малых значениях коэффициентов a, b и x, y > 0. Доказательство приведено в книге В. Вольтерра. «Математическая теория борьбы за существование» (М., 1976)
Вдали от равновесия поведением системы управляют нелинейность и внешние ограничения, в чем мы убедились, рассматривая примеры самоорганизации, например условия появления ячеек Бенара. Теперь выделим наиболее общие черты переходов, происходящих в различных системах при удалении от состояния равновесия. Пусть Х – переменное состояние системы (например, вертикальная составляющая скорости закручивания жидкости в ячейке Бенара), которая изменяется под действием управляющего (возмущающего систему) параметра λ (например, разности температур Термин Бифуркация означает «развилка» или «разделение надвое» (от лат. Bi – двойной, Furca – развилка). При И. Пригожин и Г. Николис писали: «Довольно заманчиво на мгновение вообразить, что вместо шарика мог оказаться динозавр конца мезозойской эры или группа наших предков, собирающаяся принять идеографическую или символическую письменность». Бифуркация – неотъемлемый этап процесса развития. Ее нельзя предотвратить и избежать. Социальные, экономические, политические системы, в которых мы живем, сложны и нестабильны. Рано или поздно их эволюционные пути должны претерпеть бифуркацию. За последнее полстолетия мы стали свидетелями двух гигантских такого рода бифуркаций: первая – волна деколонизации, вторая – волна гласности.
22. Активный транспорт (электрогенный транспорт ионов – опыт Уссинга и). Активный транспорт 1. Na+ - K+-насос осуществляется за счет противоградиентного переноса через мембрану трех ионов натрия из клетки и накачивающий два иона калия внутрь клетки. 1. Основные этапы Na+ - K+-насоса: образование комплекса фермента с АТФ на внутренней поверхности мембраны (эта реакция активируется ионами магния) 2. связывание комплексом трех ионов натрия 3. фосфолирирование фермента с образованием аденозинтрифосфата 4. переворот фермента внутри мембраны 5. реакция ионного обмена натрия на калий, происходящая на внешней поверхности мембраны 6. обратный переворот ферментного комплекса с переносом ионов калия внутрь клетки 7. возращение фермента в исходное состояние с освобождением ионов калия и неорганического фосфата
2. Активный транспорт ионов кальция осуществляется через мембрану саркоплазмотического ретикулума. Ca2+ - насос идет за счет энергии гидролиза АТФ и переноса двух ионов кальция из клетки в межклеточное пространство. • Первый этап: связывание Са2+ с комплексом Mg-АТФазы на наружной поверхности саркоплазматической мембраны. • Второй этап: гидролиз АТФ с образованием фермент-фосфатного комплекса. • Третий этап: переход связанного Са2+ через мембрану в клетку. • Четвертый этап: переход кальцийсвязывающих центров на наружную поверхность мембраны
Перенос веществ через сложные мембраны можно рассмотреть на примере опыта Уссинга. Камера, заполненная нормальным раствором Рингера, разделена на две части свежеизолированной кожей лягушки. Слева - наружная поверхность кожи, справа - внутренняя серозная. Поток ионов Na+ через кожу идет от наружной к внутренней поверхности и наоборот. На коже лягушки возникает разность потенциалов: внешняя сторона имеет отрицательный заряд, внутренняя сторона имеет положительный заряд. Уравнение Уссинга Направление и скорость диффузии зависит от концентрации градиентов. Где Мск - поток вещества из среды в клетку Мкс - поток вещества из клетки в среду
вещества в клетке Сс – концентрация вещества в среде 23. Понятие обобщенных сил и потоков. Соотношение взаимности Онзагера. Теорема Пригожина. Обобщенные потоки и термодинамические силы могут быть связаны так называемыми соотношениями Онзагера. Эта связь ограничивается принципом Кюри, запрещающим взаимную связь явлений различной тензорной размерности. Допустим, что все обобщенные потоки и обобщенные силы, входящие в выражения для производства энтропии или для диссипативной функции, обращаются в нуль при достижении системой состояния с нулевым производством энтропии. Этому условию отвечает либо подлинно внутреннее равновесное состояние системы, либо такое ее стационарное состояние при наличии внешнего поля, когда перенос всех обобщенных координат прекращается, хотя система и остается неоднородной. Поэтому на более высокий уровень иерархии по системе связи передается некоторый обобщенный поток информации. Исполнительными системами объекта, к которым направляется поток управляющих воздействий, могут быть различные виды автоматических устройств и систем, роботы, а также технический персонал объекта. В состоянии полного равновесия системы (напомним, что система находится в полном равновесии, если она термодинамически равновесна и неподвижна) все обобщенные потоки и все обобщенные силы равняются нулю. В термодинамике необратимых процессов Ларс Онзагер сформулировал следующее положение: при небольших отклонениях от равновесия термодинамический поток можно представить в виде линейной комбинации термодинамических движущих сил:
Здесь
Соотношения типа (4.1) для систем, близких к равновесию, называют соотношениями взаимности Онзагера или линейными соотношениями. С учётом (4.1) производство энтропии системы можно представить в виде квадратичной формы:
Данная квадратичная форма является положительно определённой (доказательство приводится в разделе "Характеристика производства энтропии"). Л. Онзагер также определил, что в линейных соотношениях (4.1) недиагональные коэффициенты равны [9]:
т.е. матрица феноменологических коэффициентов должна быть симметричной. Иными словами, если на поток Теорема Пригожина — теорема термодинамики неравновесных процессов. Согласно этой теореме, стационарному состоянию системы (в условиях, препятствующих достижению равновесного состояния) соответствует минимальное производство энтропии. Если таких препятствий нет, то производство энтропии достигает своего абсолютного минимума — нуля. Доказана И. Р. Пригожиным в 1947 из соотношений взаимности Онсагера. Теорема Пригожина справедлива, если кинетические коэффициенты в соотношениях Онсагера постоянны; для реальных систем она справедлива лишь приближённо, поэтому минимальность производства энтропии для стационарного состояния не является столь общим принципом, как максимальность энтропии для равновесного состояния. Формулировка теоремы: В стационарном состоянии продукция энтропии внутри термодинамической системы при неизменных внешних параметрах является минимальной и константной. Если система не находится в стационарном состоянии, то она будет изменяться до тех пор, пока скорость продукции энтропии, или, иначе, диссипативная функция системы не примет наименьшего значения. 24. Простая и облегченная диффузия. Облегченная диффузия При облегченной диффузии вещества пересекают мембрану путем взаимодействия с транспортными белками. Крупные полярные молекулы транспортируются белками-переносчиками, а заряженные ионы — белками трансмембранных каналов. • Диффузия происходит по электрохимическому градиенту. • Вещества связываются с белком-переносчиком, который в процессе переноса вещества через мембрану испытывает обратимые конформационные изменения*. • Диффузия — ограниченный по скорости и насыщаемый процесс, поскольку зависит от наличия в мембране определенного количества белков-переносчиков или белков каналов*. • Энергия на диффузию не расходуется. 25. Кооперативные свойства макромолекул (механизм кооперативного связывания кислорода гемоглобином и миоглобином). Кооперативные взаимодействия – специфические взаимодействия комплементарных макромолекул за счет образования достаточно протяженной последовательности физических связей между ними. Такая система физических связей устойчива даже в тех случаях, когда энергия диссоциации отдельной связи чрезвычайно мала. Это обусловлено тем, что при разрыве единичной связи «проигрыш» в свободной энергии не компенсируется возрастанием энтропии. Результаты исследований кооперативных взаимодействий между комплементарными макромолекулами привели к получению принципиально нового класса полимерных материалов – полимер-полимерных комплексов (поликомплексов), свойства которых коренным образом отличаются от свойств исходных полимеров. Например, при смешении растворов двух полимеров образуется нерастворимый поликомплекс, выпадающий в осадок. Отметим, что в живой природе примером кооперативного поликомплекса служит двойная спираль ДНК. Устойчивые поликомплексы возникают только в том случае, если степени полимеризации (количество мономерных звеньев, а, значит, и взаимодействующих групп) в макромолекулах реагентов превышают определенные критические значения. Эти критические значения зависят от природы взаимодействующих полимеров и, в общем случае, лежат в пределах от нескольких мономерных звеньев до нескольких сотен. Поликомплексы образуются и разрушаются в узких интервалах изменения внешних условий: температуры, качества растворителя, рН, ионной силы раствора и т.д., что свидетельствует об их кооперативной природе. Очевидно, что образование поликомплекса возможно лишь при одновременном (кооперативном) взаимодействии функциональных групп комплементарных макромолекул в количестве, превышающем критическое. И наоборот, разрушение поликомплекса требует одновременной (кооперативной) диссоциации системы связей между образующими его макромолекулами. Поликомплексы получают либо смешением растворов полимеров, либо матричным синтезом. Известны поликомплексы между макромолекулами изо- и синдиотактического полиметилметакрилата (стереокомплексы), стабилизированные силами Ван-дер-Ваальса, поликомплексы,
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 985; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.019 с.) |

 (5.16)
(5.16) (5.17)
(5.17)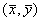 легко найти, приравняв правые части уравнений системы (5.17) нулю. Это дает стационарные ненулевые значения:
легко найти, приравняв правые части уравнений системы (5.17) нулю. Это дает стационарные ненулевые значения: .
. положительны, точка
положительны, точка  (5.18)
(5.18)

 численностей от их стационарных значений:
численностей от их стационарных значений:

 .
.
 (5.19)
(5.19)
 (5.20)
(5.20)

 .
.



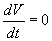 лишь при x 1 = … =xn = 0,
лишь при x 1 = … =xn = 0,



 (5.22)
(5.22) . (5.23)
. (5.23) .
.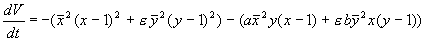
 в бенаровской задаче). Вид зависимости Х (λ) получил название бифуркационной диаграммы.
в бенаровской задаче). Вид зависимости Х (λ) получил название бифуркационной диаграммы. система характеризуется устойчивостью, и это состояние изображено термодинамической ветвью А. В бенаровском эксперименте А – стационарное состояние покоя жидкости. В этой области система гасит все внутренние флуктуации или внешние воздействия. В точке
система характеризуется устойчивостью, и это состояние изображено термодинамической ветвью А. В бенаровском эксперименте А – стационарное состояние покоя жидкости. В этой области система гасит все внутренние флуктуации или внешние воздействия. В точке  , в которой сливаются два режима, называется Точкой бифуркации. В ней, находясь в состоянии неустойчивости, система совершает критический выбор – либо ветвь В1, либо ветвь В2, т. е. или R или L в данной ячейке Бенара. Причем заранее решение предсказать невозможно, решает лишь случай через динамику флуктуаций. Просканировав «фон», система совершит несколько попыток и, наконец, какая-то флуктуация победит. Стабилизировав ее, система сделает выбор дальнейшего развития, став таким образом историческим объектом. Следовательно, можно утверждать, что переход к сложному связан с появлением новых ветвей решения в результате испытания системной бифуркации.
, в которой сливаются два режима, называется Точкой бифуркации. В ней, находясь в состоянии неустойчивости, система совершает критический выбор – либо ветвь В1, либо ветвь В2, т. е. или R или L в данной ячейке Бенара. Причем заранее решение предсказать невозможно, решает лишь случай через динамику флуктуаций. Просканировав «фон», система совершит несколько попыток и, наконец, какая-то флуктуация победит. Стабилизировав ее, система сделает выбор дальнейшего развития, став таким образом историческим объектом. Следовательно, можно утверждать, что переход к сложному связан с появлением новых ветвей решения в результате испытания системной бифуркации. Ск – концентрация
Ск – концентрация
 - движущая сила, сопряжённая с потоком
- движущая сила, сопряжённая с потоком  ; она определяет прямой эффект.
; она определяет прямой эффект.  - движущие силы, сопряжённые с другими потоками; они характеризуют в (4.1) перекрёстные эффекты по отношению к процессу i. Коэффициенты L называют феноменологическими коэффициентами:
- движущие силы, сопряжённые с другими потоками; они характеризуют в (4.1) перекрёстные эффекты по отношению к процессу i. Коэффициенты L называют феноменологическими коэффициентами:  - при прямом эффекте,
- при прямом эффекте,  - при перекрёстных эффектах, причём влияние прямого эффекта существенно превышает влияние перекрёстных эффектов:
- при перекрёстных эффектах, причём влияние прямого эффекта существенно превышает влияние перекрёстных эффектов:


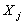 необратимого процесса j, то сила
необратимого процесса j, то сила  с тем же коэффициентом
с тем же коэффициентом  . Соотношения (4.2) называют принципом симметрии феноменологических коэффициентов.
. Соотношения (4.2) называют принципом симметрии феноменологических коэффициентов.


