
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие эквивалентной шумовой полосы пропускания системыСодержание книги
Поиск на нашем сайте
Определение дисперсии и СКО рассмотренным выше методом при больших порядках интеграла (6.14) оказывается затруднительным. Поэтому стали использовать графоаналитический метод [10], в основу которого положен геометрический смысл интеграла: значение интеграла равно площади, которая находится под графиком подынтегральной функции. Для вычисления дисперсии по формуле (6.13) или (6.11)–(6.13) строят график подынтегральной функции С учетом четности подынтегральной функции достаточно построить график только для положительных частот (формула (6.9)).
В настоящее время вычисления проще всего проводятся с помощью численного интегрирования в специальных математических программах. Пример 6.3. Найдем дисперсию для РАС и возмущения, рассмотренных в примере 6.1 (k 0 = 200, Sд = 10). После подстановки ЧПФ (6.17) и S (ω) формула (6.18) имеет вид:
С помощью численного интегрирования в MathCad, можно вычислить площадь и дисперсию (6.20) напрямую: Sэкв = 3,32×10–3, тогда Dx = = 3,32×10–3/p = 1,06×10–3, что совпадает с полученным ранее значением. Пример 6.4. Найдем дисперсию для РАС и возмущения, рассмотренных в примере 6.2. После подстановки численных значений в ЧПФ (формула (6.21)) и S (ω), а затем в формулу (6.18) строим график подынтегральной функции (рис. 6.2) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 трапецию и 1 треугольник. После вычислений получаем Sэкв ≈ 1,3×10–3, Dx ≈ 1,3/p ≈ 4,1×10–4. При численном интегрировании в MathCad дисперсия Dx = 4,2×10–4.
Если на РАС действует широкополосная помеха с равномерным спектром, ее можно считать белым шумом. В этом случае вводят понятие эквивалентной шумовой полосы ω экв (эффективной шумовой полосы ω эф), под которой понимается величина, равная полосе пропускания эквивалентной РАС с прямоугольной АЧХ, с одинаковой с исходной системой ЧПФ на нулевой частоте (рис. 6.2) и одинаковой дисперсией выходного процесса при действии на входах этих систем белого шума. Из приведенного определения и выражения (6.13) вытекает (будем рассматривать только положительные частоты f или ω) формула:
Зная эквивалентную шумовую полосу РАС, сведенную к обобщенному виду, можно легко определить дисперсию
В данном случае в обобщенной РАС действие белого шума приведено ко входу дискриминатора, крутизна которого Sд. Для графика на рис. 6.1 эквивалентная шумовая полоса ω эф образует прямоугольник по уровню ≈1×10–5 и до частоты ω экв ≈ 330 рад/с. Для графика на рис. 6.2 эквивалентная шумовая полоса ωэф образует прямоугольник по уровню ≈9×10–6 и до частоты ω экв ≈ 159 рад/с. Если S (ω) случайного процесса отличается от константы, этот процесс можно свести к белому шуму, добавив в схему устройство, называемое формирующим фильтром [1, 4], на выходе которого процесс будет иметь такую же S (ω). В табл. 6.1 приведены некоторые формулы для определения fэф по ПФ разомкнутой системы W(p). Табл. 6.1
Пример 6.5. Найдем дисперсию при возмущении ξ(t) = N0 для РАС, схема которой показана на рис. 5.1, при ПФ звеньев K1 = Sд – безынерционный дискриминатор, K2 = k 0(1 + pT2)/(p + p2T1) – интегратор вместе с пропорционально-интегрирующим фильтром (ПИФ). Для ПФ ошибки по возмущению из (2.30) после подстановки имеем:
После замены переменных р ® i ω и подстановки в (6.14) получим:
Подставляя эти значения в (6.16) найдем дисперсию:
где a = Т2 / Т1 – отношение постоянных времени ПИФ. С помощью понятия эквивалентной шумовой полосы можно было определить дисперсию по-другому. Для этого необходимо перенести пересчитать воздействие ко входу дискриминатора (ξ д (t) = N0 / Sд2) и воспользоваться формулой (6.26) и таблицей 6.1 при W (p) = K1K2 = k 0 Sд (1 + pT2)/(p + p2T1):
Рассмотрим некоторые соотношения параметров РАС и проанализируем их влияние на характеристики системы. При Т2 = 0, получается то же соотношение для fэф, что и для фильтра системы, состоящему из одного интегратора (для Dx значение Т1 не имеет значения!):
Из формулы (6.32) видно, что РАС с одним интегратором в контуре управления по фильтрации шумов эквивалентна инерционному звену с постоянной времени Т1 = 1/ k 0 Sд, на вход которого подан шум с S (ω) = N0 / Sд2. Если на входе такого фильтра действует шум с S (ω) = N0, то В случае применения в системе ПИФ существует оптимальное значение параметров Т2 и a, при которых дисперсия ошибки минимальна. Пример 6.6. Определим дисперсию ошибки слежения в установившемся режиме в РАС из примера 6.5 при Т2 = Т1 = 0, т. е.
С учетом (6.33) Для приведения интеграла к виду (6.14) преобразуем следующим образом:
Из сравнения (6.34) с (6.14) вытекает, что в данной задаче n = 2; b1 = –2μ D W, b0 = 0; a2 = 1, a1 = μ + k 0 Sд, a0 = μk 0 Sд. Подставляя эти значения в (6.16) получаем:
В данном случае вычисление дисперсии через fэф затруднительно из-за сложных преобразований S (ω) и отсутствия соответствующей W (p) в табл. 6.1. Таким образом, дисперсия ошибки данной РАС зависит от дисперсии воздействия D W, ширины спектра этого воздействия, характеризующейся параметром μ = 1/ Т, и коэффициента передачи по контуру управления k 0 Sд.
Список рекомендуемой литературы: [ 1, с. 93-95; 2, с. 91-128; 3, с. 202-213, 232-238, 293-337; 4, с. 95-113; 5, с. 104-124; 6, с. 45-51; 10, т. 2, с.142-144, 180-198, 218-225; 11, с. 386-427, 434-441, 452-458, 471-476; 18, с. 76-91; 27, с. 37-55]. Контрольные вопросы 1. Какие виды случайных процессов характерны для РАС? 2. Назовите основные характеристики случайных процессов. 3. Как определяют ошибку слежения и дисперсию РАС при случайных воздействиях? 4. Что такое «эквивалентная шумовая полоса РАС»? 5. Дайте определение среднеквадратической ошибке САУ. 6. Как вычисляется среднеквадратическая ошибка РАС? 7. Дайте определение корреляционной функции. 8. Опишите особенности нормального закона распределения. 9. В каком случае графоаналитический метод удобнее аналитического? 10. Как определяется дисперсия через корреляционную функцию?
Синтез линейных рас Задачи синтеза САУ. Методы синтеза линейных САР. Частотный метод. Инженерный метод синтеза минимально-фазовых систем с помощью ЛАЧХ. Понятия «неизменяемой» и «желаемой» ЛАЧХ. Корректирующие устройства: разновидности, способы включения, эффективность коррекции, взаимозаменяемость. Синтез последовательного корректирующего звена. Постановка задачи оптимального синтеза. Критерии оптимизации. Синтез фильтров РАС методами теории оптимальной линейной фильтрации. Фильтры Винера и Калмана. Условия физической реализуемости фильтров. Интегральное уравнение для ПХ и ИХ оптимального линейного фильтра. Определение ЧПФ оптимального линейного фильтра. Минимизация эффективного значения ошибки методом оптимизации параметров исходных динамических звеньев. Определение потенциальной точности слежения системы управления, использующей оптимальный фильтр. Примеры синтеза оптимального фильтра для РАС.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.255.103 (0.008 с.) |

 +
+  (в докомпьютерные времена эти построения выполняли по точкам, взятым на различных частотах ω j [10]) и вычисляют площадь под ним (в докомпьютерные времена эти вычисления осуществляли с помощью аппроксимации графика и площади под ним прямоугольниками и трапециями [10]).
(в докомпьютерные времена эти построения выполняли по точкам, взятым на различных частотах ω j [10]) и вычисляют площадь под ним (в докомпьютерные времена эти вычисления осуществляли с помощью аппроксимации графика и площади под ним прямоугольниками и трапециями [10]).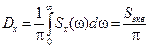 . (6.24)
. (6.24) . (6.25)
. (6.25) После подстановки численных значений строим график подынтегральной функции (рис. 6.1) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 прямоугольник и 3 треугольника, как показано на рис. 6.1). После вычисления площадей получаем Sэкв ≈ 3,4×10–3, подставляя в (6.24) вычисляем Dx ≈ 3,4×10–3/p ≈ 1,08×10–3.
После подстановки численных значений строим график подынтегральной функции (рис. 6.1) и вычисляем площадь (это удобно сделать с помощью разбиения на 1 прямоугольник и 3 треугольника, как показано на рис. 6.1). После вычисления площадей получаем Sэкв ≈ 3,4×10–3, подставляя в (6.24) вычисляем Dx ≈ 3,4×10–3/p ≈ 1,08×10–3.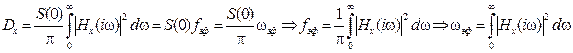 . (6.26)
. (6.26)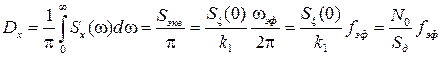 . (6.27)
. (6.27) . (6.28)
. (6.28) ,
,  . (6.29)
. (6.29) , (6.30)
, (6.30) . (6.31)
. (6.31) . (6.32)
. (6.32) .
. . Считаем, что ξ(t) = 0, а воздействие λ(t) является стационарным случайным процессом со спектральной плотностью
. Считаем, что ξ(t) = 0, а воздействие λ(t) является стационарным случайным процессом со спектральной плотностью  и дисперсией D W. Такой процесс характерен для входного сигнала РАС при слежении радиолокационной системы за движущимся с угловой скоростью W объектом. m = 1/ Т – среднее число перемен скорости за период времени, равный одной секунде (или Т = 1/m – среднее значение интервала времени, в течение которого W сохраняет постоянное значение) [1–5].
и дисперсией D W. Такой процесс характерен для входного сигнала РАС при слежении радиолокационной системы за движущимся с угловой скоростью W объектом. m = 1/ Т – среднее число перемен скорости за период времени, равный одной секунде (или Т = 1/m – среднее значение интервала времени, в течение которого W сохраняет постоянное значение) [1–5]. . (6.33)
. (6.33) . (6.34)
. (6.34) . (6.35)
. (6.35)


