
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В РАС в качестве корректирующих звеньев используются пассивные и активные электрические цепи.Содержание книги
Поиск на нашем сайте
Корректирующие устройства подразделяются на · линейные и нелинейные, · пассивные и активные, · с коррекцией по постоянному и переменному напряжениям. По виду включения в РАС корректирующие устройства подразделяются на · последовательные, · параллельные, · с местной обратной связью, · с комбинированным управлением.
Последовательное включение корректирующего звена КК (рис. 7.2).
Обычно так включают корректирующие звенья интегрирующего типа. Введение интегрирующего звена в данном случае повышает точность системы за счет увеличения порядка астатизма системы.
Параллельное включение корректирующего звена (рис. 7.3). Обычно при таком включении используют дифференцирующие звенья. Как известно, такие звенья вызывают подъем высоких частот. Применение подобных звеньев позволяет повысить запас устойчивости в области ОВЧ. Включение корректирующего звена с местной обратной связью показано на рис. 7.4, а на рис. 7.5 – включение звена с комбинированным управлением.
Различают такие виды местной обратной связи: · жесткая обратная связь: КК = kос; · инерционная жесткая обратная связь: · гибкая обратная связь: КК = kосp; · инерционная гибкая обратная связь: Рассмотрим влияние жесткой обратной связи (КК = kос) на инерционное (W(p) = k0 /(1 + pT0)) и интегрирующее (W(p) = k0 / p) звенья [4]. K(p) = k0 /(1 + k0kос + pT0), kэкв = k0 /(1 + k0kос), Tэкв = T0 /(1 + k0kос). (7.6) Таким образом, охват инерционного звена жесткой обратной связью не изменяет его характера (K(p) = kэкв /(1 + pTэкв)), но при этом коэффициент усиления и постоянная времени звена уменьшаются в (1 + k0kос) раз. При охвате интегрирующего звена жесткой обратной связью изменяется тип звена: получается инерционное звено с ПФ K(p) = kэк в/(1 + pTэкв). K(p) = k0 /(k0kос + p) = Гибкая обратная связь содержит дифференцирующие звенья и действует только в переходном режиме. В результате точность РАС в установившемся режиме не изменяется [4]. Рассмотрим влияние гибкой инерционной обратной связи ( Для безынерционного звена получаем:
что эквивалентно включению в РАС последовательного звена с отставанием по фазе. Для интегрирующего звена (W(p) = k0 / p) получаем:
где kэкв = k0 /(1 + k0Тос), Тэкв = Тос /(1 + k0Тос), что эквивалентно включению в РАС последовательного звена с опережением по фазе [4]. Звенья с комбинированным управлением (рис. 7.5) могут придать РАС особые свойства. Например, при Пример наклон ЛАЧХ на участке до w с1 = –20 дБ/дек, на участке w с1 – w с2 = –40 дБ/дек, w с2 – w с3 = –20 дБ/дек, и после w с3 = = –40 дБ/дек). Построенная по исходным данным асимптотическая ЛАЧХ изображена на рис. 7.6. Необходимо разбить ЛАЧХ на элементарные участки, которым можно будет поставить в соответствие типовые динамические звенья первого и второго порядков (прил. 2). Возможны несколько вариантов разбиения системы на элементарные звенья. На рис. 7.7 приведены ЛАЧХ трех динамических звеньев, каскадное соединение которых дает заданную ЛАЧХ: два звена интегрирующих с запаздыванием (1 с w с1 и 3 с w с3), и одно изодромное (2 с wс2).
ПФ каскадного соединения звеньев:
С учетом соотношения между постоянной времени и частотой сопряжения звена (Ti = 1/wсi) получаем: T1 = 0,1 с, T2 = 0,01 с, T3 = 0,33 мс.
На основании ПФ (7.10) и данных рис. 7.7 получаем электрическую схему, изображенную на рис. 7.9. Определим номиналы элементов. Пусть k1 = k2 = k3 =10 (20 дБ). R2C1 = T1 = 0,1 с, пусть C1 = 1 мкФ, тогда R2 = 100 кОм, а R1 = 10 кОм. R4C2 = T3 = 0,33 мс, пусть C2 = 33 нФ, тогда R4 = 100 кОм, а R3 = 10 кОм.
R6C3 = T2 = 0,01 с, пусть C3 = 10 мкФ, тогда R6 = 1 кОм, R7 = 100 кОм, а R5 = 10 кОм. Сопротивление R7 в изодромное звено введено для получения необходимого КУ по постоянному напряжению.
При применении инверсии фазы в одном или трех каскадах график ЛФЧХ сместится на 180° вниз, и соответственно изменятся запасы устойчивости. При практической реализации схемы, показанной на рис. 7.9, следует выбирать включение и цепи коррекции операционных усилителей так, чтобы каждый каскад оставался устойчивым. На рис. 7.10 сплошной линией приведена ЛАЧХ синтезированной схемы.
На рис. 7.10 также приведена ЛФЧХ системы и определены запасы устойчивости по усилению (LЗ = 130 дБ) и по фазе (jЗ = 55°). На рис. 7.11 изображены графики ПХ и ИХ.
Оптимизация РАС При проектировании РАС по заданным показателям качества, характеристикам сигналов и помех требуется обеспечить наилучшие характеристики работы или характеристики не хуже заданных. Спроектированная в результате РАС называется оптимальной. Так как различные параметры системы могут по-разному влиять на выходные характеристики, обычно требуется находить компромиссное решение, руководствуясь выбранным критерием оптимальности. Несложно спроектировать РАС, которая позволяла бы получать сколь угодно малую ошибку обработки управляющего воздействия, либо малую ошибку от воздействия помех, однако одновременно удовлетворить требование минимальной ошибки по управляющему воздействию и по возмущению (помехам) оказывается невозможным. Анализ показывает, что обобщенная РАС обрабатывает входное воздействие подобно ФНЧ Наиболее распространенным критерием оптимизации является критерий минимума среднеквадратичной ошибки (СКО). При заданной структурной схеме оптимизация РАС связана лишь с изменением параметров элементов схемы. Обычно такими параметрами оптимизации являются коэффициенты передачи по постоянному напряжению ( Аналитически задача решается взятием производной от функции СКО по параметру оптимизации; определив нули производной, находят оптимальное значения параметра. Пример 7.3. Рассмотрим пример оптимизации обобщенной РАС (рис. 3.2) при K1 = Sд и Математическое ожидание установившегося значения ошибки равно: Дисперсия ошибки слежения в установившемся режиме равна:
С помощью формулы (П.2) прил. 3 получаем:
Формула для СКО запишется так:
Для определения экстремумов (7.14) продифференцируем функцию СКО по параметрам T и k2 и приравняем производные к нулю:
Решая уравнения (7.15) и (7.16) совместно относительно параметров T и k2 получаем оптимальные значения:
Существование оптимального значения k2 объясняется тем, что при малых значениях k2 увеличивается составляющая динамической ошибки (по воздействию λ(t)), а при больших k2 возрастает дисперсия флуктуационной ошибки, обусловленной действием шума. Качество переходного периода при найденном значении Топт получается удовлетворительным, а его длительность Тр» 3 Топт . Если время регулирования потребуется уменьшить, то при уменьшении Т менее Топт, будет возрастать СКО из-за увеличения Dx, для компенсации этого потребуется коррекция параметров элементов схемы (Sд, k2). Пример 7.4. Рассмотрим, как с помощью «MathCad» можно провести оптимизацию РАС из примера 6.1 (при Sд = 0,4) по параметру Т2 с целью получения минимума СКО и Тр.
Штриховой линией показано исходное значение Т2 = 4,7 мс. Из графика видно, что минимальное значение дисперсии Dx достигается при Т2 = 20 – 25 мс. При этом очевидно, что вкладом математического ожидания mx в СКО можно пренебречь. С помощью функций и команд «MathCad» уточняем: минимум Dx (Dx = 0,27) достигается при Т2 = 22 мс, при Т2 = 20 мс и при Т2 = 25 мс Dx = 0,272, а при Т2 = 30 мс Dx = 0,28. Проанализируем теперь, как влияет изменение варьируемого параметра Т2 на время регулирования Тр. Анализ показывает, что приемлемая форма ПХ получается при Т2 > 21 мс.
На рис. 7.13 приведены графики ПХ и ИХ, построенные при следующих значениях варьируемого параметра: график 1 построен при начальном значении Т2 = 4,7 мс, график 2 – при критическом значении Т2 = 21 мс, а график 3 – при значении Т2 = 30 мс. Очевидно, что форма ПХ при Т2 = 4,7 мс (график 1) неудовлетворительна. Для существенного снижения Тр необходимо, чтобы на критическом участке ПХ не выходила из интервала установления (0,95 < h (t) <1,05). Это достигается при Т2 > 21 мс. ПХ на графике 3 имеет лучшие характеристики, чем «критическая» ПХ, представленная на графике 2. С учетом минимальных значений функции Dx (Т2) выберем Т2 = 25 мс. При этом (после уточнения с помощью рассмотренных выше функций и команд «MathCad») получим следующие параметры качества ПХ: Тр = 90 мс, Тmax1 = 51 мс, hmax = 1,25 (γ = 25%), Тзап = 15 мс, Т01 = 5,2 мс, Т09 = 25 мс, d h (Тзап)/d t (скорость нарастания фронта) = 40 В/с.
На рис. 7.14 представлены графики АЧХ и ФЧХ. График 1 (штриховая линия) соответствует неоптимизированной системе (Т2 = 4,7 мс). График 2 (сплошная линия) построен при Т2 = 25 мс. Из рис. 7.14 видно, что до оптимизации РАС имела существенный резонансный выброс (график 1 – штриховая линия) и, как следствие, сильно колебательный характер ПХ. После оптимизации величина выброса существенно уменьшилась (график 2 – сплошная линия). После оптимизации РАС запасы устойчивости увеличились и составили: по усилению – Аз2 = 80 дБ, по фазе – j з2 = 49° (исходные значения: Аз1 = 40 дБ и по фазе j з1 = 12°). При необходимости можно было бы включить в оптимизационную задачу и другие параметры РАС (Sд, k0 , k2, Т1, Т2), что повысило бы эффективность оптимизации, хотя и существенно усложнило бы решение.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.195 (0.006 с.) |



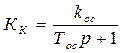 ;
; .
. , kэкв = 1/ kос, Tэкв = 1/(k0kос). (7.7)
, kэкв = 1/ kос, Tэкв = 1/(k0kос). (7.7) ) на безынерционное (W(p) = k0) и интегрирующее (W(p) = k0 / p) звенья.
) на безынерционное (W(p) = k0) и интегрирующее (W(p) = k0 / p) звенья. , (7.8)
, (7.8)
 , (7.9)
, (7.9) РАС становится невосприимчивой к ошибке. В результате можно повысить точность РАС без ухудшения устойчивости.
РАС становится невосприимчивой к ошибке. В результате можно повысить точность РАС без ухудшения устойчивости. 7.2. Рассмотрим пример синтеза схемы по заданной асимптотической ЛАЧХ [6, 17] по следующим исходным данным: L(0) = 60 дБ, w с1 = 10, w с2 = 100, w с3 = 3000 (рад/с),
7.2. Рассмотрим пример синтеза схемы по заданной асимптотической ЛАЧХ [6, 17] по следующим исходным данным: L(0) = 60 дБ, w с1 = 10, w с2 = 100, w с3 = 3000 (рад/с), . (7.10)
. (7.10) На рис. 7.8 сплошной линией приведена ЛАЧХ синтезированной схемы (31). Штриховой линией на рис. 7.8 показана заданная асимптотическая ЛАЧХ. Отклонения асимптотической ЛАЧХ от точной в области частот среза не превышают 3 дБ.
На рис. 7.8 сплошной линией приведена ЛАЧХ синтезированной схемы (31). Штриховой линией на рис. 7.8 показана заданная асимптотическая ЛАЧХ. Отклонения асимптотической ЛАЧХ от точной в области частот среза не превышают 3 дБ.
 Повышая значение R7 со 100 до 150 кОм отклонение ЛАЧХ от заданной на w =1 можно снизить до 1 дБ.
Повышая значение R7 со 100 до 150 кОм отклонение ЛАЧХ от заданной на w =1 можно снизить до 1 дБ. Отклонения от заданной (штриховая линия на рис. 7.10) максимальны на w < 1 и не превышают 3 дБ.
Отклонения от заданной (штриховая линия на рис. 7.10) максимальны на w < 1 и не превышают 3 дБ.

 , а возмущение – подобно ФВЧ
, а возмущение – подобно ФВЧ  . При расширении полосы пропускания увеличивается составляющая ошибки по возмущению (помехе), но уменьшается составляющая ошибки по управляющему воздействию.
. При расширении полосы пропускания увеличивается составляющая ошибки по возмущению (помехе), но уменьшается составляющая ошибки по управляющему воздействию. ) и постоянные времени фильтров (Ti).
) и постоянные времени фильтров (Ti). по параметрам T и k2 [1, 18] при квадратичном воздействии λ(t) = λ 2t² ×1(t) и белом шуме на выходе дискриминатора со спектральной плотностью ξ(t) = S ξ(0) = N0.
по параметрам T и k2 [1, 18] при квадратичном воздействии λ(t) = λ 2t² ×1(t) и белом шуме на выходе дискриминатора со спектральной плотностью ξ(t) = S ξ(0) = N0. . (7.11)
. (7.11) . (7.12)
. (7.12) . (7.13)
. (7.13) . (7.14)
. (7.14) ; (7.15)
; (7.15) . (7.16)
. (7.16) ;
;  . (7.17)
. (7.17) На рис. 7.12 представлен график зависимости дисперсии от Т2, построенный по формуле (6.19) или с использованием формулы (6.25).
На рис. 7.12 представлен график зависимости дисперсии от Т2, построенный по формуле (6.19) или с использованием формулы (6.25).




