
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды элементарных динамических звеньевСодержание книги
Поиск на нашем сайте Математическая модель системы может быть представлена либо уравнением, либо в виде структурной схемы. Основным элементом такой схемы является динамическое звено. Этим названием подчеркивается инерционность звеньев, то есть их реакция на входное воздействие с некоторым опозданием. Динамическое звено – элемент системы обладающий свойствами однонаправленности и независимости. Число динамических звеньев структурной схемы не обязательно равно количеству блоков в системе, а определяется удобством математического описания и анализа системы в целом. На практике ПФ РАС представляет собой произведение передаточных функций динамических звеньев, порядок полинома порядок передаточной функции, которой не выше второго. K (p) = где Т – постоянная времени звена, z – коэффициент демфирования (относительный коэффициент затухания, обратная величина добротности резонансной системы), v – количество интеграторов (показатель астатизма системы). В числителе (2.20) собираются множители с опережением по фазе (дифференцирование), в знаменателе (2.20) – с отставанием по фазе (интегрирование). Полиномы первого порядка соответствуют звеньям первого порядка, полиномы второго порядка – звеньям второго порядка. Динамические звенья разделяют на интегрирующие, дифференцирующие и позиционные звенья. Характеристики элементарных звеньев (схема, ПФ, ПХ, ИХ) и их частотные и временные графики приведены в прил. 2. К позиционным звеньям относят · звенья пропорционального регулирования (ПФ · апериодические (ПФ · колебательные (ПФ · безынерционные (ПФ K (p) = k0). К интегрирующим звеньям относятся · идеальные интеграторы (ПФ · инерционные интеграторы (ПФ · замедляющие (апериодические) (ПФ · изодромные (ПФ К дифференцирующим относят · идеально дифференцирующие (K (p) = k0p), · дифференцирующие с замедлением (ПФ · форсирующие звенья (ПФ K (p) = k0 (1 + Tp)). (2.21) Так же выделяют звенья с чистым запаздыванием (на время t): f (t) «F (p) = K (p) Þ K (p) = e–p τ «f (t – τ). (2.22) При экспериментальных исследованиях динамических звеньев используют типовые испытательные сигналы. При этом необходимо оценить ограничение, которое необходимо наложить на реальный испытательный сигнал. Дельта-функцию d(t) при экспериментальном определении ИХ можно заменить коротким импульсом, при этом необходимо, чтобы его длительность была на 1–2 порядка меньше времени задержки цепи. При определении ПХ аналогичные требования предъявляются к времени нарастания фронта импульса, реализующего действие единичной функции 1(t). 2.5. Правила структурных преобразований При анализе сложных схем для получения ПФ системы в целом удобно использовать правила структурных преобразований, которые позволяют упростить схему РАС и расчеты ее характеристик. 1. Каскадное соединение (рис. 2.6):
2. Суммирование звеньев (рис. 2.7):
3. Звено с обратной связью (ОС) (рис. 2.8): После преобразований для звена с ОС получаем
4. Перенесение сумматора. Рассмотрим перенос сумматора влево и вправо от исходной точки включения и дополним схему таким образом, чтобы ПФ системы по входному воздействию (K λ y (p) = K1 (p) K2 (p)) и возмущению (K ξ y (p) = = K2 (p)) не изменилась.
Таким образом, при переносе сумматора влево для сохранения тех же ПФ РАС необходимо добавить в цепь воздействия или возмущения, входящего в сумматор, звено с ПФ K (p) = 1/ K1, а при переносе вправо – звено с ПФ K (p) = K2. 5. Перенесение точки разветвления. Рассмотрим перенос точки разветвления влево и вправо от исходной точки включения и дополним схему таким образом, чтобы ПФ системы по входному воздействию (K λ y1 (p) = K1 (p) K2 (p) и K λ y2 (p) = K1 (p) K3 (p)) не изменилась.
Таким образом, при переносе точки разветвления влево для сохранения тех же ПФ РАС необходимо добавить в цепь разветвления звено с ПФ K (p) = K1, а при переносе вправо – звено с ПФ K (p) = 1/ K2. Пример 2.1. Упростить схему, показанную на рис. 2.9. Выделим соединения, допускающие упрощение. Звенья с K2 и K3 соединены каскадно, что позволяет заменить их одним звеном с K23 = K2 × K3. Звенья с K4 и K5 имеют обратную связь, что позволяет заменить их одним звеном с K45 = K4 /(1+ K4 × K5). ПФ полученных звеньев следует сложить на сумматоре перед звеном с K6, а затем полученное звено (его ПФ K25 = K23 + K45) каскадно соединяется с K6, что в результате дает K26 = [ K2 × K3 + K4 /(1+ K4 × K5)]× K6 = K2 × K3 × K6 + K4 × K6 /(1+ K4 × K5). (2.26) В результате получаем схему, показанную на рис. 2.10
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

 , (2.20)
, (2.20) ),
), , w < wс1),
, w < wс1),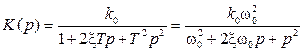 ),
), ),
), ),
), , w > wс1) и
, w > wс1) и ) звенья.
) звенья.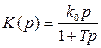 ) и
) и Итоговая ПФ каскадного соединения К å (соответственно L å(w)) имеет вид:
Итоговая ПФ каскадного соединения К å (соответственно L å(w)) имеет вид: 
 ,
, 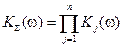 ,
,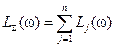 . (2.23)
. (2.23)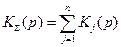 ,
,  . (2.24)
. (2.24)
 (для положительной ОС) и
(для положительной ОС) и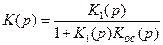 (для отрицательной ОС). (2.25)
(для отрицательной ОС). (2.25)






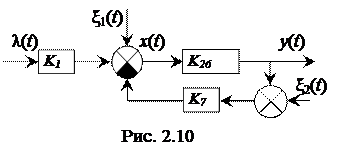 Эту схему можно упрощать и дальше: перенести сумматор с ξ2(t) к точке приложения ξ1(t), преобразовать обратную связь звеньев с K26 и K7, но можно и по этой схеме определить ПФ выходного процесса и ПФ ошибки по входному воздействию λ(t) и возмущениям ξ1(t), ξ2(t) с помощью формул следующего параграфа.
Эту схему можно упрощать и дальше: перенести сумматор с ξ2(t) к точке приложения ξ1(t), преобразовать обратную связь звеньев с K26 и K7, но можно и по этой схеме определить ПФ выходного процесса и ПФ ошибки по входному воздействию λ(t) и возмущениям ξ1(t), ξ2(t) с помощью формул следующего параграфа.


