
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь ачх и фчх замкнутой и разомкнутой системСодержание книги
Похожие статьи вашей тематики
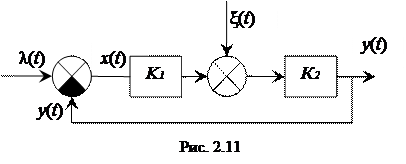
Поиск на нашем сайте Для анализа РАС необходимо представить входное воздействие λ(t), возмущение ξ(t), ошибку x (t) в операторной форме, а затем получить ПФ разомкнутой и замкнутой систем по воздействию L(p), по возмущению X(p), и по ошибке Кх (p).
Многие РАС могут быть сведены к обобщенной структурной схеме, показанной на рис. 2.11. ПФ разомкнутой системы определяется формулой
ПФ замкнутой системы по входному воздействию с учетом (2.27):
ПФ разомкнутой системы через ПФ замкнутой системы определяется так:
ПФ замкнутой системы по возмущению с учетом (2.28):
ПФ замкнутой системы по ошибке:
Пример 2.2. Определим ПФ выходного процесса и ПФ ошибки по входному воздействию λ(t) и возмущениям ξ1(t), ξ2(t) для схемы, показанной на рис. 2.10, которая была получена в примере 2.1 упрощением исходной схемы. С помощью формул (2.28) и (2.30) получаем:
Для представления процессов через ПФ звеньев исходной схемы (рис. 2.9) необходимо в полученных выражениях заменить K26 по формуле (2.26). Определим связь ПФ разомкнутой W (p) и замкнутой H (p) систем по воздействию (5.1), сделаем замену переменных p ® i w, и выделим модуль и аргумент:
После преобразований получим:
Выделим вещественную и мнимую части: Re: Найдем связь АЧХ и ФЧХ разомкнутой и замкнутой систем.
Выражения (2.35) – (2.36) можно записать через переменную
Из выражений (2.35) – (2.38) следует, что в диапазоне частот, где W (ω) > 1, АЧХ замкнутой системы H (ω) примерно равна единице, а ФЧХ почти не отличается от нуля. В диапазоне частот, в котором W (ω) < 1, характеристики замкнутой системы (АЧХ и ФЧХ) стремятся к характеристикам разомкнутой системы.
Найдем связь годографов разомкнутой и замкнутой систем. Пусть
Связь с ПХ замкнутой РАС определяется формулами [10]:
При сложном входном воздействии формулы (2.40) можно использовать при вычислениях с помощью интеграла Дюамеля (свертки). Установившееся значение выходного сигнала системы вычисляется по теореме о конечном значении:
где H (р) – передаточная функция замкнутой системы.
В астатических РАС установившееся значение выходного сигнала равно ууст = H (0) = 1, а в статических – ууст = H (0) = k0 /(1 + k0). Список рекомендуемой литературы: [ 1, с. 27-28, 34-36; 3, с. 49-52, 58-69, 90-93, 104-107, 123-124, 499-513; 4, с. 25-33, 42-48; 5, с. 39-45, 152; 7, с. 19-50; 10, т. 1, с. 37-52, 77-81, 86-92; 11, с. 310-330, 485-489; 13; 18, с. 31-38; 27, с. 17-24]. Контрольные вопросы 1. Дайте определение передаточной функции системы по ошибке, входному и возмущающему воздействиям. 2. Как из ПФ можно получить АЧХ и ФЧХ? 3. Дайте определение ПХ и ИХ. 4. Как из ПФ получают ПХ и ИХ? 5. Как в экспериментальных исследованиях можно смоделировать функции Дирака (дельта-функция) и Хевисайда (единичный скачок)? 6. Назовите правила структурных преобразований. 7. Дайте определение динамическому звену. 8. Какую погрешность допускают, применяя асимптотические ЛАЧХ и ЛФЧХ вместо точных ЛАЧХ и ЛФЧХ? 9. В чем достоинства асимптотических ЛАЧХ и ЛФЧХ? 10. Какая связь существует между характеристиками разомкнутой и замкнутой систем? 11. Дайте характеристику основным разновидностям динамических звеньев. 12. Опишите особенности частотных характеристик основных разновидностей динамических звеньев. 13. Опишите особенности временных характеристик звеньев основных типов. 14. Какая связь существует между АЧХ и ПХ РАС?
Обобщенная следящая система. Функциональные схемы и принцип действия Основных разновидностей рас
Принципы действия основных разновидностей РАС. Обобщенные функциональная и структурная схемы (математические модели) следящих РАС. Основные элементы обобщенной РАС. Уравнения замкнутой следящей системы относительно выходного процесса и ошибки слежения. ПФ замкнутой РАС по ошибке и по возмущению. Основные элементы РАС и их математическое описание. Дискриминаторы и их статические эквиваленты. Дискриминационная и флуктуационная характеристики дискриминаторов. Математическая модель дискриминатора и условия его линейного и стационарного описания. Объекты управления РАС. Функциональные схемы и математическое описание РАС, сведение их к обобщенной следящей системе. Системы частотной автоподстройки частоты (ЧАП). Системы фазовой автоподстройки частоты (ФАПЧ). Слежение за частотой и фазой сигнала. Системы стабилизации частоты и фазы сигнала. Системы автоматической регулировки (стабилизации) усиления (АРУ). Системы слежения за временным положением импульсов. РАС углового сопровождения цели. Системы сопровождения по дальности. РАС настройки и подстройки контуров.
|
|||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

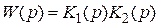 . (2.27)
. (2.27)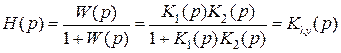 . (2.28)
. (2.28)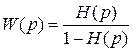 . (2.29)
. (2.29)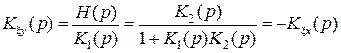 . (2.30)
. (2.30)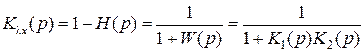 . (2.31)
. (2.31)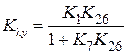 ,
, 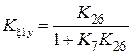 ,
, 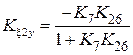 ;
;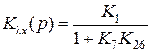 ,
, 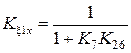 ,
, 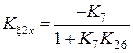 .
.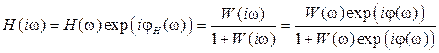 . (2.32)
. (2.32)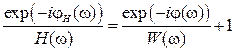 . (2.33)
. (2.33)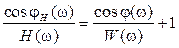 , Im:
, Im: 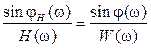 . (2.34)
. (2.34)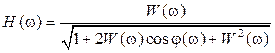 , (2.35)
, (2.35)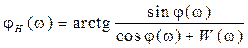 . (2.36)
. (2.36)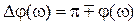 , связанную с запасом РАС по фазе:
, связанную с запасом РАС по фазе: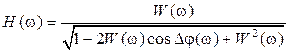 , (2.37)
, (2.37)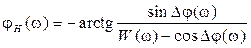 . (2.38)
. (2.38)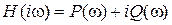 , а
, а 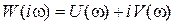 , тогда из (2.32) получим:
, тогда из (2.32) получим: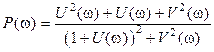 ,
, 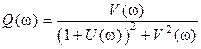 . (2.39)
. (2.39)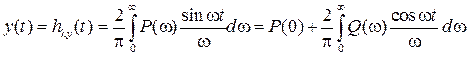 . (2.40)
. (2.40)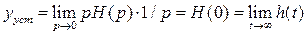 , (2.41)
, (2.41)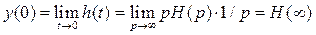 , (2.42)
, (2.42)


