
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статические и динамические характеристики РАССодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статическая характеристика отражает функциональную зависимость выходной величины от входного воздействия в установившемся режиме. Большинство реальных звеньев и узлов РАС имеют нелинейные статические характеристики, то есть отношение выходной величины к входной в стационарном режиме зависит от уровня входного воздействия. Статическая характеристика звена может деформироваться при действии на него возмущений, тогда говорят о семействе статических характеристик (см. рис. 1.3). Многие звенья в определенном интервале входных воздействий можно приближенно считать линейными, поэтому при их экспериментальном исследовании на первый план выдвигается задача отыскания границ этого интервала. Так, например, статическая характеристика двухстороннего ограничителя будет линейна в диапазоне входных напряжений Uвх ≤ Uпор (рис. 2.1). Такую статическую характеристику можно аппроксимировать выражением Uвых =
Uвых = Umax при Uвх ≥ Uпор.
Величину k можно определить и по динамическим характеристикам. К динамическим относят частотные и временные характеристики. Частотные характеристики показывают изменения модуля и (или) аргумента комплексного коэффициента передачи в функции от частоты гармонического входного воздействия. Аргумент временных характеристик – время. Свойства линейного динамического звена (как и всей системы) могут быть количественно и качественно описаны через его ПФ. Передаточная функция (ПФ). Различают ПФ в операторной форме, в форме изображений Лапласа и частотные ПФ. Из-за наличия инерционных элементов и преобразований энергии процессы в РАС (рис. 2.2) обычно описываются дифференциальными уравнениями:
Используя оператор дифференцирования p = d/dt, удобно записать уравнение (2.1) в операторной форме (y ( n ) → pn):
Взяв отношение
ПФ в форме изображений Лапласа Kyx (p) называют отношение изображения Лапласа выходного процесса Y (p) к изображению Лапласа входного воздействия X (p) при нулевых начальных условиях
где L – оператор прямого преобразования Лапласа:
Нулевые начальные условия означают, что на момент включения запасы энергии в системе (например, заряды конденсаторов) отсутствуют. У минимально фазовых цепей все коэффициенты полиномов положительные, у неминимально фазовых цепей могут быть отрицательные коэффициенты. У физически реализуемой РАС порядок полиномов в знаменателе должен быть больше порядка полиномов в числителе (n < m). От ПФ в операторной форме можно перейти к частотной ПФ (ЧПФ), заменив оператор p на переменную i w, где
Y (i w) – спектральная характеристика выходного процесса, полученная как прямое преобразование Фурье F [ y (t)] от временной функции y (t)
Замена Kyx (p) на Kyx (i w) правомерна только для стационарных режимов. ЧПФ – комплексный коэффициент передачи системы по частоте w. Частотные свойства ЧПФ отображают также в виде графика – годографа. Годограф ЧПФ строят либо в полярной, либо в декартовой системе координат. При этом соответственно пользуются экспоненциальной или алгебраической формами записи комплексного числа
Соответствующий график содержит информацию о модуле – Kyx (ω), фазе – φ yx (ω) и циклической частоте ω, так как каждая его точка соответствует определенной фиксированной частоте, поэтому его называют амплитудно-фазо-частотной характеристикой (АФЧХ). Амплитудно-частотная характеристика (АЧХ) строится по формуле
где Y (ω) и X (ω) – комплексные амплитуды процессов на частоте ω. Фазо-частотная характеристика (ФЧХ) представляется в виде
Графики АЧХ и ФЧХ имеют линейный масштаб по оси абсцисс. Временные характеристики. T – постоянная времени цепи, которая характеризует инерционность (быстродействие) звена, ее можно определить и графически, если провести касательную к кривой h (t) (ПХ) в точке h (0) (см. рис. 2.3).
При исследовании ПХ динамических звеньев в виде электрических цепей создать единичное ступенчатое воздействие (скачок) напряжения (тока) несложно. Для этого, в частности, можно использовать периодическую последовательность прямоугольных импульсов со скважностью равной 2 (меандр). Однако искажений ПХ не будет лишь в том случае, когда длительность импульса Ти будет больше Tpег звена. Амплитуда импульсов должна быть выбрана с таким расчетом, чтобы не нарушились условия линейности звена. Импульсная характеристика (ИХ) – g (t) определяет поведение процесса на выходе системы при воздействии на ее входе дельта-импульса (d(t) – функции Дирака) при нулевых начальных условиях.
обратное преобразование Лапласа ПФ K (p); а
обратное преобразование Фурье ЧПФ K (i w). ИХ, как и ПХ h (t), АФЧХ, совокупность ЛАЧХ и ЛФЧХ, также позволяет определить все параметры линейного звена, составить его ПФ и дифференциальное уравнение. Однако при экспериментальном исследовании g (t)возникает сложность в моделировании дельта-импульса, так как по определению он должен иметь бесконечно большую амплитуду при бесконечно малой длительности. В условиях эксперимента можно сформировать воздействие d(t) лишь приближенно, например, смоделировать d(t) коротким импульсом, длительность которого должна быть много меньше постоянной времени звена, определяющего его быстродействие (Ти << Т). Рекомендуется выбирать Ти из отношения Ти < Т /(20…50). (2.13) Амплитуда импульса должна соответствовать предельным возможностям звена по линейности статической характеристики.
|
|||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 677; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.177 (0.01 с.) |

 kUвх при Uвх ≤ Uпор ,
kUвх при Uвх ≤ Uпор ,
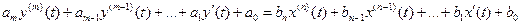 . (2.1)
. (2.1)
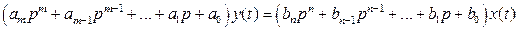 . (2.2)
. (2.2) , получим ПФ Kyx(p) в операторной форме, отражающую способность звена преобразовывать входное воздействие.
, получим ПФ Kyx(p) в операторной форме, отражающую способность звена преобразовывать входное воздействие. . (2.3)
. (2.3) , (2.4)
, (2.4) . (2.5)
. (2.5) – мнимая единица.
– мнимая единица.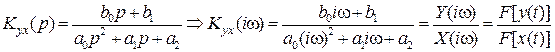 . (2.6)
. (2.6)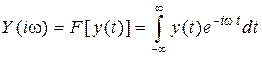 . (2.7)
. (2.7) . (2.8)
. (2.8) , (2.9)
, (2.9) . (2.10)
. (2.10) Для звеньев первого порядка время регулирования может быть определено как Tpег= (4...5) T [17].
Для звеньев первого порядка время регулирования может быть определено как Tpег= (4...5) T [17].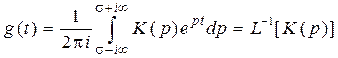 – (2.11)
– (2.11) – (2.12)
– (2.12)


