
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные характеристики интегрирующих систем.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
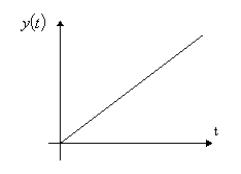
Идеальное интегрирующее звено. Звено описывается дифференциальным уравнением:
Его кривая разгона:
передаточная функция:
амплитудно-фазовая характеристика:
амплитудно-частотная характеристика:
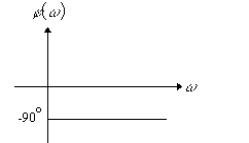
фазочастотная характеристика:
На рис. 47 и 48 приведены временные, а на рис. 49, 50, 51 – частотные характеристики идеального интегрирующего звена.
Рис.47. Кривая разгона
Рис.48. Импульсная переходная функция
Рис. 49. Амплитудно-фазовая характеристика
Рис. 50. Амплитудно-частотная характеристика
Рис. 51. Фазочастотная характеристика Реальное интегрирующее звено Звено описывается дифференциальным уравнением:
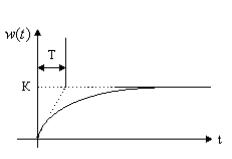
Его кривая разгона:
импульсная переходная функция:
передаточная функция:
амплитудно-фазовая характеристика:
амплитудно-частотная характеристика:
фазочастотная характеристика:
На рис. 53, 54, 55, 56, 57 приведены соответственно кривая разгона, импульсная переходная функция, АФХ, АЧХ и ФЧХ идеального интегрирующего звена. Примером такого звена является двигатель (рис. 58). Уравнение двигателя, приведенного на рис. 58, можно записать в виде:
где T– постоянная времени двигателя, k – коэффициент передачи.
Рис. 53. Кривая разгона
Рис. 54. Импульсная переходная функция
Рис. 55. Амплитудно-фазовая характеристика
Рис. 56. Амплитудно-частотная характеристика
Рис. 57. Фазочастотная характеристика
Рис. 58. Реальное интегрирующее звено: X – управляющее воздействие (например, подводимое напряжение
где Y – приведенный к валу двигателя суммарный момент инерции;
20.Частотные характеристики статических систем. Системы в которых в своей структуре не содержится последовательно присоединенного интегрирующего звена называют статическими. Примером статических систем служат последовательно соединенные звенья с передаточными функциями:
Система в структуре которой имеется последовательное соединённое интегрирующее звено называется астатической. Если к данному примеру прибавить
В знаменателе появляется множитель в компл. переменной «р». Последовательное присоединение еще одного интегр. Звена изменит множитель на « Пример. Передаточная функция неизменяемой части САР:
– действительная часть:
– мнимая часть:
Амплитудно-частотная характеристика описывается выражением:
. Рисунок 2 - Амплитудно-частотная характеристика
Фазовая частотная характеристика описывается выражением:
Рисунок 3 - Фазовая частотная характеристика
Применение изодромных устройств Существует путь повышения порядка ас-татизма системы без заметного или недопустимого ухудшения ее запаса устойчивости. Этот путь заключается в применении изодромных устройств, например таких, как изображенные па рис. 4.19. Структурная схема системы при введении изодром-ного устройства изображена па рис. 9.4. Передаточная функция изодромного устройства может быть представлена в виде
ЧХ систем с обратной связью Обратная связь может быть как положительной, так и отрицательной. Отрицательная обратная связь (ООС) действует в сторону уменьшения отклонений текущих значений координат объекта от их предшествующих значений, а положительная обратная связь (ПОС) действует в сторону увеличения. Следовательно, ООС позволяет строить наиболее точные САУ, так как несёт в себе информацию обо всех изменениях регулируемой величины; ПОС служит для изменения внутренних свойств отдельных звеньев САУ. Соединение обратной связью
Если задана передаточная Функция W(S), то путём подставки S=jw получаем частотную передаточную функцию W (jw), которая является комплексным выражением т.е.
А(w) – вещественная составляющая К(w) – мнимая составляющая. Частотная передаточная функция может быть представлена в показательной форме
Функция М(w), представленная при изменении частоты от 0 до Ґ получило название амплитудной частотной характеристики (АЧХ).Функция j(w), представленная при изменении частоты от 0 до Ґ называется фазовой частотной характеристикой (ФЧХ). Для анализа поведения системы в большом диапазоне частот удобно в качестве аргумента частотных характеристик рассматривать не частоту ω, а ее десятичный логарифм ω 10 log.
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1080; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 .
. ,
, ,
, ,
, ,
, .
.



 .
. ,
, ,
, ,
, ,
, ,
, .
. ,
,






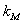 – коэффициент пропорциональности между управляющим воздействием X и выдающим моментом M;
– коэффициент пропорциональности между управляющим воздействием X и выдающим моментом M; – соответственно пусковой момент и скорость холостого хода двигателя при некотором значении управляющего воздействия.
– соответственно пусковой момент и скорость холостого хода двигателя при некотором значении управляющего воздействия.



 ».
».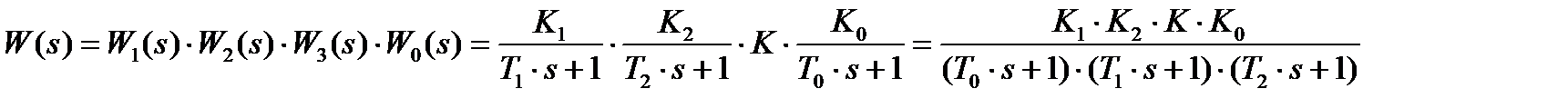 Переведем передаточную функцию разомкнутой системы в комплексные числа, то есть выделим действительную и мнимую части.
Переведем передаточную функцию разомкнутой системы в комплексные числа, то есть выделим действительную и мнимую части.

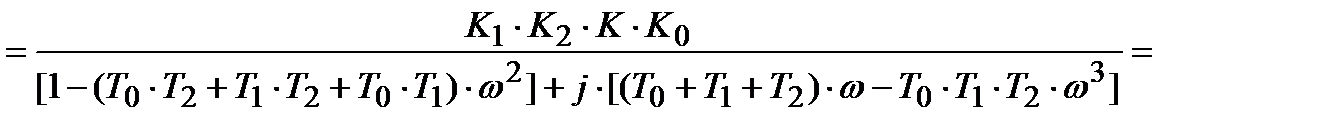


 .
.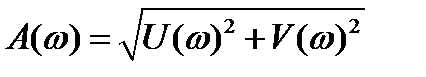

 .
.








