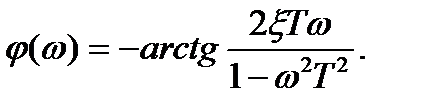Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные характеристики типовых звеньев.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте К простейшим типовым звеньям относятся: · усилительное, · инерционное (апериодическое 1-го порядка), · интегрирующие (реальное и идеальное), · дифференцирующие (реальное и идеальное), · апериодическое 2-го порядка, · колебательное, · запаздывающее.
Частотные характеристики звена определяют его реакцию на гармонический входной сигнал в установившемся режиме (т.е. после завершения переходных процессов). Частотной характеристикой динамического звена называют функцию комплексного аргумента jw, полученную путем формальной замены s на jw в выражении передаточной функции Получим связь частотной характеристики с известными понятиями. Для этого рассмотрим динамическое звено с передаточной функцией W(s) и сигналами, Получим отношение спектров - Таким образом, частотную характеристику динамического звена можно определить как отношение спектра (преобразования Фурье) выходного сигнала к спектру входного сигнала. Знание частотной характеристики звена позволяет определить выходной спектр по входному
Рассмотрим динамическое звено –
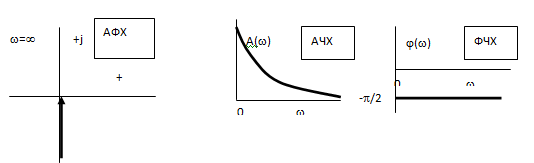
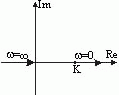
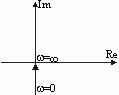
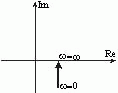
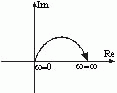
Получим спектр выходного сигнала – импульсной характеристики Рассмотрим передаточную функцию, состоящую из n-го количества элементов. Последовательность выражений позволяет найти амплитуду и фазу колебаний на выходе системы при гармоническом воздействии на ее входе. Модуль этого выражения показывает, во сколько раз увеличивается или уменьшается амплитуда колебаний на выходе системы по сравнению с амплитудой колебаний на входе. Аргумент вектора F(jω) описывает фазовый угол колебаний по отношению колебаниям на входе => (*) определяет частотную характеристику, называемую амплитудно-фазовой частотной характеристикой (АФЧХ). АФЧХ строится на комплексной плоскости
АФЧХ: Вещественные или мнимые частотные характеристики связаны с АЧХ и ФЧХ следующим образом:
При анализе САР на устойчивость и качества процесса регулирования, а также при решении других задач, часто обращаются к ЛЧХ Усиление L(ω) = 20lg|Ф(jω)| = 20lgA(ω) [дБ] – является единицей логарифмической относительно величины. Изменения относительно двух величин в 10 раз соответствует изменению усиления на 20 дБ. Известно, что АЧХ представляет собой отношение 2-х амплитуд: входного и выходного сигналов.
Версия по Петрову: К простейшим типовым звеньям относятся: · усилительное, · инерционное (апериодическое 1-го порядка), · интегрирующие (реальное и идеальное), · дифференцирующие (реальное и идеальное), · апериодическое 2-го порядка, · колебательное, · запаздывающее.
Частотные характеристики усилительного звена можно получить по его передаточной функции, при этом АФХ, АЧХ и ФЧХ определяются следующими соотношениями:
Частотные характеристики интегрирующего звена определяются соотношениями:
Колебательное звено Амплитудно-фазовая частотная характеристика (АФХ) имеет вид и определяется соотношением
Амплитудно-частотные характеристики (АЧХ) для различных значений x имеет вид (рис. 22б) и определяется соотношением
Фазовая частотная характеристика (ФЧХ) имеет вид и определяется соотношением
Частотные характеристики колебательного звена имеют вид
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 903; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |


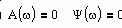
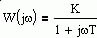





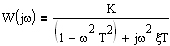
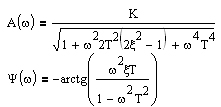



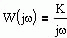
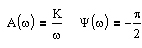








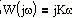



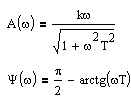



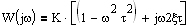


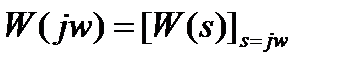

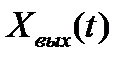 . Пусть,
. Пусть,  .
.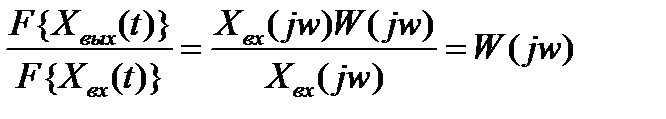
 .
.
 Тогда имеем
Тогда имеем  , то есть преобразование Фурье от импульсной характеристики равно частотной характеристике динамического звена.
, то есть преобразование Фурье от импульсной характеристики равно частотной характеристике динамического звена.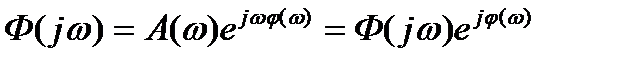 j – мнимая единица.
j – мнимая единица. - коэффициент, характеризующий изменение амплитуды при изменении частоты, при изменяющейся частоте, называется амплитудно-частотной характеристикой (АЧХ).
- коэффициент, характеризующий изменение амплитуды при изменении частоты, при изменяющейся частоте, называется амплитудно-частотной характеристикой (АЧХ).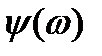 дает представление о фазовом сдвиге выходных колебаний и он называется фазово-частотной характеристикой (ФЧХ)
дает представление о фазовом сдвиге выходных колебаний и он называется фазово-частотной характеристикой (ФЧХ)
 .
.