Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмические частотные характеристикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Частотные характеристики достаточно сложно строить вручную. В 60-е годы, когда раз-вивалась классическая теория управления, не было мощных компьютеров, поэтому наиболь-шую популярность приобрели приближенные методы, с помощью которых можно было проек-тировать регуляторы с помощью ручных вычислений и построений. Один из таких подходов основа на использовании логарифмических частотных характеристик.
Вместо A (ω) было предложено использовать логарифмическую амплитудную частотных характеристику (ЛАЧХ):график,на котором по оси абсцисс откладывается десятичный лога-рифм частоты (lg ω), а по оси ординат – величина Lm (ω) = 20 lg A (ω), измеряемая в децибелах
(дБ). При построении логарифмической фазовой частотной характеристики (ЛФЧХ) по оси абсцисс также откладывается логарифм частоты lg ω.
Единицей отсчета на логарифмической оси частот является декада – диапазон, на котором частота увеличивается в 10 раз (а значение ее логарифма увеличивается на единицу). Вместе ЛАЧХ и ЛФЧХ называются логарифмической амплитудно-фазовой частотной характеристикой (ЛАФЧХ) или диаграммой Боде.
Логарифмические характеристики обладают двумя ценными свойствами:
© К.Ю. Поляков, 2008
1) ЛАЧХ и ЛФЧХ для произведения W 1 (s) W 2 (s) вычисляются как суммы ЛАЧХ и ЛФЧХ отдельных звеньев:
2) в области высоких и низких частот ЛАЧХ асимптотически приближаются к прямым, наклон которых составляет ± 20 дБ/дек (децибел на декаду), ± 40 дБ/дек и т.д.
В классической теории управления хорошо разработаны методы анализа и синтеза систем на основе асимптотических ЛАЧХ, которые представляют собой ломаные линии и легко стро-ятся вручную. C появлением компьютерных средств расчета практическая ценность ЛАФЧХ несколько снизилась, однако они по сей день остаются простейшим инструментом прикидоч-ных расчетов для инженера.
W (s)= Ts 1+1при T =1с.
Первая асимптота, определяющая поведение ЛАЧХ на низких частотах, имеет нулевой на-клон, потому что звено относится к классу позиционных звеньев, имеющих постоянный ненуле-вой статический коэффициент усиления, то есть
W (0)=1≠0.
Если W (0) = 0, передаточная функция содержит множитель sk (k > 0), который соответ-
ствует производной порядка k. В этом случае наклон ЛАЧХ на низких частотах равен k ⋅20дБ/дек.
Если W (0) = ∞, звено содержит один или несколько интеграторов, то есть в знаменателе
есть сомножитель sk. Тогда наклон ЛАЧХ на низких частотах равен − k ⋅20 дБ/дек. Наклон ЛАЧХ на высоких частотах определяется разностью степеней числителя и зна-менателя передаточной функции. Если числитель имеет степень m, а знаменатель – степень n, то наклон последней асимптоты равен 20 ⋅(m − n) дБ/дек. В нашем примере m − n = 0 −1 = −1.
Поэтому вторая асимптота, определяющая свойства звена на высоких частотах, имеет наклон − 20 дБ/дек, то есть, за одну декаду значение уменьшается на 20 дБ (проверьте по графику!).
© К.Ю. Поляков, 2008
Типовые динамические звенья
Обычно система управления состоит из отдельных блоков, каждый из которых описыва-ется уравнениями низкого порядка (чаще всего – первого или второго). Для понимания работы системы в целом желательно хорошо представлять, как ведут себя ее отдельные элементы. Кроме того, при построении ЛАФЧХ сложной системы передаточную функцию разбивают на простейшие сомножители
W (s) = W 1 (s) ⋅ W 2 (s)...⋅ WN (s) и далее, воспользовавшись свойствами ЛАФЧХ, строят характеристики для всей системы как суммы ЛАЧХ и ЛФЧХ отдельных звеньев.
Усилитель
Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то есть W (0) = k ≠ 0, называются позиционными. Это значит, что числитель и знаменатель переда-
точной функции имеют ненулевые свободные члены (постоянные слагаемые).
Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его переда-точная функция W (s) = k. Строго говоря, он не является динамическим звеном, поскольку из-
менение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала 1 (t) (или дельта-функции δ (t)) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны h (t)= k (t >0)и w (t)= k ⋅ δ (t).
Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в k раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала:
A (ω)= k, φ (ω)=0.
Апериодическое звено
Одно из самых часто встречающихся звеньев – апериодическое, которое описывается дифференциальным уравнением
и имеет передаточную функцию W (s) = Tsk +1. Здесь k – безразмерный коэффициент, а T > 0 –
постоянная, которая называется постоянной времени звена. Постоянная времени – размерная величина, она измеряется в секундах и характеризует инерционность объекта, то есть скорость его реакции на изменение входного сигнала.
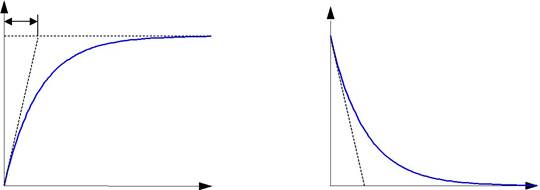
В разд. 3.3 и 3.4 мы уже нашли переходную и весовую функции апериодического звена
Они показаны на рисунке:
Колебательное звено
Колебательное звено – это звено второго порядка с передаточной функцией вида
знаменатель которой имеет комплексно-сопряженные корни (то есть, b 12 − 4 b 2 < 0). Как извест-
но из теории дифференциальных уравнений, свободное движение такой системы содержит гар-монические составляющие (синус, косинус), что дает колебания выхода при изменении входно-го сигнала. Несложно представить передаточную функцию колебательного звена в форме
В
в бесконечность) на частоте ωc, при таком входе амплитуда колебаний неограниченно растет и на практике объект разрушается.
© К.Ю. Поляков, 2008
Интегрирующее звено
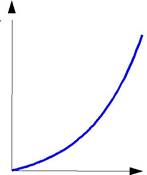
Простейший пример интегрирующего звена – ванна, в которую набирается вода. Входной сигнал – это поток воды через кран, выход системы – уровень воды в ванне. При поступлении воды уровень растет, система «накапливает» (интегрирует) входной сигнал.
Интегрирующее звено описывается уравнением
ловиях (y (0) = 0), получаем линейно возрастающую переходную характеристику: h (t)= k ⋅ t.
Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта-функции на любом интервале, включающем t = 0, равен 1. Поэтому w (t) = k (при t ≥ 0).
W (jω)= jkω = − j ωk. Можно показать,что его логарифмическая амплитудная частотная харак-
теристика – это прямая с наклоном − 20 дБ/дек. На низких частотах усиление максимально, теоретически на частоте ω = 0 оно равно бесконечности. Высокие частоты, наоборот, подавля-ются интегратором.
-90
-180
На частоте ω =1 значение ЛАЧХ равно 20 lg k, а при ω = k ЛАЧХ обращается в нуль, посколь-ку W (jω) =1. Фазовая характеристика φ (ω) = −90° – говорит о постоянном сдвиге фазы на всех частотах.
© К.Ю. Поляков, 2008
Дифференцирующие звенья
Дифференцирующее звено дает на выходе производную входного сигнала. Уравнение идеального дифференцирующего звена y (t) = k dxdt (t), его операторная запись y (t) = k ⋅ p x (t), а
передаточная функция W (s) = k ⋅ s.
Известно, что производная единичного ступенчатого сигнала 1 (t) в точке t = 0 – это дельта-функция δ (t). Поэтому переходная и весовая функции дифференцирующего звена
h (t)= kδ (t), w (t)= k dδ (t). dt Это физически нереализуемые функции, так как дельта-функцию и ее производную, имеющие бесконечные значения, невозможно получить на реальном устройстве. Поэтому идеальное диф-ференцирующее относится к физически нереализуемым звеньям.
Логарифмическая амплитудная частотная характеристика дифференцирующего звена – прямая с наклоном 20 дБ/дек, пересекающая ось абсцисс Lm (ω) = 0 на частоте ω = 1 k. При ω =1ЛАЧХ равна Lm |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1003; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |



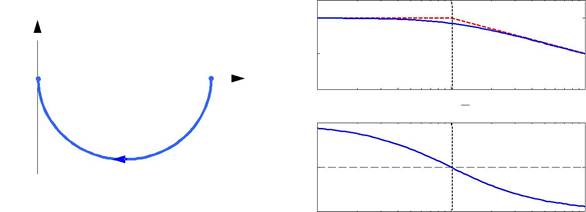
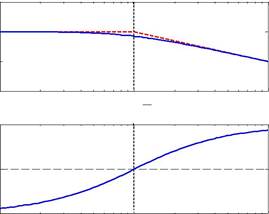
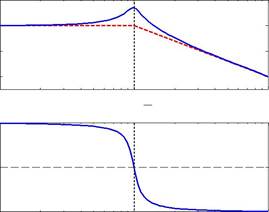
 На рисунке показаны точная (сплошная синяя линия) и асимптотическая (штриховая красная линия) ЛАФЧХ для звена первого порядка с передаточной функцией
На рисунке показаны точная (сплошная синяя линия) и асимптотическая (штриховая красная линия) ЛАФЧХ для звена первого порядка с передаточной функцией






 Интересно сравнить частотные характеристики устойчивого и неустойчивого апериодических звеньев с теми же коэффициентами усиления и постоянными времени.
Интересно сравнить частотные характеристики устойчивого и неустойчивого апериодических звеньев с теми же коэффициентами усиления и постоянными времени.






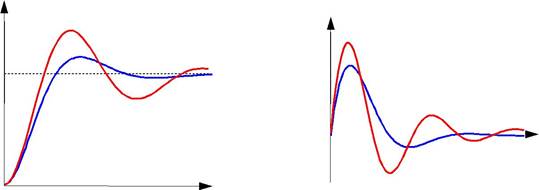
 предельном случае при ξ = 0 (консервативное звено) ЛАЧХ терпит разрыв (обращается
предельном случае при ξ = 0 (консервативное звено) ЛАЧХ терпит разрыв (обращается