Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики центра розподілу
З м і с т вступ.. 4 1. Ряди розподілу.. 4 2. Характеристики центра розподілу.. 6 3. Статистичні характеристики варіації 8 4. Дослідження асиметрії розподілу.. 11 5. Приклад.. 16 6. оформлення роботи.. 29 СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ.. 30 Вступ
Методичні вказівки призначенідля практичного освоєння теоретичного курсу статистики з теми “Ряди розподілу” на конкретному прикладі в процесі виконання курсової роботи. Письмове виконання курсової роботи сприяє не тільки поглибленому вивчанню методів статистики, але й придбанню практичних навичок з розрахунку статистичних показників, правильної побудови й оформлення таблиць, графіків. Основна мета розробок – навчити розумінню суті розрахункових показників та їхнього аналізу. Керівник курсової роботи видає студентові завдання з вихідними даними, у т.ч. - на тему “Ряди розподілу”, і встановлює порядок, обсяг і термін завершення розрахунків, аналізу і підготовки до захисту. Керівник роботи: - контролює процес виконання роботи; - рекомендує літературу і довідкові матеріали; - проводить консультації зі студентами; - допомагає в обробці вихідних даних і в складанні висновків; - перевіряє виконані розрахунки. Перед рішенням кожної задачі необхідно ретельно вивчити її зміст. Перш ніж приступати до практичного виконання завдань, варто уважно ознайомитися із відповідним матеріалом методичних вказівок та літературою з рекомендованого списку.
Ряди розподілу
Ряд розподілу – це упорядкований розподіл одиниць сукупності на групи за певною ознакою, яка варіює. Залежно від статистичної природи варіантів ряди поділяються на атрибутивні та варіаційні. Варіаційний ряд розподілу – ряд, який будується за кількісною ознакою. При складанні структурних угруповань на основі кількісних варіюючих ознак необхідно визначити кількість груп та інтервали групування. Орієнтовно оптимальну кількість груп з рівними інтервалами можна визначити за формулою американського вченого Стерджесса: n=1+3,322 lgN, де N – число одиниць сукупності. Тоді величина інтервалу:
де xmax, xmin – найбільше і найменше значення ознаки; n – кількість груп. Після визначення ознаки групування та меж груп будується ряд розподілу. Ряд розподілу характеризує склад, структуру сукупності за визначеною ознакою. Варіаційні ряди розподілу складаються з двох елементів: варіант і частот. Числові значення кількісної ознаки у варіаційному ряді розподілу називаються варіантами. Частоти - це чисельність окремих варіант кожної групи варіаційного ряду, тобто це числа, що показують як часто зустрічаються ті чи інші варіанти в ряді розподілу. Сума всіх частот складає обсяг сукупності. Частки - це частоти, виражені у виді відносних одиниць (частках чи одиниць відсотків).
Варіаційні ряди в залежності від характеру варіації підрозділяються на дискретні та інтервальні. Дискретні засновані на дискретних (перервних) ознаках, що приймає тільки цілі значення; інтервальні - на безперервних ознаках (приймаючих будь-які значення). У співвідношенні варіантів і частот виявляється закономірність розподілу. Вона описується рядом статистичних характеристик, зокрема: а) частотні характеристики; б) характеристики центра розподілу; в) характеристики варіації; г)характеристики нерівномірності розподілу, концентрації, асиметрії.
Статистичні характеристики варіації
Варіація – характеризує коливання значень ознаки, розходження значень будь-якої ознаки різних одиниць сукупності в один і той самий момент часу. Середня не показує, як розташовуються біля неї варіанти (окремі значення) ознаки. Необхідні показники, що характеризують відхилення окремих значень від загальної середньої, - показники варіації. Відносні показники варіації При порівнянні коливань різних ознак в одній і тій же сукупності, чи при порівнянні коливань значень будь-якої ознаки в декількох сукупностях з різною величиною середньої арифметичної використовують відносні показники варіації. Ці показники обчислюються як відношення абсолютних показників варіації до середньої арифметичної чи медіани. Відносні показники варіації можна отримати, використовуючи такі абсолютні показники, як абсолютний розмах варіації, середнє лінійне, середнє квадратичне і квартильное відхилення.
Коефіцієнт осциляції:
Відносне лінійне відхилення:
Коефіцієнт варіації:
Відносний показник квартильної варіації:
Найбільш часто застосовуваний показник відносної мінливості - коефіцієнт варіації. Сукупність вважається однорідною, якщо коефіцієнт варіації не перевищує 33%.
Приклад
1. Перетворимо наступні первинні дані грошового місячного доходу 25 домогосподарств (гр.од.) у ряд розподілу: Xi - 375;446;472;517;390;464;526;485;457;496;485;483; 412; 449;512;467;526;538;403;437; 504; 488; 454; 489; 472.
Першим кроком у побудові ряду розподілу є його ранжування, тобто розташування значень ознаки у зростаючому порядку: 375; 390; 403; 412; 437; 446; 449; 454; 457; 464; 467; 472; 472; 483; 485; 485; 488; 489; 496; 504; 512; 517; 526; 526; 538.
2. Ряд розподілу, побудований за кількісною ознакою, називається варіаційним. Побудуємо ряд розподілу, виражений у вигляді інтервалів. Такий ряд характеризує склад (структуру) досліджуваного явища, а також дозволяє судити про однорідність сукупності, закономірності розподілу і межах варіювання одиниць сукупності. Визначимо кількість груп, величину інтервалу, показники структури, кумулятивну чисельність, середину інтервалу. Кількість груп визначаємо за формулою Стерджеса: n = 1 + 3,322 lg N де N – число одиниць сукупності (=25). n = 1 + 3,322 lg25 = 5,6 або 5 (округлення відбувається до найближчого цілого). Результати розрахунку для деяких варіантів: N = 15 n = 4,9 приймаємо n = 5; N = 20 n = 5,3 приймаємо n = 5; N = 25 n = 5,6 приймаємо n = 6; N = 30 n = 5,9 приймаємо n = 6. Тоді розмір інтервалу можна визначити за формулою:
де n - кількість інтервалів; Х - значення варіюючої ознаки. Приймаємо розмір інтервалу 33. Округлення виконується до цілих, якщо у вихідних даних тільки цілі тризначні числа. В інших випадках округлення - до десятих (0,0). В результаті одержимо наступний інтервальний ряд розподілу грошового місячного доходу домогосподарств:
Як видно з даного ряду розподілу, більшість домогосподарств отримує місячний доход в межах 441 – 507 гр.од. Результати побудови ряду розподілу оформляються у вигляді таблиці. Таблиця 1.1. Розподіл доходу господарств
У нашому прикладі дані групуються за розміром доходу домогосподарств. Результативна ознака варіює як під впливом систематичного чинника, так і інших неврахованих випадкових чинників (внутрішньогрупова варіація). група 1: група 2: група 3: група 4: група 5:
Розрахуємо внутрішньогрупові дисперсії за формулою:
Внутрішньогрупові дисперсії показують варіації сум доходу в кожній групі, викликані всіма можливими чинниками. Розрахуємо середню з внутрішньогрупових дисперсій:
Середня з внутрішньогрупових дисперсій відображає варіацію суми доходу, обумовлену всіма чинниками, окрім розміру доходу, але в середньому по всій сукупності. Обчислимо міжгрупову дисперсію.
Міжгрупова дисперсія характеризує систематичну варіацію результативного порядку, обумовлену впливом ознаки - чинника, покладеного в підставу угрупування. Обчислимо загальну дисперсію, згідно правилу складання дисперсій, за наступною формулою:
Загальна дисперсія вимірює варіацію ознаки по всій сукупності під впливом всіх чинників, що зумовили цю варіацію. Чим більше частка міжгрупової дисперсії в загальній дисперсії, тим сильніше вплив группировочного ознаки. Для характеристики даного зв'язку застосовують емпіричний коефіцієнт детермінації:
У нашому прикладі:
Емпіричне кореляційне відношення:
Згідно якісній оцінці тісноти зв'язку Чеддока, в нашому прикладі існує дуже тісний зв'язок між сумою місячного доходу домогосподарства і розміром доходу як групувальної ознаки. Оформлення роботи
Розрахунково-графічна робота має бути написана на односторонніх аркушах білого папера формату А4 (210х297мм). Текст розрахунково-графічної роботи виконують: - машинописним способом – шрифтом Times New Roman або Times New Roman Cyr із розміром шрифта 14 пт через 1,5 інтервали; - рукописним. Відстань (поля) від краю листа до тексту не менш, мм: ліве – 25, праве, верхнє й нижнє – 15. Абзаци в тексті починаються відступом, рівним 1,25 мм. Вписувати в текстові документи, виготовлені машинописним способом, окремі слова, формули, умовні знаки (рукописним способом) слід чорними чорнилами або пастою, при виконанні ілюстрацій рекомендується використовувати різні кольори. Вписування тексту між рядків не допускається. Помилки, описки і графічні неточності, виявлені в процесі виконання документа, допускається виправляти акуратним підчищенням або зафарбовуванням «штрихом» і нанесенням на тому ж місці виправленого тексту (графіки) машинописним способом або рукописним способом - чорними чорнилом, пастою чи тушшю. Нумерація листів повинна бути наскрізною у правому нижньому куті. Першою сторінкою є титульний лист. На титульному листі роботи номер не ставлять. Формули та таблиці нумеруються наскрізною нумерацією арабськими цифрами в межах розділу. Номера формул записують на рівні формули праворуч у круглих дужках: (1.1), (1.2), і т.інш. СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ 1. Закон України "Про державну статистику" //Голос України. -2000. - 13 лип.; Відомості Верховної Ради України. - № 43. - К., 2000. 2. Бек В.Л. Теорія статистики: Навч. посібник. - К.: ТОВ „Центр учбової літератури", 2002. - 288с. 3. Гончарук А.Г. Основи статистики: Навч. посібник. - К.: ТОВ„Центр учбової літератури", 2004.-148 с. 4. Єріна А.М. Статистичне моделювання та прогнозування: Навч. посіб. - К.: КНЕУ, 2001. 5. Єріна А.М., Пальян З.О. Теорія статистики: Практикум. - К.: Знання, 2004. 6. Лугінін О.Є., Білоусова С.В. Статистика: Підручник. К.: Центр навч. літератури, 2005. – 580с. 7. Мармоза А. Т. Теорія статистики: Навч. посібник. - К.: Ельга, Ніка-Центр, 2003.-392 с. 8. Мармоза А.Т. Практикум з теорії статистики: Навч. посіб. - К.: Ніка-Центр, 2003. -344с. 9. Овчарук Р.Ю. Теорія статистики: Навч. посібник. - К.: Вікар,2003.-204 с. 10. Попов І.І., Федорченко В.С. Теорія статистики. Практикум: Навч. посіб. - К.: КНТЕУ. 2001. 11. Статистика: Навч.-метод. посібник для самост. вивч. дисц. / А.М.Єріна, Р.М.Моторін, А.В. Головач та ін. - К.: КНЕУ, 2002.-448с. 12. Статистика: Підручник / С.С.Герасименко А.В. Головач, А.М.Єріна та ін./ За наук. ред. С.С.Герасименка.- К.: КНЕУ, 2000.-460 с. 13. Теорія статистики: Навч. посіб. / П.Г.Вашків, П.І.Пастер,В.П.Сторожук, Є.І.Ткач. - К.: Либідь, 2001. – 320с. 14. Трінько Р. Теорія статистики: Навч. посіб. -Львів: Українські технології, 2003. 15. Уманець Т.В., Пігарєв Ю.Б. Статистика: Навч. посібник. - К.: Вікар, 2003.-623 с. 16. Уманець Т.В. Загальна теорія стастистики: Навч. посіб.-К.: Знання, 2006.-239 с. 17. Фінансова статистика: Навч. посібник /За кер. та наук. ред. В.Б.Захожая. - К.: МАУП, 2002. 18. Щурик М.В., Луцький І.М. Статистика: навч. посібник, Івано-Франківськ, 2004. 19. Щурик М.В. Статистика: Навч. пос. – Львів: «Магнолія-2006», 2009. – 545с. З м і с т вступ.. 4 1. Ряди розподілу.. 4 2. Характеристики центра розподілу.. 6 3. Статистичні характеристики варіації 8 4. Дослідження асиметрії розподілу.. 11 5. Приклад.. 16 6. оформлення роботи.. 29 СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ.. 30 Вступ
Методичні вказівки призначенідля практичного освоєння теоретичного курсу статистики з теми “Ряди розподілу” на конкретному прикладі в процесі виконання курсової роботи. Письмове виконання курсової роботи сприяє не тільки поглибленому вивчанню методів статистики, але й придбанню практичних навичок з розрахунку статистичних показників, правильної побудови й оформлення таблиць, графіків. Основна мета розробок – навчити розумінню суті розрахункових показників та їхнього аналізу. Керівник курсової роботи видає студентові завдання з вихідними даними, у т.ч. - на тему “Ряди розподілу”, і встановлює порядок, обсяг і термін завершення розрахунків, аналізу і підготовки до захисту. Керівник роботи: - контролює процес виконання роботи; - рекомендує літературу і довідкові матеріали; - проводить консультації зі студентами; - допомагає в обробці вихідних даних і в складанні висновків; - перевіряє виконані розрахунки. Перед рішенням кожної задачі необхідно ретельно вивчити її зміст. Перш ніж приступати до практичного виконання завдань, варто уважно ознайомитися із відповідним матеріалом методичних вказівок та літературою з рекомендованого списку.
Ряди розподілу
Ряд розподілу – це упорядкований розподіл одиниць сукупності на групи за певною ознакою, яка варіює. Залежно від статистичної природи варіантів ряди поділяються на атрибутивні та варіаційні. Варіаційний ряд розподілу – ряд, який будується за кількісною ознакою. При складанні структурних угруповань на основі кількісних варіюючих ознак необхідно визначити кількість груп та інтервали групування. Орієнтовно оптимальну кількість груп з рівними інтервалами можна визначити за формулою американського вченого Стерджесса: n=1+3,322 lgN, де N – число одиниць сукупності. Тоді величина інтервалу:
де xmax, xmin – найбільше і найменше значення ознаки; n – кількість груп. Після визначення ознаки групування та меж груп будується ряд розподілу. Ряд розподілу характеризує склад, структуру сукупності за визначеною ознакою. Варіаційні ряди розподілу складаються з двох елементів: варіант і частот. Числові значення кількісної ознаки у варіаційному ряді розподілу називаються варіантами. Частоти - це чисельність окремих варіант кожної групи варіаційного ряду, тобто це числа, що показують як часто зустрічаються ті чи інші варіанти в ряді розподілу. Сума всіх частот складає обсяг сукупності. Частки - це частоти, виражені у виді відносних одиниць (частках чи одиниць відсотків).
Варіаційні ряди в залежності від характеру варіації підрозділяються на дискретні та інтервальні. Дискретні засновані на дискретних (перервних) ознаках, що приймає тільки цілі значення; інтервальні - на безперервних ознаках (приймаючих будь-які значення). У співвідношенні варіантів і частот виявляється закономірність розподілу. Вона описується рядом статистичних характеристик, зокрема: а) частотні характеристики; б) характеристики центра розподілу; в) характеристики варіації; г)характеристики нерівномірності розподілу, концентрації, асиметрії.
Характеристики центра розподілу
Щоб визначити значення ознаки, характерне для всієї досліджуваної сукупності одиниць, виконують розрахунок середніх величин. Середньою величиною у статистиці називається узагальнюючий показник, що характеризує типовий рівень явища в конкретних умовах місця і часу, що відображає розмір варіюючої ознаки у розрахунку на одиницю якісно однорідної сукупності. В статистичній практиці в кожному конкретному випадку застосовується одна із середніх величин: арифметична, гармонійна, геометрична, квадратична, кубічна і т.д. Перераховані середні відносяться до класу статистичних середніх і поєднуються загальною формулою (при різних значеннях m):
де m – показник ступеню середньої; х – поточне значення (варіанта) ознаки, що усереднюється; n – кількість ознак. В залежності від значення показника ступеню m розрізняють наступні види статистичних середніх: при m = -1 – середня гармонійна при m = 0 – середня геометрична при m = 1 – середня арифметична при m = 2 – середня квадратична при m = 3 – середня кубічна
Кожна з даних середніх може приймати дві форми: просту і зважену. Якщо середня розраховується за первинними (незгрупованими) даними застосовується проста форма, якщо по вторинним (згрупованим) - застосовується зважена середня. Так, середня арифметична зважена обчислюється за формулою:
де
Структурні середні застосовуються для вивчення внутрішньої побудови і структури рядів розподілу. Мода (Мо) - це найбільш розповсюджене значення ознаки, тобто варіанта, що у ряді розподілу має найбільшу частоту (частку). В дискретному ряду Мо визначається візуально по максимальній частоті. В інтервальному ряді по найбільшій частоті визначається модальний інтервал.
де Хмо – нижня межа модального інтервалу; і – розмір інтервалу; fi, fi-1, fi+1 – частоти модального, передмодального і наступного за модальним інтервалів. Медіана (Ме) - це варіанта, що випадає на середину упорядкованого чи ранжованого ряду розподілу і поділяє його на дві рівні за обсягом частини. В дискретному ряду медіаною буде значення ознаки, для якого кумулятивна частота St перевищує половину обсягу сукупності, чи кумулятивна частина (частка) Sdj>=0,5. В інтервальному ряді в такий спосіб визначається медіанний інтервал.
де Хме - нижня межа медіанного інтервалу; і – розмір інтервалу; fi - частоти; fМе - частота медіанного інтервалу; Sме-1 – кумулятивна (накопичена) частота передмедіанного інтервалу.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.227.64 (0.012 с.) |
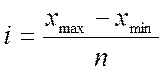 ,
,

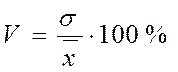


 =
= 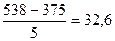 ,
, = 1168 / 3 = 389,3;
= 1168 / 3 = 389,3; = 849 / 2 = 424,5;
= 849 / 2 = 424,5; = 3681 / 8 = 460,1
= 3681 / 8 = 460,1 = 3430 / 7 = 490;
= 3430 / 7 = 490; = 2619 / 5 = 523,8;
= 2619 / 5 = 523,8; .
. 1 = ((375-389,3)2+(390-389,3)2+(403-389,3)2/3=392,67/3=130,89;
1 = ((375-389,3)2+(390-389,3)2+(403-389,3)2/3=392,67/3=130,89;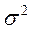 4 = ((483-490)2 + (485-490)2 + (485-490)2 + (488-490)2 + (489-490)2+ (496-490)2 + (504-490)2) = 336/7 = 48.
4 = ((483-490)2 + (485-490)2 + (485-490)2 + (488-490)2 + (489-490)2+ (496-490)2 + (504-490)2) = 336/7 = 48. .
. (130,89х3 + 156,25х2 + 91,26х8 + 48х7 + 79,36х5)/25 = 86,72.
(130,89х3 + 156,25х2 + 91,26х8 + 48х7 + 79,36х5)/25 = 86,72. .
. ((389,3-469,9)2 +(424,5-469,9)2 +(460,1-469,9)2 +(490-469,9)2 +(523,8-469,9)2) / 25 = 1669,35.
((389,3-469,9)2 +(424,5-469,9)2 +(460,1-469,9)2 +(490-469,9)2 +(523,8-469,9)2) / 25 = 1669,35. = 86,72 + 1669,35 = 1756,1.
= 86,72 + 1669,35 = 1756,1.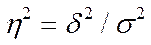 .
. 1669,35/1756,1=0,951.
1669,35/1756,1=0,951. .
. 0,975.
0,975.
 - середнє значення досліджуваного явища;
- середнє значення досліджуваного явища; ;
;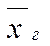 ;
;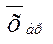 ;
; ;
; .
. ,
, - сума добутків величини ознак на їхні частоти;
- сума добутків величини ознак на їхні частоти; 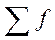 - загальна кількість одиниць сукупності.
- загальна кількість одиниць сукупності. ,
,