
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели в пространстве состоянийСодержание книги Поиск на нашем сайте
Для того, чтобы было легче исследовать модель объекта, желательно привести ее к неко-торому стандартному виду, для которого уже есть готовые общие решения. Таким «стандар-том» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.
Рассмотрим снова модель электродвигателя, считая, что M H (t) = 0 (нагрузки нет). Вспом-нив, что ω (t) = θ &(t), можно записать (12) в виде системы θ &(t)= ω (t)
ω &(t)= − kJ 1 kR 2⋅ ω (t)+ Jk 1 R ⋅ u (t)
Эта система дифференциальных уравнений первого порядка быть записана в матричной форме:
Значения θ (t) и ω (t) определяют состояние двигателя в момент времени t. Это значит, что зная их значения в некоторый момент времени t 0 и входной сигнал u (t) при всех t ≥ t 0
можно рассчитать поведение объекта для любого последующего момента. При этом предыду-щие значения θ (t), ω (t) и u (t) (при t < t 0) не играют никакой роли. Поэтому θ (t) и ω (t) назы- ваются переменными состояния, а вектор θ (t) – вектором состояния.
ω (t)
В теории управления принято обозначать вектор состояния через x (t), вход объекта (сиг-нал управления) – через u (t). Тогда модель (13) может быть записана в виде
где x (t)
стояния
x (t),поэтому она называется моделью вход-состояние.
© К.Ю. Поляков, 2008
Полная модель объекта в пространстве состояний содержит еще одно уравнение – уравне-ние выхода, которое показывает, как формируется выход объекта y (t): x &(t)= A ⋅ x (t)+ B ⋅ u (t) (15)
y (t)= C ⋅ x (t)+ D ⋅ u (t)
Эта модель называется моделью вход-состояние-выход. Выходная координата для двигателя постоянного тока – это угол поворота вала: y (t)= θ (t)=[1 0]⋅ θ (t)=[1 0]⋅ x (t), ω (t)
так что C = [1 0] и D = 0. Если же в качестве выхода принять угловую скорость, то C = [0 1].
С помощью модели (15), изменяя матрицы C и D, можно принять за выход любую ли-нейную комбинацию переменных состояния и входа. Во многих практических задачах выход – это одна или несколько переменных состояния, которые мы можем измерить.
Поскольку момент инерции J, сопротивление якоря R и коэффициенты k 1 и k 2 не зави-
сят от времени, матрицы A, B, C и D в модели (15) – постоянные. Такие объекты называются стационарными,в отличие от нестационарных объектов,параметры которых изменяются вовремени.
Запись моделей в единой форме (15) позволяет отвлечься от смысла переменных состоя-ния и исследовать системы разной природы стандартными методами, которые хорошо разрабо-таны и реализованы в современных компьютерных программах. Покажем, как уравнения вида (15) могут быть решены и чем удобна именно такая форма записи. Предположим, что мы знаем начальные условия, то есть вектор состояния x (0) при t =0.Вспомним,что знание x (0)и входа u (t)при всех t >0дает возможность однозначно оп-
ределить дальнейшее поведение этого объекта.
Первое уравнение в (15) позволяет найти производную, то есть, скорость изменения век-тора состояния x (t) в любой момент времени. Будем считать, что при 0 ≤ t ≤ ∆ t, где ∆ t – ма-
лый интервал времени, эта производная не меняется. Тогда значение вектора состояния при t = ∆ t приближенно определяется формулой
x (∆ t)≈ x (0)+ x &(0)⋅∆ t = x (0)+[ A ⋅ x (0)+ B ⋅ u (0)]⋅∆ t,
то есть, его можно легко вычислить. Зная x (∆ t) и сигнал управления u (∆ t), находим выход
системы в тот же момент
y (∆ t)≈ C ⋅ x (∆ t)+ D ⋅ u (∆ t).
Эту методику можно применять и дальше, в конце второго интервала получаем x (2⋅∆ t)≈ x (∆ t)+ x &(∆ t)⋅∆ t = x (∆ t)+[ A ⋅ x (∆ t)+ B ⋅ u (∆ t)]⋅∆ t,
y (2⋅∆ t)≈ C ⋅ x (2⋅∆ t)+ D ⋅ u (2⋅∆ t).
Таким образом, можно (приближенно) рассчитать выход системы при всех t > 0. Конечно, точ-ность будет тем выше, чем меньше ∆ t, однако объем вычислений при этом также увеличится. Этот метод приближенного решения дифференциальных уравнения называется методом Эйле-ра. Так как мы не делали никаких предположений о постоянных матрицах A, B, C и D,его(как и другие, более совершенные методы) можно использовать без изменений для решения любых уравнений вида (15).
Переходная функция
Один из методов построения моделей «вход-выход» – определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – так называемый «единичный скачок» («единичный ступенчатый сигнал»), то есть мгновенное изменение входного сигнала с 0 до 1 в момент t = 0. Формально этот сигнал определяется так:
0, t < 0 1 (t)=≥ 1, t 0
© К.Ю. Поляков, 2008
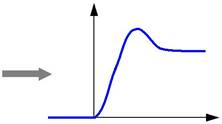
Реакция объекта на единичный скачок называется переходной функцией и обозначается h (t):
При этом предполагается, что объект в начальный момент находится в состоянии покоя, то есть, имеет нулевые начальные условия. Это значит, что все его переменные состояния равны нулю и внутренняя энергия также нулевая.
Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнения объекта или модель в пространстве состоя-ний. Это значит, что переходная характеристика дает меньше информации, чем исходные урав-нения.
Пусть модель объекта задана дифференциальным уравнением первого порядка:
где k – безразмерный коэффициент, а T – некоторая постоянная, которая имеет размерность времени (измеряется в секундах). Найдем переходную характеристику этого звена. Решая урав-нение (16) при x (t) =1 (t > 0), получаем
где постоянная C 1 должна определяться из начальных условий. Поскольку нас интересует пе-
y
k
T =1 c
Видно, что при увеличении T выход y медленнее достигает установившегося значения, равно-
го k, то есть постоянная времени характеризует инерционность звена (16). Чем больше посто-янная времени, чем медленнее реагирует объект на управление и тем больше усилий нужно для того, чтобы перевести его в новое состояние.
Заметим, что ступенчатый сигнал легко получить на практике, поэтому переходную ха-рактеристику можно снять экспериментально.
© К.Ю. Поляков, 2008
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.86.134 (0.011 с.) |






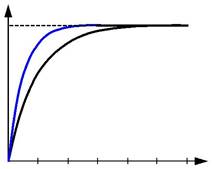 T =0,5 c
T =0,5 c


