
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые звенья САУ и их характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введение Теория автоматического управления является технической наукой общего применения. Она дает теоретическую базу для исследования, разработки и проектирования автоматических и автоматизированных систем. 1. Основные понятия и определения Существует чрезвычайно большое разнообразие систем, автоматически выполняющих те или иные функции по управлению различными физическими процессами во всех областях техники. Автоматическая система способна в течение длительного времени нужным образом изменять какие-либо физические величины в том или ином управляемом процессе. Автоматизированная система – система, в качестве одного из узлов которой используется человек-оператор. Операция управления – действия, направленные на правильное и высококачественное функционирование объекта управления. Они обеспечивают в нужный момент времени начало, порядок следования и прекращение отдельных действий; предусматривают выделение необходимых ресурсов и задают нужные параметры самому процессу. Объект управления – это совокупность технических средств, выполняющих определенный процесс и подлежащих управлению. Все системы автоматического управления (САУ) можно классифицировать следующим образом. 1. По виду структурной схемы: – разомкнутые (автоматы, работающие по некоторым программам); – замкнутые (с обратной связью). 2. По виду уравнений динамики процессов управления: – линейные; – нелинейные. Наиболее полно изучены линейные системы. 3. По характеру передачи сигнала: – непрерывные; – дискретные: – импульсные (дискретные по времени); – цифровые (дискретные по времени и по уровню); – релейные (сигнал изменяется скачком). 4. По характеру функционирования: – обычные; – адаптивные (самонастраивающиеся). 5. В зависимости от характера изменения управляющего воздействия: – системы автоматической стабилизации; – системы программного управления; – системы слежения. Типовая схема САУ выглядит следующим образом (рис. 1).
Рис. 1. Типовая схема САУ g (t) – задающее воздействие; f (t) – возмущающее воздействие (может действовать на любой блок системы); у (t) – выходной сигнал; 1 – задающее устройство. Устройство преобразует входное воздействие g (t) в сигнал, пропорциональный заданному значению выходной величины у (t); 2, 5 – устройства сравнения. Вырабатывают сигнал рассогласования (ошибки) е (t) между входным сигналом и сигналом главной обратной 3 – преобразующее устройство; 4, 8 – корректирующие устройства. Повышают качество управления; 6 – усилительное устройство; 7 – исполнительное устройство; 9 – измерительное устройство; 10 – согласующее устройство. Вырабатывает сигнал, находящийся в определенной функциональной зависимости от регулируемой переменной; 11 – объект управления. Таким образом, упрощенно любую САУ можно представить следующим образом (рис. 2).
Рис. 2. Упрощенная схема САУ Задачи теории САУ Теория автоматического управления изучает общие принципы построения САУ и методы их исследования независимо от физической природы процессов. Можно выделить две задачи. 1. Задача анализа: исследование статических и динамических свойств системы. 2. Задача синтеза: разработка новых систем, удовлетворяющих заданным техническим требованиям. При решении этих задач исследуются следующие вопросы. 1. Формирование функциональной и структурной схем САУ. 2. Построение статических и динамических характеристик отдельных звеньев и системы в целом. 3. Определение ошибок управления и показателей точности замкнутой системы. 4. Исследование устойчивости системы. 5. Оценка качественных показателей процесса управления. 6. Синтез корректирующих устройств и оптимизация параметров системы. 3. Дифференциальные уравнения и Для анализа систем необходимо иметь их математическое описание. Обычно это дифференциальные уравнения (ДУ). Если в этом уравнении используются производные входных и выходных величин, то это уравнение динамики. Если положить нулю производные входных сигналов, – это уравнение статики (описание системы в установившемся режиме). Эти уравнения составляются на основе физических законов. В общем случае полученные уравнения являются нелинейными. Для упрощения анализа применяют те или иные методы линеаризации, например, разложение в ряд Тейлора. В общем виде линейное дифференциальное уравнение имеет следующий вид:
В теории автоматического управления принята стандартная форма записи дифференциальных уравнений: Например, для уравнения второго порядка:
Параметр K называется коэффициентом передачи (коэффициент усиления). Это отношение выходной величины к входной в установившемся режиме. Параметр Т – постоянная времени. Такой вид представляет первую форму описания САУ. Кроме описания во временной области, системы описываются передаточными функциями. Чтобы получить передаточную функцию нужно использовать разложение Лапласа
где р = с + jd – комплексное число; f (t) – оригинал; F (p) – изображение по Лапласу. Соответственно и дифференциальное уравнение можно преобразовать и записать относительно изображений (см. пример выше):
Это вторая форма описания САУ. Передаточная функция – это отношение изображений выходной и входной величины, найденное из вышерассмотренного уравнения:
Для исследования частотных свойств САУ используется частотная передаточная функция. Для ее получения используется преобразование Фурье. При этом оператор p = j w, а частотная передаточная функция записывается в виде W (j w). Такое представление является третьей формой описания систем. Характеристики САУ Существуют различные методы исследования САУ или отдельных ее звеньев. Один из них заключается в анализе реакции системы или звена на внешнее воздействие. В качестве внешних воздействий используют стандартные сигналы. В теории САУ используют три вида сигнала. 1. Единичное входное воздействие 1(t) (рис. 3).
Рис. 3. Единичное входное воздействие 2. d-импульс – сигнал нулевой ширины и бесконечной амплитуды – d(t), причем его площадь равна 1 (рис. 4)
Рис. 4. Дельта-импульс Такая функция является математической абстракцией. Практически таким сигналом считается короткий импульс большой мощности. d-импульс математически связан с сигналом 1(t):
3. А sinw t, причем для простоты А = 1. Соответственно, на каждый из этих стандартных сигналов существует определенная реакция САУ. 1. Реакцией САУ или звена на единичное входное воздействие называется переходная характеристика или переходная функция h (t) (рис. 5).
Рис. 5. Пример переходной характеристики При использовании преобразования Лапласа получим
тогда изображение переходной характеристики
2. Реакцией системы на сигнал вида d(t) является весовая функция w(t) (рис. 6).
Рис. 6. Пример весовой функции САУ При использовании преобразования Лапласа получим следующие соотношения:
Преобразованием Лапласа от весовой функции является передаточная функция. Весовая функция и переходная характеристика связаны простым соотношением
Описание САУ во временной области через весовую функцию эквивалентно описанию передаточной функцией в области изображений. Можно найти реакцию системы на произвольный входной сигнал. Для этого можно воспользоваться интегралом Дюамеля или интегралом свертки
3. Если используется входной сигнал вида А sinw t, то говорят о частотных характеристиках системы. Частотные характеристики – это выражения и графические зависимости, выражающие реакцию исследуемой САУ на сигнал вида А sinw t при различных значениях частоты w. На выходе САУ сигнал будет иметь вид
где A (t) – амплитуда сигнала, j(t) – сдвиг фазы. Частотную передаточную функцию для получения частотных характеристик можно представить в следующем виде:
где u (w) и v (w) – действительная и мнимая части комплексного выражения. Вещественная часть состоит из четных степеней частоты w, а мнимая – из нечетных. Эту функцию можно представить графически на комплексной плоскости. Такое изображение называется годографом (рис. 7) или амплитудно-фазовой характеристикой. Кривая строится путем получения точек на плоскости при задании определенных значений частоты w и расчете u (w) и n(w). Для получения графика в случае отрицательных частот необходимо сделать зеркальное отображение имеющейся характеристики относительно действительной оси.
Рис. 7. Годограф или амплитудно-фазовая характеристика системы Аналогичным образом можно построить отдельно графики длины вектора А (w) и угла поворота j(w). Тогда получим амплитудно-частотную и фазо-частотную характеристики. На практике часто используют логарифмические характеристики. Логично использовать натуральный логарифм
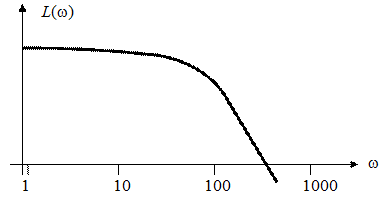
Однако на практике используют десятичные логарифмы и получают логарифмическую амплитудно-частотную (ЛАЧХ) (рис. 8) и логарифмическую фазо-частотную (ЛФЧХ) характеристики (рис. 9).
Рис. 8. Пример ЛАЧХ системы ЛАЧХ определяется по формуле
где | W (j w)| – модуль частотной передаточной функции. Единицей измерения является децибел.
Рис. 9. Пример ЛФЧХ системы При вычислении логарифмической фазочастотной характеристики используется (1). При построении графиков по оси абсцисс откладывают частоту в логарифмическом масштабе. Так как при вычислении значений ЛАЧХ в выражениях используются зависимости от степени w, то график имеет стандартный наклон, кратный 20 дБ/дек. Дек – декада, т. е. изменение частоты на порядок. Теоретически точка w = 0 на оси частот должна быть слева в бесконечности, но для практических расчетов ось ординат сдвигают вправо. Логарифмические характеристики имеют следующие достоинства: – простота построения; – легкость получения ЛАЧХ системы из ЛАЧХ звеньев путем геометрического сложения; – простота анализа САУ. Законы управления Это алгоритмы или функциональные зависимости, в соответствии с которыми формируется управляющее (регулирующее) воздействие. u (t) = F (x (t), g (t), f (t)), где x (t) – ошибка; g (t) – задающее воздействие; f (t) – возмущающее воздействие. Обычно: u (t) = F 1(x) + F 2(g) + F 3(f), где F 1(x) – управление по отклонению или ошибке; F 2(g) и F 3(f) – управление по соответствующему воздействию. Обычно рассматриваются линейные законы относительно Различают несколько типовых законов управления. 1. Пропорциональное управление.
В цепи управления находится пропорциональное (статическое) В установившемся режиме:
где K – общий коэффициент усиления системы; y УСТ – установившееся значение выходной величины; x 0 – постоянное значение ошибки. Для замкнутой САУ найдем установившееся значение ошибки по формуле (3):
где g 0 – постоянное входное воздействие; xf УСТ – установившаяся ошибка от возмущающего воздействия. Анализ выражения показывает, что установившаяся ошибка уменьшилась в (1 + K) раз, но в принципе не равна 0. 2. Интегральное управление. В этом случае имеет место зависимость между ошибкой и скоростью изменения регулирующего (управляющего) воздействия
В составе САУ обязательно имеются интегрирующие звенья. Установившееся значение ошибки находим по формуле (3). Первое слагаемое равно 0, второе зависит от значения числителя, поэтому для него применим выражение
При отсутствии возмущающего воздействия общее значение установившейся ошибки равно нулю. Система является астатической по задающему воздействию или обладает астатизмом первого порядка. Однако, если задающее воздействие переменно (скорость его изменения не равна 0), то установившаяся ошибка будет иметь ненулевое значение. Для устранения ошибки по скорости в САУ необходимо добавить еще один интегратор. Такой подход имеет недостаток: при наличии большого количества интеграторов процесс управления замедляется и изменяется устойчивость системы. 3. Управление по производной (дифференциальное). Процесс управления описывается соотношениями:
Процесс управления начинает действовать, когда ошибка еще равна 0, а ее производная отлична от 0. В установившемся режиме 4. Изодромное управление. Возможно использование всех вышеперечисленных законов одновременно. Закон управления в этом случае имеет вид:
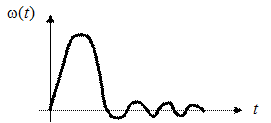
Такое управление сочетает достоинства всех рассмотренных законов. Например, при линейно изменяющемся входном воздействии (рис. 28) в начальный момент (участок I) действует управление по производной, затем больший вклад вносит пропорциональное управление, после момента времени t 0 (участок II) существенно интегральное управление.
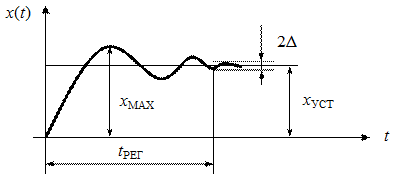
Рис. 28. Законы управления в САУ 9. Процесс управления и требования к нему Процесс управления во времени определяется решением дифференциального уравнения динамики замкнутой системы. При этом можно определить требования к системе по трем основным направлениям. 1. Принципиальная оценка возможности перехода системы в некоторое установившееся состояние при любом внешнем воздействии. Это оценка устойчивости системы. 2. Оценка качества переходного процесса. 3. Оценка точности системы в установившемся состоянии. Рассмотрим каждый из этих пунктов. Критерии устойчивости Критерии устойчивости можно разбить на две большие группы. 1. Алгебраические. 2. Частотные. Рассмотрим их подробнее. Показатели качества Требования к качеству процесса управления в каждом конкретном случае могут быть различными, но как правило, оценивается характер переходного процесса при единичном ступенчатом воздействии (рис. 40).
Рис. 40. Показатели качества переходного процесса Используются следующие показатели качества переходного 1. t РЕГ – время регулирования (длительность переходного процесса), время, в течение которого, начиная с момента приложения входного воздействия, отклонение выходной величины от ее установившегося значения, становится меньше наперед заданного значения ∆. Обычно выбирается ∆ = 5% от х УСТ. 2. Перерегулирование:
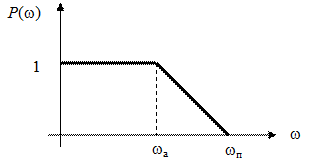
3. Колебательность – число полных колебаний выходной величины за время регулирования. 4. Установившаяся ошибка – это разность между задающим воздействием и установившимся значением выходной величины. Метод Солодовникова Здесь вводится понятие типовой единичной трапецеидальной вещественной характеристики. Ее высота равна 1, частота среза (частота положительности) wп =1 (рис. 41).
Рис. 41. Типовая единичная трапецеидальная вещественная характеристика Для данной трапеции существуют таблицы связи выходной величины х (t) от коэффициента наклона c = wа / wп. Метод заключается в выполнении следующей последовательности действий. 1. Строится график вещественной части частотной передаточной функции замкнутой системы. 2. График разбивается на трапеции. Эта процедура представлена на рис. 42. В данном примере получилось три типовые трапеции.
Рис. 42. Разбиение графика вещественной характеристики на трапеции 3. Для каждой трапеции по таблицам находятся значения выходного процесса x 1(t), x 2(t), x 3(t). 4. Находится результирующий график выходного сигнала путем сложения графиков x 1(t), x 2(t), x 3(t). Так как таблицы разработаны для единичной трапеции, то при построении переходного процесса для каждой трапеции, необходимо использовать правила (формулы) перехода к реальному значению отсчетов выходного сигнала. 1. Получение установившегося значения P (0) = x (∞) = x УСТ. 2. Получение действительной амплитуды сигнала
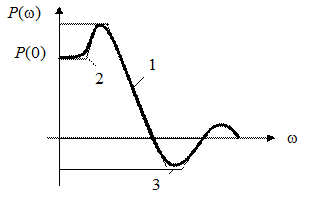
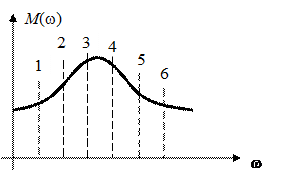
3. Изменение масштаба времени Показатели качества переходного процесса можно приближенно оценить по вещественной частотной характеристике замкнутой системы, не выполняя вышерассмотренных вычислений. Все разновидности графика этой характеристики представлены на рис. 43.
Рис. 43. Типовой вид графиков вещественной характеристики 1 – график характеристики имеет «горб»; 2 – «горба» нет, производная 3 – «горба» нет, В случае 1 переходный процесс х (t) имеет перерегулирование, причем его величина более 18%. В случае 2 переходный процесс х (t) имеет перерегулирование, причем его величина менее 18%. В случае 3 процесс управления монотонный. По графику можно приближенно определить и время переходного процесса
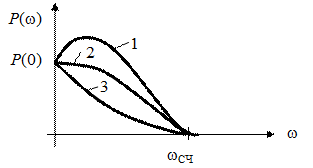
где wСЧ – диапазон существенных частот. Характеристика Р (w) в этом диапазоне превышает некоторый уровень e. Обычно e = 5%. Показатель колебательности Этот параметр используется для определения запаса устойчивости. Его можно вычислить по значению модуля частотной передаточной функции замкнутой системы
Показатель колебательности равен отношению
Рис. 44. Модуль частотной передаточной функции замкнутой системы Это относительная высота резонансного пика. Для упрощения расчетов считается, что М (0) = 1. При этом М К= М MAX. Физически показатель колебательности – это отношение максимальных значений выходного и входного сигналов САУ. Чем меньше запас устойчивости САУ, тем больше склонность системы к колебаниям, тем выше резонансный пик. Обычно показатель колебательности лежит в диапазоне 1,1 … 1,5. Mk можно определить по виду частотной характеристики разомкнутой системы, пользуясь передаточной функцией разомкнутой системы
Представив W (j w) через действительную U и мнимую V части, получим:
Данные соотношения описывают окружность, причем С – вещественная координата ее центра; R – радиус. На комплексной плоскости можно построить семейство окружностей с этими параметрами, зависящими от М. На этот график наносится годограф разомкнутой системы (рис. 45).
Рис. 45. Семейство окружностей для различных показателей колебательности На основе этого графика строится график модуля частотной характеристики. Находятся точки пересечения окружностей и годографа. Каждой такой точке соответствует значение модуля М (по окружностям) и значение частоты w (по годографу). Пара этих величин представляет координаты точки искомой характеристики (рис. 46).
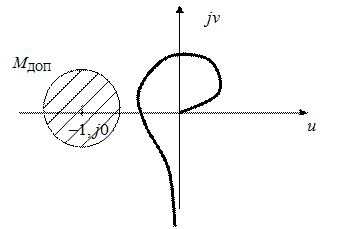
Рис. 46 Построение графика модуля частотной передаточной функции Иногда достаточно определить максимальное значение М MAX (по касанию АФХ соответствующей окружности). Возможно решение обратной задачи: задается допустимое значение показателя М ДОП. Необходимо соответствующим образом спроектировать систему. Для выполнения этого условия нужно обеспечить, чтобы годограф САУ не заходил в область, ограниченную окружностью с заданным значением М (рис. 47).
Рис. 47. Допустимая зона параметров САУ по показателю колебательности Синтез линейных САУ Способы синтеза САУ Главные цели проектирования САУ – обеспечение устойчивости системы и обеспечение требуемого качества переходного процесса. Достичь этих целей можно двумя способами. 1. Изменение параметров системы, т. е. изменение параметров звеньев (коэффициент усиления, постоянная времени). В ряде случаев такой подход не приводит к желаемому результату. 2. Изменение структуры системы. Обычно это введение дополнительных устройств или блоков (корректирующих устройств). Рассмотрим подробнее второй подход. В теории САУ различают 4 вида корректирующих устройств. 1. Последовательные корректирующие устройства (корректирующие фильтры). 2. Параллельные корректирующие устройства, обычно в виде местной обратной связи. 3. Корректирующие устройства по внешнему воздействию. 4. Неединичная главная обратная связь. Задание Необходимо выполнить следующие действия. 1. Описать работу системы. 2. Определить передаточные функции элементов системы. 3. Составить структурную схему системы. 4. Построить логарифмические характеристики разомкнутой 5. Определить устойчивость и запас устойчивости по амплитуде и фазе. 6. С помощью критерия Гурвица определить критическое значение добротности системы без обратной связи. 7. Ввести скоростную обратную связь. 8. Найти минимальное значение коэффициента скоростной обратной связи, необходимого для устойчивости системы. 9. Найти оптимальное значение коэффициента скоростной обратной связи, необходимого для обеспечения показателей качества переходного процесса системы. Исходная схема САУ (рис. 59):
Рис. 59. Исходная схема системы где СП – сельсинная пара; Р – редуктор; Д – двигатель; ОУ – объект управления; У – усилитель; КО – командная ось; ИО – исполнительная ось; α – угол поворота сельсин-датчика – это командное воздействие; β – угол поворота двигателя; γ – угол поворота редуктора – это исполнительное воздействие; U 1 – выходной сигнал СП; U 2 – выходной сигнал У; Параметры САУ: U MAX – максимальное напряжение на выходе сельсин-трансформатора; k У – коэффициент усиления У; T У – постоянная времени У; U У – номинальное напряжение на обмотке управления двигателя; N XX – число оборотов в минуту при холостом ходе двигателя и при номинальном напряжении двигателя; T Д – постоянная времени Д; i – передаточное число редуктора; S ТГ – крутизна выходной характеристики тахогенератора; t РЕГ – время регулирования; s – величина перерегулирования; n – число полных колебаний выходного сигнала. Исходные данные: k У = 900; T У = 0.01 с; T Д = 0.052 с; i = 1.2 × 103; U MAX = 5 В; U У = 30 В; N XX = 10000 об/мин; S ТГ = 0.001 В × с/рад; t РЕГ £ 1 с; s £ 30%; n = 1,5. Описание работы системы Из схемы системы, приведённой в задании видно (см. рис. 59), что задающим устройством является командная ось, вращаемая сельсин-датчиком по произвольному закону α = α(t). Тот же самый закон угла поворота во времени α(t) = γ(t) должен быть автоматически воспроизведён на выходе системы, т. е. на объект управления и на исполнительную ось. Если углы поворота командной и исполнительной оси не равны, (α(t) ¹ γ(t)), то на выходе сельсинной пары возникает напряжение рассогласования U 1. Величина U 1 зависит от величины углов поворота командной и исполнительной осей. Напряжение U 1 поступает на вход усилителя, на выходе которого возникает напряжение U 2, поступающее на обмотку управления двигателя. В результате этого начинает вращаться ротор двигателя в сторону уменьшения ошибки рассогласования (θ = α – γ) до согласования двух осей. То есть поворот ротора двигателя через редуктор задаёт новый закон угла поворота исполнительной оси. Ротор двигателя будет вращаться до тех пор, пока ошибка рассогласования не будет сведена к нулю, после чего он остановится. Таким образом, система охвачена отрицательной обратной связью. Случайные процессы в САУ Основные понятия Выше были изучены процессы работы САУ при поступлении на ее вход детерминированных сигналов. Во многих случаях входной сигнал может принимать случайные значения. При этом можно оценивать только вероятностные характеристики. Пример случайного воздействия: следящая система доплеровского измерителя скорости. Спектральные характеристики процессов САУ в этом случае представлены на рис. 66. Доплеровская частота W зависит не только от скорости движения объекта, но и от угла падения луча и вида подстилающей поверхности, поэтому носит случайный характер. При этом спектральная характеристика принимаемого сигнала имеет амплитуду S W и ширину Dw, изменяющуюся случайным образом.
Рис. 66. Спектральные характеристики случайных процессов САУ w0 – излучаемая частота; wП – принимаемая частота; Dw – ширина спектра. В этой следящей системе имеют место паразитные сигналы (шумы). В простейшем случае шум равномерно распространен по всем частотам.Его спектральная плотность N. Расчеты по минимуму ошибки Если на систему одновременно действует полезный сигнал и помеха, то может быть решена задача оптимального расчета системы с тем, чтобы обеспечить наименьшую результирующую ошибку системы. Критерием является минимальное значение результирующей ошибки системы, определяемой сигналом и помехой. Для случайных процессов обычно ограничиваются оценкой среднеквадратической ошибки. Необходимо обеспечить минимум среднеквадратической ошибки при одновременном действии сигнала и помехи. Критерий выглядит следующим образом:
Нежелательность ошибки пропорциональна квадрату ее величины. Возможны две формулировки данной задачи. 1. Имеется САУ заданной структуры. Необходимо так выбрать ее параметры, чтобы обеспечить минимум СКО при заданных статистических параметрах сигнала и ошибки. Решение ищется следующим образом: зная спектральную плотность ошибки, теоретически находится выражение для расчета дисперсии и СКО. Это выражение зависит от параметров системы, полезного сигнала и помехи. Ищутся условия на параметры системы для обеспечения минимума дисперсии. В простых случаях можно применить известные методы нахождения экстремума функции путем дифференцирования и приравнивания к нулю частных производных. 2. Ставится вопрос о нахождении оптимальной структуры системы и параметров звеньев для получения теоретически минимальной среднеквадратической ошибки при заданных вероятностных характеристиках полезного сигнала и помехи. Решение следующее: находится теоретическая передаточная функция замкнутой системы, и к ней стремятся при проектировании. Возможна ситуация, что реализация САУ с такой оптимальной передаточной функцией будет сопряжена со значительными трудностями. Нелинейные САУ Анализ нелинейных САУ (НСАУ) представляет собой достаточно трудную задачу. При ее решении стремятся свести такую САУ к линейной с определенными допущения и ограничениями. К таким системам относятся те, в которых имеется хотя бы одно звено, описываемое нелинейными дифференциальными уравнениями. Нелинейные звенья могут быть следующих видов: - релейного типа; - с кусочно-линейной характеристикой; - с криволинейной характеристикой любого очертания; - имеется произведение и другие комбинации переменных; - нелинейное звено с запаздыванием; - импульсное звено; - логическое; - описываемое кусочно-линейным дифференциальным уравнением. Нелинейности могут быть статические и динамические. Статические описываются нелинейными статическими характеристиками, а динамические – нелинейными дифференциальными уравнениями. Фазовое пространство Для наглядного представления процессов нелинейных САУ вводится понятие «фазовое пространство», которое заключается в следующем. Дифференциальное уравнение замкнутой системы n -го порядка заменяется системой дифференциальных уравнений первого порядка.
где x 1 – выходная величина; x 2 – xn – вспомогательные переменные; f, g – входные воздействия (возмущающее и задающее); x 10 = x 1(t = 0), x 20 = x 2(t = 0) … – начальные условия. Эти дифференциальные уравнения можно представить геометрически в n -мерном пространстве. Например, при n = 3 (рис. 75).
Рис. 75. Трехмерное фазовое пространство В реальном процессе управления в каждый момент времени величины x 1, x 2, x 3 имеют вполне определенные значения. Это соответствует вполне определенному положению точки М в пространстве. Точка М называется изображающей. С течением времени величины x 1, x 2, x 3 изменяются, точка М перемещается по определенной траектории, показывая так называемую фазовую траекторию. Следовательно, траектория движения точки М может служить наглядной геометрической иллюстрацией динамического поведения САУ в процессе управления. Рассмотрим пример фазовых траекторий некоторых линейных САУ. Пусть они описываются уравнением Рис. 76,а соответствует комплексным корням с отрицательной вещественной частью (наличие затухающего переходного процесса), случай рис. 76,б показывает фазовую траекторию апериодического затухающего процесса при отрицательных вещественных корнях характеристического уравнения. ДУ представляют собой выражения для проекций скорости изображающей точки М на óси координат. Поэтому по значениям правых частей уравнений в каждый момент времени можно судить о движении точки М, и, следовательно, о поведении реальной НСАУ в процессе управления. Фазовая траектория – это качественная характеристика НСАУ. Для определения количественных значений выходных сигналов необходимо решать дифференциальные уравнения в каждой точке. Если дифференциальные уравнения составлены для отклонений выходного сигнала от установившихся значений, то для устойчивой системы фазовая кривая будет стремиться в начало координат.
б) Рис. 76. Примеры фазовых траекторий Устойчивость по Ляпунову Для нели
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 5216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.10.127 (0.017 с.) |


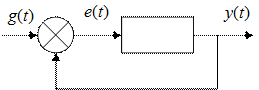
 .
.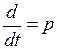 – производная заменяется на оператор p, коэффициент при выходной величине должен быть равен 1.
– производная заменяется на оператор p, коэффициент при выходной величине должен быть равен 1.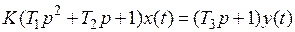 .
.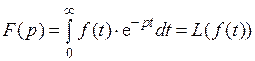 ,
,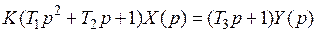 .
. .
.

 .
.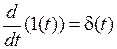 .
.
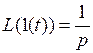 ,
, .
.
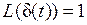 ;
;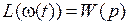 .
.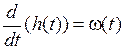 .
.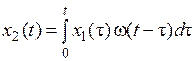 .
. ,
,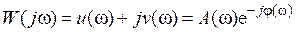 ;
;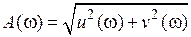 ;
;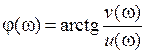 , (1)
, (1)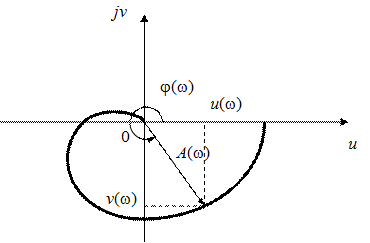
 .
.
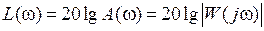 ,
,
 в ДУ.
в ДУ. ;
; .
. ,
, ,
, ;
; .
. .
. ;
; .
. и цепь управления разрывается, следовательно, данный закон не имеет самостоятельного значения. Используется как дополнение к другим. Он обеспечивает быструю реакцию САУ в переходном режиме.
и цепь управления разрывается, следовательно, данный закон не имеет самостоятельного значения. Используется как дополнение к другим. Он обеспечивает быструю реакцию САУ в переходном режиме. .
.
 .
.
 .
.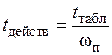 .
.
 и принимает различные значения;
и принимает различные значения; ,
, .
.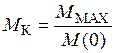 и представлен на рис. 44.
и представлен на рис. 44.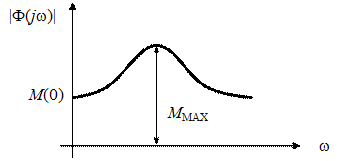
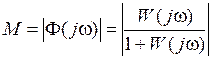 .
.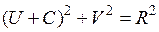 ;
;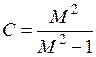 ;
;
 .
.


 .
.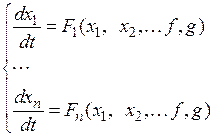 ,
,
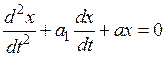 . В зависимости от параметров ДУ возможно несколько случаев. Некоторые из них представлены на рис. 76.
. В зависимости от параметров ДУ возможно несколько случаев. Некоторые из них представлены на рис. 76.
 а)
а)


