
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введение скоростной обратной связиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для того чтобы исходную систему (см. задание) сделать устойчивой, необходимо дополнительно ввести местную отрицательную обратную связь. Воспользуемся скоростной обратной связью. Для введения скоростной обратной связи в систему включается дифференцирующее звено – тахогенератор (ТГ) согласно рис. 62.
Рис. 62. Схема системы со скоростной обратной связью Важным свойством скоростной обратной связи является способность уменьшать постоянные времени тех звеньев, которые она охватывает. Данная скоростная ОС охватывает 2 звена: усилитель и двигатель. Перейдем к структурной схеме. Для этого найдем сначала передаточную функцию цепи скоростной обратной связи, т. е. передаточную функцию тахогенератора. Так как тахогенератор – это дифференцирующее звено, то передаточная функция имеет вид:
где
Структурная схема системы с отрицательной обратной связью будет иметь вид, приведенный на рис. 63.
Рис. 63. Структурная схема системы с ОС 11.9. Нахождение минимального коэффициента Для определения минимального коэффициента воспользуемся критерием устойчивости Гурвица. Но для этого сначала найдем результирующую передаточную функцию системы, представленной на рис. 63, и ее характеристическое уравнение. Эту передаточную функцию будем находить путем замены нескольких звеньев одним звеном с результирующей передаточной функцией для этих звеньев. Заменим блоки 2 и 3 на блок 2-3 с передаточной функцией: В результате замены получится следующая структурная схема (рис. 64).
Рис. 64. Структурная схема системы с ОС после 1-го преобразования Далее заменим блоки 2 – 3 и 5 одним блоком 2 – 3 – 5 с передаточной функцией:
т. к. блок 5 выполнен в виде обратной связи. В результате этой замены получим схему (рис. 65):
Рис. 65. Структурная схема системы с ОС после 2-го преобразования Из этой схемы видно, что система состоит из трех последовательно соединенных звеньев, следовательно,
Подставив выражения передаточных функций в эту формулу, получим:
Далее находим характеристическое уравнение системы с передаточной функцией (8) по формуле (7). Полученное уравнение будет иметь вид:
Заменим коэффициенты в этом уравнении
Исходя из этого уравнения третьего порядка, определяем критерий устойчивости Гурвица. По критерию Гурвица система будет устойчива, если будут выполняться следующие условия:
Из последнего условия и определяем минимальный коэффициент скоростной обратной связи
Подставив значения переменных, получим: 11.10 Определение оптимального коэффициента Это коэффициент, обеспечивающий требуемые показатели качества переходного процесса. Воспользуемся корневым методом. Он позволяет учесть эти показатели качества, не исследуя сам переходный процесс, а накладывая ограничения на корни характеристического уравнения. В примере уравнение третьего порядка. Его можно представить в
где р 1, р 2, р 3 – корни характеристического уравнения. Согласно методу, система склонна к колебаниям, если корни комплексные, т. е. Коэффициенты α и β через показатели качества высчитываются следующим образом:
где e – степень устойчивости; ∆ = 0,05; x – затухание за один период. Обычно лежит в диапазоне 0,90…0,98; m = 1,5 – колебательность; Т 0 = Т РЕГ = 1 с – длительность переходного процесса. В результате получим
Корень р 3 найдем из следующих соображений: берем исходное уравнение и приравниваем все коэффициенты при переменных одной степени.
Оптимальный коэффициент усиления тахогенератора находится из следующего соотношения:
Получаем:
Этот коэффициент больше минимального, рассчитанного выше, поэтому требования устойчивости соблюдаются. Случайные процессы в САУ Основные понятия Выше были изучены процессы работы САУ при поступлении на ее вход детерминированных сигналов. Во многих случаях входной сигнал может принимать случайные значения. При этом можно оценивать только вероятностные характеристики. Пример случайного воздействия: следящая система доплеровского измерителя скорости. Спектральные характеристики процессов САУ в этом случае представлены на рис. 66.
Доплеровская частота W зависит не только от скорости движения объекта, но и от угла падения луча и вида подстилающей поверхности, поэтому носит случайный характер. При этом спектральная характеристика принимаемого сигнала имеет амплитуду S W и ширину Dw, изменяющуюся случайным образом.
Рис. 66. Спектральные характеристики случайных процессов САУ w0 – излучаемая частота; wП – принимаемая частота; Dw – ширина спектра. В этой следящей системе имеют место паразитные сигналы (шумы). В простейшем случае шум равномерно распространен по всем частотам.Его спектральная плотность N.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.20.34 (0.009 с.) |


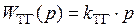 ,
, – коэффициент передачи тахогенератора.
– коэффициент передачи тахогенератора.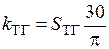 ;
; .
.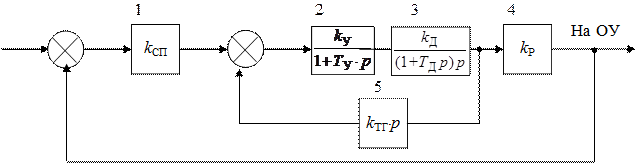
 , т. к. блоки 2 и 3 соединены последовательно.
, т. к. блоки 2 и 3 соединены последовательно.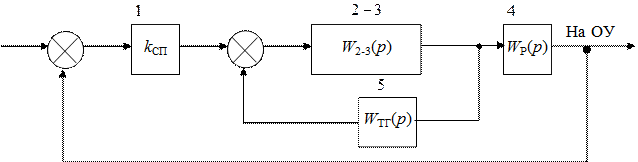
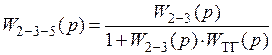 ,
,
 будет определяться следующим
будет определяться следующим 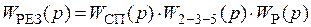
 . (8)
. (8) .
. .
. ,
,  .
.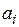 и выделив
и выделив 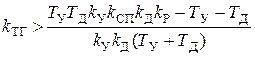 .
. , следовательно
, следовательно  .
.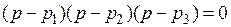 ,
, . Корень р 3 найдем через р 1 и р 2.
. Корень р 3 найдем через р 1 и р 2.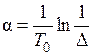 ;
; ,
,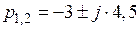 .
. , следовательно, р 3 = –8570.
, следовательно, р 3 = –8570. .
. .
.



