
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение структурной схемы системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При построении структурной схемы системы, приведенной в задании, воспользуемся передаточными функциями элементов, которые были получены выше. Полученная структурная схема системы изображена на рис. 60.
Рис.60. Структурная схема системы 11.5. Построение логарифмических частотных Для построения логарифмических частотных характеристик необходимо найти передаточную функцию всей системы. Так как данная система состоит из включенных последовательно звеньев, то передаточная функция разомкнутой системы будет равна произведению передаточных функций отдельных звеньев:
где k – общий коэффициент усиления разомкнутой цепи. В выражении (4) параметры k,
1. Логарифмическая амплитудно-частотная характеристика ЛАЧХ следящей системы с передаточной функцией (4) имеет следующий вид:
Учитывая, что наибольшей постоянной времени соответствует наименьшее значение частоты, определяем сопрягающие частоты, начиная с меньшей:
Переходя к декадам, получаем:
Наносим сопрягающие частоты на график (рис. 61). Находим точку Учитывая, что v =1 (где v – число, указывающее на порядок астатизма системы), т. к. в знаменателе равенства (4) стоит p, проводим низкочастотную асимптоту с наклоном
Рис. 61. ЛАЧХ и ЛФЧХ системы без обратной связи Так как постоянная Постоянная времени Полученная ЛАЧХ изображена на рис. 61 (верхний график). 2. Логарифмическая фазочастотная характеристика. Формула ЛФЧХ следящей системы с передаточной функцией (4) имеет следующий вид:
Это выражение позволяет построить – по точкам; – как сумму ординат ЛФЧХ двух апериодических звеньев с постоянными времени Построим ЛФЧХ по точкам. Наносим сопрягающие частоты
Таблица 2 Значения ЛФЧХ
Полученная ЛФЧХ изображена на рис. 61 (нижний график). 11.6. Определение устойчивости и запаса По графикам, приведенным на рис. 61, видно, что данная следящая система неустойчивая, т. к. ЛФЧХ пересекает прямую Следовательно, для данной системы запаса устойчивости по амплитуде и фазе нет. 11.7. Определение критического значения добротности Для определения критического значения добротности с помощью критерия Гурвица необходимо составить характеристическое уравнение системы. Для этого представим передаточную функцию (4) в виде отношения двух полиномов:
где k – общий коэффициент усиления разомкнутой системы, который часто называют добротностью системы;
При этом степень полинома в знаменателе больше, чем степень полинома в числителе. Полиномы в выражении (5) имеют вид:
где коэффициенты
Далее запишем характеристический полином для выражения (5):
Приравняв его к нулю, получим характеристическое уравнение системы с передаточной функцией (4):
Это выражение можно записать и в более удобной форме:
Подставив значения полиномов в выражение (6), получим следующее характеристическое уравнение вида:
Критическое значение добротности Из последнего условия и определим
Подставив выражения коэффициентов
Определив
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |




 , (4)
, (4)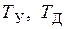 имеют следующие числовые
имеют следующие числовые 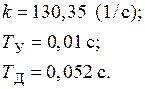
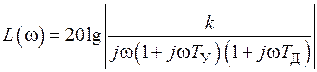 ;
; ;
; .
.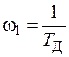 ,
,  ;
; ,
, 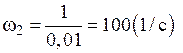 .
. ;
; .
.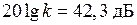 и наносим её на верхний график.
и наносим её на верхний график. до точки, соответствующей
до точки, соответствующей 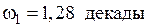 , с таким расчётом, чтобы эта асимптота пересекала ось ординат в точке 42,3 дБ.
, с таким расчётом, чтобы эта асимптота пересекала ось ординат в точке 42,3 дБ.
 , определяющая частоту w1, стоит в знаменателе передаточной функции (4), то увеличиваем наклон следующего участка характеристики на 20 дБ/дек (отклоняем характеристику вниз) и проводим его с наклоном –40 дБ/дек до точки, соответствующей w1 = 2 декадам.
, определяющая частоту w1, стоит в знаменателе передаточной функции (4), то увеличиваем наклон следующего участка характеристики на 20 дБ/дек (отклоняем характеристику вниз) и проводим его с наклоном –40 дБ/дек до точки, соответствующей w1 = 2 декадам. , определяющая частоту w2, стоит в знаменателе выражения (4), поэтому наклон следующего участка увеличиваем на 20 дБ/дек и проводим её последний участок с наклоном –60 дБ/дек
, определяющая частоту w2, стоит в знаменателе выражения (4), поэтому наклон следующего участка увеличиваем на 20 дБ/дек и проводим её последний участок с наклоном –60 дБ/дек .
. двумя способами:
двумя способами: и интегрирующего звена.
и интегрирующего звена.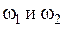 , рассчитанные для ЛАЧХ, на график (см. рис. 61). Далее строим ЛФЧХ по значениям, приведенным в табл. 2.
, рассчитанные для ЛАЧХ, на график (см. рис. 61). Далее строим ЛФЧХ по значениям, приведенным в табл. 2.
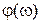
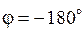 в пределах положительной ЛАЧХ.
в пределах положительной ЛАЧХ.
 , (5)
, (5) – полином числителя;
– полином числителя; – полином знаменателя.
– полином знаменателя.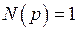 ;
; ,
,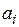 имеют следующие выражения:
имеют следующие выражения:
 .
. (6)
(6) (7)
(7)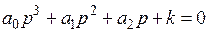 .
. определим из критерия устойчивости Гурвица. Для уравнения 3-го порядка критерий устойчивости имеет следующие условия:
определим из критерия устойчивости Гурвица. Для уравнения 3-го порядка критерий устойчивости имеет следующие условия:  .
. :
: .
. , получим, что
, получим, что ;
;
 , подтвердили, что наша система неустойчива, т. к.
, подтвердили, что наша система неустойчива, т. к. 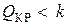 . Для того, чтобы система была устойчива, необходимо выполнение условия:
. Для того, чтобы система была устойчива, необходимо выполнение условия: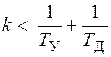 .
.


