Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики случайных величин и процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Кратко остановимся на основных характеристиках случайных величин и процессов. Случайная величина может быть непрерывной и дискретной. Случайным процессом называется изменение случайной величины во времени. Важное значение при описании случайных величин и процессов имеет понятие вероятности. Вероятность – это предельное значение частоты появления события
где n – число появлений события в испытаниях; N – общее число испытаний. Полное описание случайной величины дает закон распределения вероятности P (х) для дискретной величины и закон распределения плотности вероятности W (х) для непрерывной величины. Соотношение между этими параметрами представлено на рис. 67. Часто при анализе случайных величин и процессов ограничиваются частными характеристиками. Как правило, это математическое ожидание
Рис. 67. Плотность вероятности и вероятность для непрерывной величины Математическое ожидание можно определить как среднее значение, а дисперсию – как средний разброс значений случайной величины относительно ее математического ожидания. Для непрерывной величины справедливы выражения
Важное значение в теории случайных процессов имеет понятие корреляционной функции R. Она показывает степень влияния друг на друга или двух случайных процессов, или различных значений одного случайного процесса. В последнем случае для моментов времени t 1 и t 2 имеем
где W 2 – это двумерная плотность распределения вероятности для процессов x 1 и x 2. Существует широкий класс стационарных случайных процессов. У этих процессов постоянные вероятностные параметры. Поэтому корреляционная функция в данном случае будет зависеть только от расстояния между отсчетами t = t 1 – t 2,. Она обычно обозначается как R (t). Свойства корреляционной функции (рис. 68): 1) четная R (–t) = R (t); 2) убывающая; 3) если t = 0, то R (t) = D (дисперсия). В теории случайных процессов широко используется понятие спектральной плотности. Существует простая связь между спектральной плотностью и корреляционной функцией через преобразование Фурье:
Рис. 68. Корреляционная функция Если корреляционная функция и спектральная плотность – вещественные четные функции, то
Чем шире спектр случайного сигнала (сигнал быстрее изменяется), тем ýже корреляционная функция (слабее влияние соседних значений сигнала друг на друга) и наоборот. Предельное соотношение для сигнала типа шум – соседние значения сигнала не зависят друг от друга. 12.3. Прохождение случайного сигнала Структурная схема САУ имеет вид (рис. 69).
Рис. 69. Структура САУ Задачу можно сформулировать следующим образом: зная вероятностные характеристики входного сигнала x 1(t) (матожидание Существует два метода решения этой задачи: 1) расчеты во временной области; 2) расчеты в частотной области. 1. Расчеты во временной области. Рассмотрим математические соотношения для каждого метода. Для определения математического ожидания используется формула свертки, в которую вместо значений сигналов нужно подставить значения их математических ожиданий.
где w(t) – весовая функция. Для нахождения дисперсии на выходе предварительно необходимо найти корреляционную функцию. Корреляционная функция на выходе:
где h и l – переменные интегрирования При подстановке t = t 1 получим выражение для дисперсии. Если САУ устойчива, то корреляционная функция и дисперсия стремятся к некоторым пределам, определяющим стационарный процесс на выходе. Рассмотрим пример. Имеется интегрирующее звено с передаточной функцией На вход подается белый гауссовский шум (БГШ) с характеристиками (рис. 70). «Белый» шум означает равномерное распределение спектральной плотности N Ш во всем диапазоне частот. «Гауссовский» – плотность распределения вероятности имеет нормальный закон. Корреляционная функция шума В результате матожидание на выходе
а) б) Рис. 70. Характеристики БГШ
Анализ последнего выражения показывает, что дисперсия на выходе растет пропорционально времени и стремится к бесконечности. Это легко объяснить, если вспомнить, что данное звено является неустойчивым. 2. Расчеты в частотной области. Более удобно для расчета параметров случайного сигнала на выходе пользоваться спектральными характеристиками. Спектральную плотность на входе и выходе САУ можно определить через изображение Фурье входного S 1(w) и выходного S 2(w) сигналов
С другой стороны, для линейной САУ известно соотношение через частотную передаточную функцию:
Отсюда:
Строго говоря, такой подход справедлив, если закон распределения случайной величины при прохождении через систему не меняется. Это выполняется в случае нормального закона распределения случайной величины. Плотность распределения вероятности этого закона
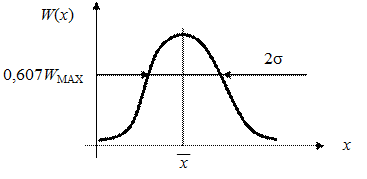
где s – среднеквадратичное отклонение, а график представлен на рис. 71.
Рис. 71. Нормальный закон распределения случайной величины
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 599; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 ,
, и дисперсия D.
и дисперсия D.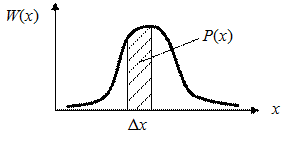
 – математическое ожидание;
– математическое ожидание; – дисперсия.
– дисперсия. ,
,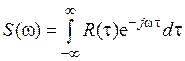 ;
;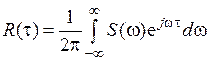 .
.
 ;
; .
.
 и дисперсию D 1), надо определить вероятностные характеристики выходного сигнала x 2(t) (матожидание
и дисперсию D 1), надо определить вероятностные характеристики выходного сигнала x 2(t) (матожидание 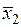 и дисперсию D 2).
и дисперсию D 2). ,
,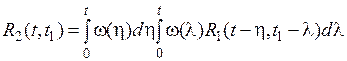 ,
,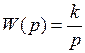 и весовой функцией
и весовой функцией  ;
;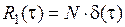 , матожидание шума
, матожидание шума  .
. , а дисперсия
, а дисперсия .
.
 ;
; .
. .
. ;
;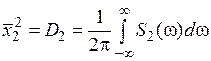 .
. ,
,