
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение передаточных функций САУСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Анализ САУ с помощью передаточных функций начинается с построения структурной схемы. Структурная схема – это изображение звеньев со связями между ними. Для звеньев указываются их передаточные функции. В теории САУ существует три вида соединения звеньев. 1. Последовательное.
Рис. 22. Последовательное соединение звеньев САУ Если при соединении звеньев не изменяется ДУ каждого звена, то эквивалентная передаточная функция равна W Э(p) = W 1(p)× W 2(p). 2. Параллельное. Структурная схема такого соединения имеет вид (рис. 23). W Э(p) = W 1(p) + W 2(p).
Рис 23. Параллельное соединение звеньев САУ 3. Обратная связь. Такое соединение имеет следующую структурную схему (рис. 24).
Рис. 24. Соединение в виде обратной связи Получить выражение для W Э(p) можно из следующих соотношений: e (t) = g (t) ± z (t); z (t) = y (t) × W 2(p); y (t) = e (t) × W 1(p);
Получим Существуют определенные правила преобразования структурных схем. Основное условие заключается в том, чтобы обеспечить неизменность действия сигналов в эквивалентных точках структурной схемы. 1. Перенос сумматора (рис. 25). 2. Перенос узла (рис. 26).
Рис. 25. Перенос сумматора в структурной схеме САУ
Рис. 26. Перенос узла в структурной схеме САУ 7. Составление исходных дифференциальных Как уже отмечалось выше, ДУ получаются на основании физической природы объекта. Затем при необходимости производится их линеаризация. При этом к системе могут быть приложены некоторые воздействия: 1) задающее воздействие g (t), которое определяет требуемый закон изменения выходной величины; 2) возмущающее воздействие f (t). Если действуют несколько входных сигналов, то используется принцип суперпозиции. ДУ можно составить как относительно выходной регулируемой величины, так и относительно сигнала ошибки x (t). Дифференциальное уравнение относительно ошибки в общем виде имеет следующий вид.
где D (p), Q (p), P (p) – полиномы, причем D называется характеристическим полиномом.
Структурная схема САУ при этом имеет следующий вид (рис. 27), сопоставимый с видом САУ, описанным в разделе Основные понятия и определения (см. рис. 1).
Рис. 27. Структура САУ ПУ – преобразующее устройство; ИЭ – исполнительный элемент; РО – регулируемый объект; u (t) – регулирующее (управляющее) воздействие. Рассмотрим первоначально разомкнутую (без обратной связи) САУ. Математические соотношения при этом имеют вид:
где W 0(р) – передаточная функция по регулирующему воздействию u (t); Wf (р) – передаточная функция по возмущающему воздействию. В теории САУ широко используется понятие передаточной функции разомкнутой системы:
Рассмотрим замкнутую систему. Для этого нужно использовать уравнение замыкания (2). Выражение для выходного сигнала в этом случае будет иметь вид:
а для ошибки САУ:
Анализ двух последних выражений позволяет определить следующие виды передаточных функций замкнутой САУ: 1) 2) Эти функции можно представить и через изображения сигналов, поступающих и проходящих через САУ Передаточную функцию разомкнутой системы можно представить в виде дробно-рациональной функции. Характеристический полином D (p) может быть найден как знаменатель передаточной функции замкнутой системы 1 + W (p). Важное значение в теории САУ имеет характеристическое D (p) = 0; 1 + W (p) = 0. Законы управления Это алгоритмы или функциональные зависимости, в соответствии с которыми формируется управляющее (регулирующее) воздействие. u (t) = F (x (t), g (t), f (t)), где x (t) – ошибка; g (t) – задающее воздействие; f (t) – возмущающее воздействие. Обычно: u (t) = F 1(x) + F 2(g) + F 3(f), где F 1(x) – управление по отклонению или ошибке; F 2(g) и F 3(f) – управление по соответствующему воздействию. Обычно рассматриваются линейные законы относительно Различают несколько типовых законов управления. 1. Пропорциональное управление.
В цепи управления находится пропорциональное (статическое) В установившемся режиме:
где K – общий коэффициент усиления системы; y УСТ – установившееся значение выходной величины; x 0 – постоянное значение ошибки. Для замкнутой САУ найдем установившееся значение ошибки по формуле (3):
где g 0 – постоянное входное воздействие; xf УСТ – установившаяся ошибка от возмущающего воздействия. Анализ выражения показывает, что установившаяся ошибка уменьшилась в (1 + K) раз, но в принципе не равна 0. 2. Интегральное управление. В этом случае имеет место зависимость между ошибкой и скоростью изменения регулирующего (управляющего) воздействия
В составе САУ обязательно имеются интегрирующие звенья. Установившееся значение ошибки находим по формуле (3). Первое слагаемое равно 0, второе зависит от значения числителя, поэтому для него применим выражение
При отсутствии возмущающего воздействия общее значение установившейся ошибки равно нулю. Система является астатической по задающему воздействию или обладает астатизмом первого порядка. Однако, если задающее воздействие переменно (скорость его изменения не равна 0), то установившаяся ошибка будет иметь ненулевое значение. Для устранения ошибки по скорости в САУ необходимо добавить еще один интегратор. Такой подход имеет недостаток: при наличии большого количества интеграторов процесс управления замедляется и изменяется устойчивость системы. 3. Управление по производной (дифференциальное). Процесс управления описывается соотношениями:
Процесс управления начинает действовать, когда ошибка еще равна 0, а ее производная отлична от 0. В установившемся режиме 4. Изодромное управление. Возможно использование всех вышеперечисленных законов одновременно. Закон управления в этом случае имеет вид:
Такое управление сочетает достоинства всех рассмотренных законов. Например, при линейно изменяющемся входном воздействии (рис. 28) в начальный момент (участок I) действует управление по производной, затем больший вклад вносит пропорциональное управление, после момента времени t 0 (участок II) существенно интегральное управление.
Рис. 28. Законы управления в САУ 9. Процесс управления и требования к нему Процесс управления во времени определяется решением дифференциального уравнения динамики замкнутой системы. При этом можно определить требования к системе по трем основным направлениям. 1. Принципиальная оценка возможности перехода системы в некоторое установившееся состояние при любом внешнем воздействии. Это оценка устойчивости системы. 2. Оценка качества переходного процесса. 3. Оценка точности системы в установившемся состоянии. Рассмотрим каждый из этих пунктов.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 Структурная схема такого соединения представлена на рис. 22.
Структурная схема такого соединения представлена на рис. 22.

 .
. .
.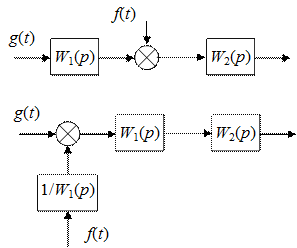

 ,
, ;
; . (2)
. (2)
 ;
; ,
, ;
; .
. ,
, , (3)
, (3) – передаточная функция замкнутой системы;
– передаточная функция замкнутой системы; – передаточная функция замкнутой системы по ошибке.
– передаточная функция замкнутой системы по ошибке. ,
,  .
. в ДУ.
в ДУ. ;
; .
. ,
, ,
, ;
; .
. .
. ;
; .
. и цепь управления разрывается, следовательно, данный закон не имеет самостоятельного значения. Используется как дополнение к другим. Он обеспечивает быструю реакцию САУ в переходном режиме.
и цепь управления разрывается, следовательно, данный закон не имеет самостоятельного значения. Используется как дополнение к другим. Он обеспечивает быструю реакцию САУ в переходном режиме. .
.



