
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Понятие передаточной функции и частотныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Характеристик системы 5.1. Элементы операционного исчисления. Преобразование Лапласа Под операционным исчислением понимается совокупность методов прикладного математического анализа, позволяющих экономными и непосредственно ведущими к цели средствами получать решения линейных дифференциальных уравнений. Операционное исчисление нашло широкое применение в теории автоматического управления, где с его помощью производится анализ переходных и установившихся процессов в автоматических системах. Понятие оператора является обобщением понятия функции. Функция – закон соответствия между двумя множествами чисел. Оператор – это закон соответствия между двумя множествами функций. Этот закон может быть задан, например, таблицей, где каждой функции f (t) из определенного класса соответствует какая–либо иная функция F (p). Закон соответствия может быть записан следующим образом: f (t) ® F (p). (Стрелка означает «соответствует»). В операционном исчислении рассматриваются операторы, заданные некоторой частной формулой преобразования. Так, пусть задана некоторая функция f (t) действительной переменной t, причем такая, что для нее существует преобразование Лапласа (L –преобразование)
Используя L –преобразование, можно каждой преобразуемой по Лапласу функции f (t) (в этом случае функция f (t) называется «оригиналом») поставить в соответствие функцию F (p) комплексной переменной р = с + j w (при этом функция F (p) называется «изображением» функции f (t)). Преобразование Лапласа обладает рядом замечательных свойств. Например, дифференцированию оригинала f (t) по переменной t соответствует операция умножения изображения F (p) на комплексную переменную р, а интегрированию оригинала f (t) соответствует операция деления F (p) на р. Таком образом, операции дифференцирования и интегрирования оригинала заменяются в пространстве изображений оригинала более простыми операциями алгебры – соответственно умножением и делением изображения F (p) на р. Это позволяет дифференциальное уравнение, записанное относительно искомой функции f (t), заменить в пространстве изображений на алгебраическое уравнение относительно изображения F (p)= L [ f (t)]. Решив это алгебраическое уравнение и найдя F (p), мы получим изображение решения исходного дифференциального уравнения. Для определения самого решения можно воспользоваться обратным преобразованием Лапласа (L –1–преобразованием), устанавливающим связь между изображением F (p) и оригиналом f (t):
где с = R ep. Функция f (t) может считаться оригиналом, если выполняются следующие условия: 1) Функция f (t) непрерывна для всех значений t ³ 0. Непрерывность может быть нарушена лишь в отдельных точках, являющихся точками разрыва непрерывности первого рода, причем число этих точек должно быть конечным на любом интервале ограниченной длины. 2) Функция f (t) = 0 для значений t < 0. 3) Функция f (t) имеет ограниченный порядок возрастания, т.е. можно указать такие постоянные числа М > 0 и с о ³ 0, при которых выполняется неравенство 5.1.1. Основные свойства преобразования Лапласа
1. Линейность преобразования а) постоянный коэффициент выносится за знак преобразования Лапласа
б) преобразование Лапласа суммы функций равно сумме преобразований Лапласа (принцип суперпозиции)
2. Преобразование Лапласа от функции, у которой переменная t умножена на постоянное число а определяется выражением
3. Дифференцирование оригинала
где Если начальные условия нулевые, т.е.
то
4. Интегрирование оригинала
где
Если начальные условия нулевые, то
5. Конечное значение функции
6. Начальное значение функции
7. Формула запаздывания
5.1.2. Примеры преобразования Лапласа для типовых функций
1. f (t) = C, где С = const
2.
и т.д. Получены соответствующие таблицы изображений по Лапласу для определенных функций (оригиналов)
Фрагмент таблицы изображений по Лапласу простейших функций
5.1.3. Решение линейных дифференциальных уравнений с помощью преобразования Лапласа Метод операционного исчисления заключается в том, что в общем случае решение исходной системы дифференциальных уравнений, которым подчиняются искомые оригиналы, заменяется решением соответствующей системы уравнений для изображений. В том случае, когда исходные уравнения для оригиналов являются обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами, соответствующие им уравнения оказываются алгебраическими. Из алгебраических уравнений изображение искомого оригинала находится путем элементарных алгебраических преобразований. При этом отпадают громоздкие вычисления, возникающие в классическом методе в связи с определением произвольных постоянных интегрирования в соответствии с заданными начальными условиями, так как в операторном методе начальные условия автоматически вводятся в изображение решения. Оригинал решения при известном его изображении обычно может быть легко найден путем использования обширных таблиц. С другой стороны, изучение свойств изображения искомого решения уже позволяет установить весьма общие и важные для практики свойства самой системы.
Примеры 1. Найти решение уравнения
с начальными условиями: при t = 0, x (0) = 0, Преобразуем каждый член этого уравнения по Лапласу. Положим L [ x (t)] = X (p) и используем соответствующие свойства и формулы.
После преобразования по Лапласу исходное дифференциальное уравнение станет алгебраическим относительно изображения Х (р):
Найдем Х (р):
где корни знаменателя р 1 = -1 и р 2 = -2, поэтому Х (р) можно представить в виде суммы элементарных слагаемых:
Здесь K 1 = 1; K 2 = -1. Для определения оригинала х (t), выполним обратное преобразование Лапласа.
5.2. Понятие передаточной функции Метод преобразования Лапласа оказался мощным инструментом для решения линейных дифференциальных уравнений. Кроме того, с целью упрощения методов расчета и проектирования линейных систем автоматического регулирования было признано целесообразным уравнения динамики объектов управления и управляющих устройств записывать не через оригиналы функций, а в виде их изображений, получаемых с помощью прямого преобразования Лапласа, и в виде продукта этого преобразования – через так называемые передаточные функции. Передаточная функция W (p) – это отношение изображений (по Лапласу) выходной величины САУ к входной при нулевых начальных условиях, т.е.
Предположим, что система описывается уравнением вида:
Получим преобразование Лапласа от левой и правой частей:
Преобразование Лапласа линейно и поэтому: 1) преобразование от суммы равно сумме преобразований от слагаемых; 2) постоянный коэффициент можно выносить за знак преобразования Лапласа. Из 1–го свойства следует:
Из 2–го свойства следует:
Предположим, что начальные условия нулевые, т.е. при t = 0,
В этом случае преобразование Лапласа от производной имеет вид:
Тогда уравнение (*) можно переписать следующим образом:
Если вынести за скобки L [ x ] и L [ f ], то получим
L [ x ](anрn + … a 1 р + a o) = L [ f ](b mрm + … b 1 р + b o).
Откуда
или
Многочлен числителя К (р) = bmpm + … + b 1 p + b o называется оператором воздействия. Многочлен знаменателя D (p) = anpn + … + a 1 p + a o называется собственным (характеристическим) оператором системы. Его вид не зависит от внешних воздействий, а выражение D (p) = 0 называется характеристическим уравнением системы.
5.3. Временные и частотные характеристики САУ Динамические свойства (поведение в переходном режиме) отдельных элементов САУ или системы в целом могут быть описаны дифференциальными уравнениями или передаточными функциями, соответствующими этим уравнениям. Очень часто при решении различных задач анализа и синтеза удобнее использовать графическое представление этих свойств в виде характеристик различного типа. Чаще всего применяют две группы таких характеристик – временные и частотные характеристики. Характеристики могут быть сняты экспериментально или построены по дифференциальному уравнению или передаточной функции системы. С помощью этих характеристик можно определить реакцию системы на возмущение произвольного типа.
5.3.1. Временные характеристики САУ Существуют различные виды временных характеристик. Они показывают поведение системы во времени при нанесении внешнего воздействия определенного вида. В качестве временной характеристики чаще всего рассматривают реакцию САУ на единичное ступенчатое изменение входного сигнала f (t):
Эту временную характеристику называют переходной характеристикой h (t), причем ее можно получать экспериментально или расчетным путем. При экспериментальном определении h (t) предполагается, что САУ оборудована специальным устройством, позволяющим произвольным образом изменить f (t), и устройством, предназначенным для автоматической записи выходной величины системы x (t). Перед проведением эксперимента стабилизируют все переменные САУ и затем в определенный момент времени ступенчато изменяют на одну условную единицу входной сигнал f (t). В дальнейшем f (t) не изменяется. Этот момент времени считают нулевым и с этого момента времени с помощью самописца регистрируют кривую изменения выходной величины. Полученная кривая будет характеристикой h (t). При расчетном способе определения h (t) решают дифференциальное уравнение САУ для f (t) = 1(t). В определенных случаях для получения h (t) необходимо использовать так называемую формулу Хевисайда. Предполагается, что передаточная функция САУ имеет вид:
или
и тогда уравнение Хевисайда принимает вид:
где К (0) = [ К (р)] р =о; D (0) = [ D (p)] р =о,
р 1, р 2, …, рi, …, рn – корни характеристического уравнения D (p) = 0. Формула в таком виде применима, если корни характеристического уравнения действительные и разные. В противном случае используется соответствующий вариант формулы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.180.88 (0.011 с.) |

 .
. , t > 0
, t > 0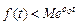 (t > 0).
(t > 0). ;
; .
. .
. ,
, – значения функции и ее производных при t=0 (учитывают начальные условия).
– значения функции и ее производных при t=0 (учитывают начальные условия). ,
,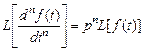 .
. ,
, при t = 0;
при t = 0; при t=0.
при t=0. .
. .
. .
. .
. .
.
 ;
;




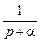



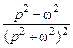

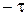 )
)

 ,
, .
.

 .
. .
. ,
, ,
, .
.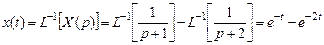 (t ³ 0).
(t ³ 0). ,
,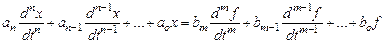 .
. .
. .
.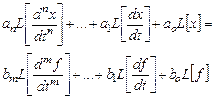 . (*)
. (*) .
. ,
,


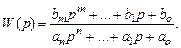

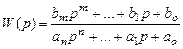


 ,
,  ,
,


