
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Северо–кавказский горно–металлургический институтСодержание книги
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ СЕВЕРО–КАВКАЗСКИЙ ГОРНО–МЕТАЛЛУРГИЧЕСКИЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ)
Кафедра теории и автоматизации металлургических Процессов и печей
МАТЕМАТИЧЕСКИЕ ОСНОВЫ АВТОМАТИКИ
Допущено редакционно–издательским советом Северо–Кавказского горно–металлургического института (государственного технологического университета) в качестве конспекта лекций для студентов специальности 22301.65 «Автоматизация технологических процессов и производств» (по отраслям)
Владикавказ 2008 УДК 519.71:681.5
Рецензент: Рутковский А. Л.
Текиев В. М. Математические основы автоматики: Конспект лекций. –Владикавказ: Издательство СКГМИ (ГТУ) "Терек", 2008. с.
Редактор Иванченко Н. К. Компьютерная верстка Цишук Т. С.
УДК 519.71; 681.5
Ó Издательство СКГМИ (ГТУ) "Терек", 2008 Сдано и подписано в печать 28.10.08. Формат 60x84 1/16. Объем 5,39 усл. п.л. Тираж 75 экз. Заказ № Отдел оперативной полиграфии СКГМИ (ГТУ).
Тема 1. Случайные события и случайные величины, их Числовые характеристики 1.1. Математические модели эксперимента, учитывающие случайный разброс его результатов Все процессы, происходящие в природе, являются результатом взаимодействия многих факторов. Для того чтобы изучить эти процессы и в дальнейшем ими управлять, необходимо выяснить, какую роль в рассматриваемом процессе играет каждый фактор в отдельности. Все эти факторы необходимо выразить в каких–либо количественных оценках. Для этого используют математические методы и чтобы получить необходимые числовые данные, нужно произвести серию наблюдений. Однако даже самый тщательно подготовленный эксперимент не позволяет выделить интересующий нас фактор в чистом виде. Мы не в силах изолировать многие посторонние факторы: изучая химические реакции, мы никогда не имеем дела с чистыми веществами; изучая электронные процессы, не можем вести их в абсолютном вакууме и т.д. Наконец, нужно вспомнить о различных помехах, связанных с окружающей обстановкой – ведь даже шум идущего по улице автомобиля сказывается на проводимом в лаборатории эксперименте.
Следовательно, каждое наблюдение дает нам лишь результат взаимодействия основного изучаемого фактора с многочисленными посторонними. Некоторые их этих факторов можно учесть, так как они сами по себе достаточно изучены. Учет других факторов (например, наличие примесей в веществах) может быть очень громоздким. Он сильно затягивает эксперимент, делает его неоправданно дорогим. Наконец, многие факторы (помехи) бывают настолько неожиданными, что их вообще нельзя учесть. Сюда следует отнести и те факторы, о которых на данном этапе развития науки вообще ничего не известно. Вывод: полное и точное описание какого–либо процесса возможно лишь в том случае, если известны все факторы, влияющие на этот процесс. Иными словами, такое описание вообще невозможно. К счастью, оно и не нужно! Так все применяемые в эксперименте измерительные приборы обладают некоторым пределом точности – минимальной разницей в значениях двух величин, которую они в состоянии обнаружить. Этот предел обычно указывается на приборах, изготовленных в заводских условиях. Например, аналитические весы, взвешивающие с точностью до 0,1 мг, не смогут различить такие веса, как 12,52 и 12,54 мг, и в обоих случаях покажут 12,5 мг. В результате все дальнейшие вычисления, связанные с этими данными, также будут содержать некоторую неточность, даже если пользоваться абсолютно точными и полными формулами, описывающими исследуемый процесс. Таким образом, в наших наблюдениях всегда допускается некоторая «законная» неточность, величину которой можно рассчитать заранее. Благодаря этому мы можем не учитывать те посторонние факторы, действие которых намного меньше этой неточности. По этой же причине удается избежать детального исследования многочисленных непредвиденных (случайных) помех. Хотя действие каждой из них может оказаться вполне заметным, в общей массе они как правило, уравновешивают друг друга, лишь изредка давая заметный суммарный эффект. Установлено, что случайные, непредвиденные события в массе своей подчиняются некоторым общим неслучайным закономерностям. Наука, изучающая закономерности массовых случайных явлений, называется теорией вероятностей. Применение теории вероятностей к обработке больших совокупностей чисел называется математической статистикой.
Использование методов математической статистики в обработке наблюдений оказывается весьма плодотворным. Никакие теории при наличии непредвиденных и случайных факторов не могут давать точные и однозначные ответы. Основная задача математической статистики при обработке наблюдений – оценить риск той или иной ошибки в полученном результате. Принять или не принять риск – дело исследователя. В том случае, если этот риск его не устраивает, он должен найти пути его уменьшения: применить более точную методику наблюдений, устранить наиболее заметные помехи и т.д. Теория вероятностей отвлекается от всех физических особенностей изучаемого явления, кроме его случайности. Поэтому применение теории вероятностей к обработке наблюдений приводит нередко к очень грубым оценкам и ее выводы следует использовать очень осторожно, в то же время применение этих методов почти всегда связано с большим объемом вычислений. К категории случайных явлений можно отнести все те явления, точное предсказание протекания которых в каждом отдельном случае оказывается невозможным. Однако, если вместо того, чтобы рассматривать каждое из случайных явлений в отдельности, мы обратимся к совокупности большого их числа, то окажется, что средние результаты обнаруживают своего рода устойчивость. В теории вероятностей рассматриваются три класса случайных явлений: случайные события; случайные величины; случайные функции. Случайные события
Событие, которое при заданном комплексе факторов может либо произойти, либо не произойти, называется случайным событием. Примеры: 1. Выпадение герба при бросании монеты. 2. Попадание в цель при выстреле. Различные события мы будем обозначать буквами А, В, … Событие называют достоверным, если оно непременно должно произойти. Например – появление электрического тока в замкнутой цепи с хорошим источником ЭДС. Событие называют невозможным, если оно заведомо не наступит. Пример: ток в разомкнутой цепи. Пусть А – некоторое событие. Под событием, противоположным ему будем понимать событие, состоящее в том, что А не наступило, обозначим его Событие называют единственно возможным, если в результате каждого испытания хотя бы одно из них наверное наступит. Эти события образуют полную группу событий. Вероятность события
Свойства вероятности
1. Вероятность любого события А подчинена условиям 0 £ Р (А) £ 1, так как 0 £ m £ n. 2. Вероятность достоверного события Е: Р (Е) = 1, так как m = n. 3. Вероятность невозможного события U: Р (U) = 0, так как m = 0.
Полная вероятность
Пусть события Н1, Н2,…, Нn образуют полную группу событий и при наступлении каждого из них (Нi) событие А может наступить с некоторой условной вероятностью В соответствии с теорией умножения найдем, что вероятность наступления А при условии Н 1, Н 2,…, Нn: Р (Н 1 и А) = Р (Н 1) ………………………….. Р (Нn и А) = Р (Нn)
По теореме сложения (события Н1, Н2,… несовместны):
Пример. При разрыве снаряда образуются крупные, средние и мелкие осколки, причем число крупных осколков составит 0,1 их общего числа; средних – 0,3; мелких – 0,6. При попадании в танк крупный осколок прибивает броню с вероятностью 0,9; средний – 0,3; мелкий – 0,1. Какова вероятность того, что попавший в броню осколок пробьет ее?
1.3. Случайные величины Под случайной величиной понимается величина, принимающая в результате опыта какое–либо числовое значение из множества возможных значений. Примеры: 1) Число выстрелов, произведенных до первого попадания в цель (любое целое положительное число). 2) Расстояние от центра мишени до точки попадания (любое положительное число или 0).
Случайная величина, принимающая конечное число или последовательность различных значений, называется дискретной случайной величиной (пример 1). Случайная величина принимающая все значения из некоторого интервала, называется непрерывной случайной величиной (пример 2). Чтобы охарактеризовать дискретную случайную величину, прежде всего необходимо указать возможные ее значения. Однако этого недостаточно: нужно еще знать, насколько часто принимаются различные значения этой величины, что лучше всего характеризовать вероятностью отдельных ее значений. Иначе говоря, для случайной величины Х следует указывать не только ее значения x 1, x 2,…, x n, но и вероятности событий X = xi, р i = P (X = x i), (i = 1,2,…, n) состоящих в том, что случайная величина Х приняла значение хi. Если перечислены все возможные значения X, то события X = xi не только несовместны, но и единственно возможны, так что сумма заданных вероятностей рi должна равняться единице. Соотношение, устанавливающее связь между значениями случайной величины и вероятностями этих значений, называется законом распределения случайной величины. Для дискретной случайной величины закон распределения удобно записывать в виде таблицы, причем
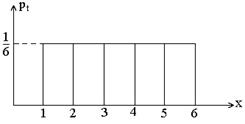
Иногда этот закон задают в виде графика: по оси абсцисс откладывают возможные значения случайной величины Х, а по оси ординат – соответствующие значения вероятностей. Получаемая при этом ломаная линия называется многоугольником распределения. Пример: Х – число очков, выпадающих на игральной кости. Возможные значения 1,…,6 равновероятны. Закон распределения:
Многоугольник распределения:
Откуда P (a< X <b)= Р (Х <b)
Исходя из определения функции распределения:
Определим вероятность Р (Х = a):
Если функция F (х) непрерывна, то последний предел равен нулю: Р (Х = a) = 0. Т.е., если функция распределения случайной величины непрерывна, то вероятность того, что случайная величина примет заранее заданное значение, равна нулю, но это событие не является невозможным. Примеры законов распределения случайной величины
Рассмотрим примеры распределения случайной величины.
1 .4.1. Равномерное распределение дискретной случайной величины При бросании игральной кости может выпасть 1,2,3,… или 6. Здесь величина Х принимает значения хi = i с вероятностями соответственно
Рассчитаем для этой случайной величины математическое ожидание М [ X ] и дисперсию D [ X ]:
При этом
1.4.2. Равномерное распределение непрерывной случайной величины
Предположим, что случайная величина имеет равномерное и непрерывное распределение. Причем ее плотность вероятности
или
Случайная величина называется непрерывной, если ее функция распределения F (x) непрерывна на всей числовой оси, а плотность вероятности j(x) существует и непрерывна всюду, кроме дискретного множества точек. Для нахождения функции распределения F (x) воспользуемся формулой
При x £ a Для а < x < b получим
Наконец при х ³ b получим:
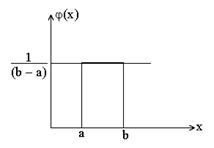
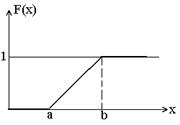
Таким образом интегральный закон равномерного распределения случайной величины задается формулой
и соответственно в виде графика:
Числовые характеристики непрерывной случайной величины
1.4.3. Нормальный закон распределения (закон Гаусса) Среди законов распределения, которым подчиняются встречающиеся на практике случайные величины, чаще всего приходиться иметь дело с нормальным законом распределения. Это предельный закон, к которому приближаются многие другие законы распределения при определенных условиях. Если случайную величину можно рассматривать как результат суммарного воздействия многих независимых факторов, то закон распределения такой случайной величины будет близок к нормальному. Для этого закона плотность вероятности задается формулой:
Выясним геометрический смысл параметров «а» и «s» (а – математическое ожидание; s2 – дисперсия, s – среднеквадратическое отклонение). Из формулы видно, что кривая у = j(х) достигает максимума при х = а, причем максимальное значение
При
И корреляционный анализ 2.1. Выборочный метод
Применение математической статистики к обработке наблюдений оказывается возможным благодаря использованию выборочного метода. Выборочный метод в самой общей форме выглядит следующим образом. Имеется некоторая большая совокупность объектов, называемая генеральной совокупностью. Из этой совокупности извлекается n объектов, которые образуют выборку; число n называется объемом выборки. Эти n объектов подвергаются детальному исследованию, по результатам которого требуется описать всю генеральную совокупность или какие–нибудь ее свойства, характеристики. Пример. Завод, выпускающий электролампы, должен контролировать свою продукцию, в частности, проверять долговечность ламп. Чтобы проверить срок службы лампы, нужно держать ее на испытательном стенде включенной до тех пор, пока она не перегорит. Если бы завод проверял все свои лампы, то его продукция не пошла бы дальше стенда. Из создавшегося положения находят простой выход: отбирают, скажем, одну лампу на тысячу и проверяют только отобранные лампы. В этом случае по долговечности ламп из выборки судят о долговечности всей генеральной совокупности выпускаемых заводом ламп.
Получается следующая схема производства наблюдений: имеется случайная величина Х и в результате n независимых испытаний получаются n ее допустимых значений. Если все допустимые значения случайной величины Х считать генеральной совокупностью, то полученные при наблюдениях n значений образуют выборку. По этой выборке мы и должны определить распределение случайной величины Х (т.е. распределение генеральной совокупности). При наблюдениях получают числа х 1, х 2,…, хn (элементы выборки). Их можно считать полной совокупностью значений некоторой конечнозначной случайной величины Хn и конечное распределение Хn называют выборочным (эмпирическим) распределением. Доказано: с вероятностью равной единице максимальная разность между функциями распределения случайных величин Х n и Х при n ® ¥ стремится к нулю. Практически это означает, что при достаточно большом объеме выборки функцию распределения генеральной совокупности можно приближенно заменять выборочной функцией распределения.
Среднее и дисперсия выборки
Пусть М [ Х ] – математическое ожидание случайной величины Х. Это число нам неизвестно. Мы проводим наблюдения и при большом объеме выборки n можно вместо М [ Х ] рассматривать математическое ожидание Хn. Погрешность при этом будет тем меньше, чем больше объем выборки n. Математическое ожидание выборки есть просто среднее арифметическое элементов выборки:
Будем называть средним выборки
где х i – варианта выборки; n i – частота варианты х i; n – объем выборки. Таким образом, в качестве истинного результата можно брать Дисперсия D [ Х ] приближенно равна дисперсии D [ Xn ].
т.е. D [ Х ]» D [ X n]. Это равенство было бы еще более надежным, если бы в формуле для D [ X n] вместо
которая является несмещенной оценкой дисперсии. Переход к несмещенной оценке S 2 важен в основном для малых выборок, ибо разница между S 2 и D [ X n] при больших n незаметна. Таким образом, среднее выборки
а несмещенная оценка дисперсии выборки
В практических вычислениях для дисперсии S 2 часто удобна формула
Величина S (корень квадратный из выборочной дисперсии) называется средним квадратическим отклонением выборки или выборочным стандартом. Почему в формуле дисперсии n заменили на n – 1? Это связано с тем, что входящая в формулу величина Каждая величина, зависящая от элементов выборки и участвующая в формуле выборочной дисперсии, называется связью. Эта разность показывает, какое количество элементов выборки можно произвольно изменять, не нарушая связей и называется числом степеней свободы. Таким образом, знаменатель выборочной дисперсии всегда равен разности между объемом выборки и числом связей, наложенных на эту выборку. 2.2. Связь между случайными величинами. Корреляция До сих пор изучали наблюдения над одной случайной величиной. Между тем для выяснения тех или иных причинно–следственных связей в окружающей природе необходимо вести одновременные наблюдения над целым рядом случайных величин, чтобы по полученным данным изучать взаимоотношения этих величин. Ограничимся пока двумя случайными величинами Х и У. В математическом анализе зависимость между двумя величинами выражается понятием функции у = f (x), где каждому допустимому значению одной переменной соответствует одно и только одно значение другой переменной. Такая зависимость называется функциональной, она обнаруживается с помощью строгих логических доказательств и не нуждается в опытной проверке. Если у = const при изменении х, то говорят, что у не зависит от х. Гораздо сложнее обстоит дело с понятием зависимости случайных величин: если при изменении х изменилось у, мы не можем сказать, является ли это изменение результатом зависимости у от х или это результат влияния случайных факторов. Здесь имеет место связь особого рода, при которой с изменением одной величины меняется распределение другой – такая связь называется стохастической. Выявление стохастической связи и оценка ее силы представляют задачу математической статистики. Рассматривая свойства дисперсии, мы указали, что дисперсия суммы двух независимых величин равна сумме дисперсий этих величин. Поэтому если для двух случайных величин Х и У окажется, что
то это служит верным признаком наличия зависимости между Х и У, т.е. корреляции. Из этого неравенства вытекает (доказано), что справедливо следующее неравенство:
где Корреляционный момент зависит от единиц измерения величин Х и У. Поэтому на практике чаще используется безразмерная величина, которая называется коэффициентом корреляции.
2.2.1. Свойства коэффициента корреляции 1. Коэффициент корреляции независимых или некоррелированных величин равен нулю. 2. Коэффициент корреляции не меняется от прибавления к Х или У каких–либо постоянных (неслучайных) слагаемых, от умножения их на положительные числа. 3. Если одну из случайных величин, не меняя другой, умножить на 4. Численно коэффициент корреляции заключен в пределах 5. Если r > 0, то величины Х и У с точностью до случайных погрешностей одновременно возрастают или убывают, если же r < 0, то с возрастанием одной величины другая убывает. Но это справедливо только для линейной зависимости У от Х. Т.е. зависимость между Х и У может быть строго функциональной (например, квадратичной) без следа случайности, а коэффициент корреляции все еще будет меньше 1. Таким образом, коэффициент корреляции есть показатель того, насколько связь между случайными величинами близка к строгой линейной зависимости. Он одинаково отмечает и слишком большую долю случайности, и слишком большую криволинейность этой связи. Если заранее, из общих соображений, можно предсказать линейную зависимость, то r является достаточным показателем тесноты связи между Х и У. Для случайных величин (большинство именно таких), подчиняющихся нормальному закону, равенство r = 0 означает одновременно и отсутствие всякой зависимости.
Наблюдений
Допустим, что проведено n испытаний и при каждом отмечались значения двух случайных величин. В результате получается n пар выборочных значений (х 1, у 1), (х 2, у 2),…, (х n, у n). Для наглядности эти пары значений можно рассматривать как координаты точек на плоскости. Образовавшаяся совокупность точек сразу же дает представление о силе корреляции, где
а - сильная корреляция; в - слабая корреляция; с - отсутствие корреляции Выборочный коэффициент корреляции r вычисляется по той же формуле, что и генеральный коэффициент r, только здесь берутся выборочные математические ожидания (средние) и дисперсии. Если через
то выборочный корреляционный момент равен
откуда
где через
Удобнее при вычислениях пользоваться следующими выражениями:
В связи со случайностью выборки выборочный коэффициент корреляции r может быть отличен от нуля, даже если между наблюдаемыми величинами нет корреляции. Следовательно, для проверки гипотезы об отсутствии корреляции необходимо проверять, значительно ли r отличается от нуля. 2.2.3. Частная линейная корреляция
Одним из методов исследования линейной связи между тремя (или несколькими) признаками, измеряемыми единовременно у некоторых элементов, является линейная корреляция, применяемая в случае равнозначности признаков, когда неудобно делить их на независимые и зависимые случайные переменные (как это было сказано раньше). При этом различают частную линейную и множественную линейную корреляции. Обозначим эти признаки Х, У, Z. Например: исследуют свойства некоторого сорта стали: Х – предел текучести, У – предел прочности, Z – предел упругости. Рассматривая каждый раз только по два из трех признаков, можно в качестве меры линейной зависимости вычислить эмпирические простые коэффициенты корреляции rху, rxz, rуz (аналогично расчетам, соответствующим парной корреляции). При рассмотрении более двух признаков, однако, для получения безупречного статистического решения простых коэффициентов корреляции оказывается уже недостаточно. Так, rxz выражает зависимость между Х и Z. Но она может возникнуть и по той причине, что оба признака в большей или меньшей мере подвержены воздействию третьего признака – У. Чтобы исключить влияние третьей случайной величины на две другие, вводят эмпирические частные коэффициенты корреляции, обозначенные через Буквы перед точкой указывают, между какими признаками изучается зависимость, а буква после точки – влияние какого признака исключается. Разумеется Принятые обозначения легко распространить на частные коэффициенты корреляции для числа признаков больше трех и выражать линейную связь только между двумя признаками, исключая каждый раз воздействие остальных. Частные коэффициенты корреляции рассчитываются по простым коэффициентам корреляции согласно формулам
Второе и третье уравнения выводятся из первого путем циклической перестановки букв х, у, z. Подобно простым коэффициентам корреляции частные коэффициенты могут принимать значения, заключенные между –1 и +1. Частные коэффициенты корреляции в большей или меньшей степени отклоняются от простых коэффициентов корреляции в зависимости от того, какое воздействие третий, исключаемый, признак оказывает на два оставшихся.
2.2.4. Множественная линейная корреляция Для ответа на вопрос, зависит ли один из признаков одновременно от двух других (или у от х 1 и х 2 при взаимном влиянии х 1 и х 2), вводятся эмпирические множественные коэффициенты корреляции Для практических расчетов обычно применяют следующую формулу:
Аналогично для других зависимостей.
2.3. Регрессия Корреляционный анализ служит установлению значимости (неслучайности) изменения наблюдаемой случайной величины в процессе испытаний. Следующей, еще более высокой ступенью должно явиться выяснение точных количественных характеристик изменения случайной величины. Подобно тому, как совокупность значений случайной величины описывалась набором неслучайных параметров, так и стохастическую, т.е. содержащую элемент случайности, связь нужно научиться выражать через строгие функциональные (неслучайные) соотношения. Т.е. требуется установить зависимость некоторой случайной величины У от параметра Х, т.е. у от х, которая называется регрессией. Имеется выборка (х 1, у 1), (х 2, у 2),…, (хn, yn) и нужно найти уравнение приближенной регрессии, которое запишем как у = f (x). В качестве принципа приближенности обычно используют принцип наименьших квадратов, который формулируется так: Пусть задан некоторый класс функций f (x), накладывающих на выборку одинаковое число связей. Тогда наилучшее уравнение приближенной регрессии дает та функция из рассматриваемого класса, для которой сумма квадратов
имеет наименьшее значение. Принцип наименьших квадратов позволяет полностью вычислить уравнение приближенной регрессии заданного типа (с неопределенными коэффициентами). Например уравнение регрессии имеет вид:
Составляется сумма
Эти равенства можно рассматривать как уравнения относительно a, b, g…; которые в математической статистике называются нормальными уравнениями. Доказано, что так как величина S ³ 0 при любых a, b, g…, то у нее обязательно должен существовать хотя бы один минимум и, если система нормальных уравнений имеет единственное решение, то оно и является минимальным для величин S, и никаких дополнительных исследований проводить не нужно. Использу
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.178.1 (0.018 с.) |

 362021. Владикавказ, ул. Николаева, 44.
362021. Владикавказ, ул. Николаева, 44.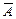 . События А и В называют несовместными, если наступление одного из них исключает возможность наступления другого. Например: появление четного и нечетного чисел одновременно при бросании кости невозможно.
. События А и В называют несовместными, если наступление одного из них исключает возможность наступления другого. Например: появление четного и нечетного чисел одновременно при бросании кости невозможно.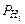 (А). Какова будет при этом вероятность наступления события А?
(А). Какова будет при этом вероятность наступления события А?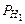 (А)
(А)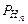 (А).
(А).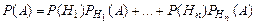 или
или – это так называемая формула полной вероятности.
– это так называемая формула полной вероятности.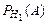 = 0,9
= 0,9
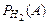 = 0,3
= 0,3
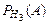 = 0,1
= 0,1
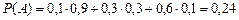 .
.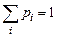 .
.
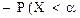 ).
).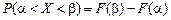 .
.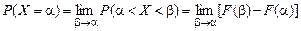 .
.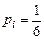 (i = 1, 2, 3…, 6). Ввиду равенства всех вероятностей можно говорить о равномерном распределении случайной величины Х.
(i = 1, 2, 3…, 6). Ввиду равенства всех вероятностей можно говорить о равномерном распределении случайной величины Х.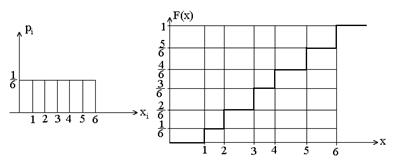

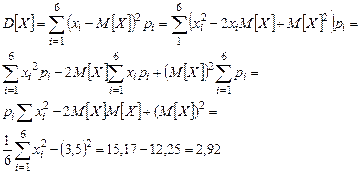
 .
.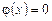 для всех значений, кроме интервала (a, b), на котором она постоянна. Постоянное значение обозначим через A. Тогда можно записать
для всех значений, кроме интервала (a, b), на котором она постоянна. Постоянное значение обозначим через A. Тогда можно записать
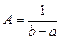 . Поэтому плотность равномерного распределения задается формулой
. Поэтому плотность равномерного распределения задается формулой
 .
.
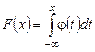 .
. . Тогда F (x) = 0.
. Тогда F (x) = 0.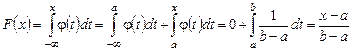 .
.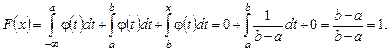
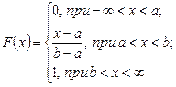
 .
.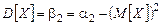 ;
; ;
;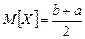 ;
; 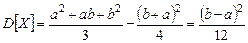 .
.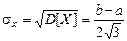 .
.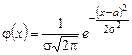 .
. . С ростом s величина максимального значения уменьшается, а так как площадь, ограниченная всей кривой и осью абсцисс, равна единице, то с ростом s кривая как бы растягивается вдоль оси ох и наоборот. Приведены графики у = j(х) при различных «а», но при одном и том же s. На другом – при а = 0, но различных s.
. С ростом s величина максимального значения уменьшается, а так как площадь, ограниченная всей кривой и осью абсцисс, равна единице, то с ростом s кривая как бы растягивается вдоль оси ох и наоборот. Приведены графики у = j(х) при различных «а», но при одном и том же s. На другом – при а = 0, но различных s. имеет место предел, когда j = 0 (по формуле). Разность (х
имеет место предел, когда j = 0 (по формуле). Разность (х 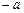 ) содержится в формуле в квадрате, т.е. график функции симметричен относительно прямой х = а.
) содержится в формуле в квадрате, т.е. график функции симметричен относительно прямой х = а.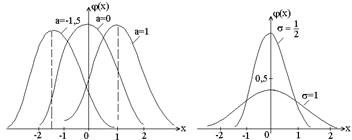
 .
. . Если сгруппировать итоги наблюдений, то можно записать
. Если сгруппировать итоги наблюдений, то можно записать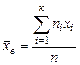 ,
, ,
, ,
, ,
, .
. .
. ,
,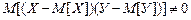 ,
, называют корреляционным моментом.
называют корреляционным моментом. .
. , то на
, то на 
 и
и  обозначить средние значения для хi и yi:
обозначить средние значения для хi и yi: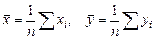 ,
, ,
, ,
, и
и  обозначены выборочные дисперсии
обозначены выборочные дисперсии
 ,
,
 ,
, .
. .
.

 .
. ,
, ,
, .
. . Они являются мерой линейной связи между одним из признаков (буква индекса перед точкой) и совокупностью других признаков. Эти коэффициенты заключены в переделах –1 и +1.
. Они являются мерой линейной связи между одним из признаков (буква индекса перед точкой) и совокупностью других признаков. Эти коэффициенты заключены в переделах –1 и +1. .
.

 , …
, …


