Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние значения случайных величинСодержание книги
Поиск на нашем сайте
Предположим, что Х – дискретная случайная величина, которая в результате эксперимента принимала значения x 1, x 2,…, xn с вероятностями p 1, p 2,…, pn, Пример. Определить среднее значение ошибки регулирования e, если на основании большого числа опытов установлено, что вероятность ошибки рi равна:
Решение:
1. M [e] = 0,1×0,2 + 0,15×0,2 + 0,2×0,3 + 0,25×0,15 + 0,3×0,15 = = 0,19 %.
В том случае, если g(Х) является функцией X (причем вероятность того, что X = xi равна pi), то среднее значение функции определяется как
Предположим, что X – случайная величина с непрерывным распределением и характеризуется плотностью вероятности j(x). Тогда вероятность того, что X заключена между x и x + D х:
Величина X при этом приближенно принимает значение x. В пределе при D x ® 0, можно предположить, что приращение D x численно равно дифференциалу d x. Произведя замену D x = d х, получаем точную формулу для расчета среднего значения Х: Аналогично для g(Х): Как правило, недостаточно бывает знать только среднее значение (математическое ожидание) случайной величины. Для оценки меры случайности величины (для оценки разброса конкретных значений X относительно математического ожидания M [ X ]) вводится понятие дисперсии случайной величины. Дисперсия – среднее значение квадрата отклонения каждого конкретного значения X от математического ожидания. Чем больше дисперсия
Для непрерывной случайной величины дисперсию можно записать аналогично:
Дисперсия 1.3.2.1. Свойства математического ожидания 1. Математическое ожидание неслучайной величины равно самой этой величине M [ C ] = C. 2. Неслучайный множитель С можно выносить за знак математического ожидания M [ CX ] = CM [ X ].
3. Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин.
4. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин (условие независимости случайных величин).
1.3.2.2. Свойства дисперсии 1. Дисперсия неслучайной величины С равна нулю: D [ C ]=0. 2. Дисперсия произведения неслучайного множителя С на случайную величину равна произведению С 2 на дисперсию случайной величины.
3. Дисперсия суммы независимых случайных величин X 1 и X 2 равна сумме дисперсий слагаемых 1.3.3. Моменты случайной величины Пусть Х – непрерывная случайная величина. Если n – целое положительное число, а функция x n интегрируема на интервале (–¥; +¥), то среднее значение
называется начальным моментом порядка n случайной величины X. Очевидно, что момент нулевого порядка
а начальный момент первого порядка
есть математическое ожидание самой случайной величины Х. Момент второго порядка
есть математическое ожидание квадрата случайной величины Х. Аналогично находят a2, a3 и т.д. Если
Есть связь между начальными и центральными моментами. Так bо = aо b2=a2 b3=a3
Примеры законов распределения случайной величины
Рассмотрим примеры распределения случайной величины.
1 .4.1. Равномерное распределение дискретной случайной величины При бросании игральной кости может выпасть 1,2,3,… или 6. Здесь величина Х принимает значения хi = i с вероятностями соответственно
Рассчитаем для этой случайной величины математическое ожидание М [ X ] и дисперсию D [ X ]:
При этом
1.4.2. Равномерное распределение непрерывной случайной величины
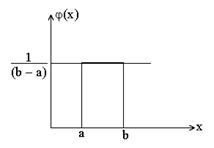
Предположим, что случайная величина имеет равномерное и непрерывное распределение. Причем ее плотность вероятности
или
Случайная величина называется непрерывной, если ее функция распределения F (x) непрерывна на всей числовой оси, а плотность вероятности j(x) существует и непрерывна всюду, кроме дискретного множества точек. Для нахождения функции распределения F (x) воспользуемся формулой
При x £ a Для а < x < b получим
Наконец при х ³ b получим:
Таким образом интегральный закон равномерного распределения случайной величины задается формулой
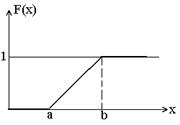
и соответственно в виде графика:
Числовые характеристики непрерывной случайной величины
1.4.3. Нормальный закон распределения (закон Гаусса) Среди законов распределения, которым подчиняются встречающиеся на практике случайные величины, чаще всего приходиться иметь дело с нормальным законом распределения. Это предельный закон, к которому приближаются многие другие законы распределения при определенных условиях. Если случайную величину можно рассматривать как результат суммарного воздействия многих независимых факторов, то закон распределения такой случайной величины будет близок к нормальному. Для этого закона плотность вероятности задается формулой:
Выясним геометрический смысл параметров «а» и «s» (а – математическое ожидание; s2 – дисперсия, s – среднеквадратическое отклонение). Из формулы видно, что кривая у = j(х) достигает максимума при х = а, причем максимальное значение При
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.160 (0.009 с.) |

 . Тогда средним значением или математическим ожиданием величины X называется сумма
. Тогда средним значением или математическим ожиданием величины X называется сумма  , т.е. средневзвешенное значение величины Х, где весами служат вероятности pi.
, т.е. средневзвешенное значение величины Х, где весами служат вероятности pi.
 .
.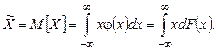

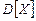 , тем больше случайности разброса величины от математического ожидания. Если случайная величина дискретная, то
, тем больше случайности разброса величины от математического ожидания. Если случайная величина дискретная, то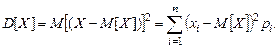
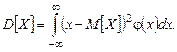
 хорошо описывает разброс величины, но при этом есть один недостаток: размерность
хорошо описывает разброс величины, но при этом есть один недостаток: размерность 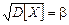 , которое называется средним квадратическим отклонением.
, которое называется средним квадратическим отклонением. .
.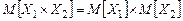 .
.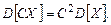
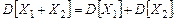
 n = 0, 1,…, n
n = 0, 1,…, n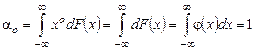 ,
, ,
,
 – центрированная случайная величина, то представляет интерес рассмотрение центральных моментов порядка n, где n = 0, 1,…, n:
– центрированная случайная величина, то представляет интерес рассмотрение центральных моментов порядка n, где n = 0, 1,…, n: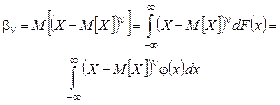


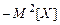
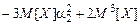 и т.п.
и т.п.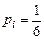 (i = 1, 2, 3…, 6). Ввиду равенства всех вероятностей можно говорить о равномерном распределении случайной величины Х.
(i = 1, 2, 3…, 6). Ввиду равенства всех вероятностей можно говорить о равномерном распределении случайной величины Х.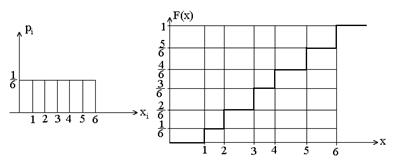

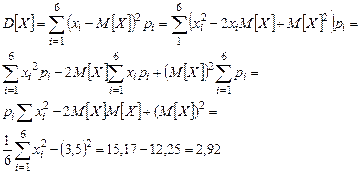
 .
.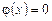 для всех значений, кроме интервала (a, b), на котором она постоянна. Постоянное значение обозначим через A. Тогда можно записать
для всех значений, кроме интервала (a, b), на котором она постоянна. Постоянное значение обозначим через A. Тогда можно записать
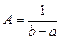 . Поэтому плотность равномерного распределения задается формулой
. Поэтому плотность равномерного распределения задается формулой
 .
.
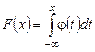 .
. . Тогда F (x) = 0.
. Тогда F (x) = 0.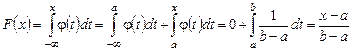 .
.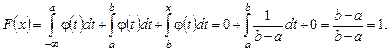
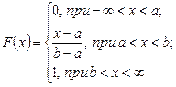
 .
.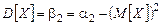 ;
; ;
;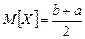 ;
; 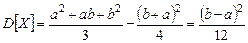 .
.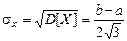 .
.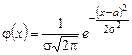 .
. . С ростом s величина максимального значения уменьшается, а так как площадь, ограниченная всей кривой и осью абсцисс, равна единице, то с ростом s кривая как бы растягивается вдоль оси ох и наоборот. Приведены графики у = j(х) при различных «а», но при одном и том же s. На другом – при а = 0, но различных s.
. С ростом s величина максимального значения уменьшается, а так как площадь, ограниченная всей кривой и осью абсцисс, равна единице, то с ростом s кривая как бы растягивается вдоль оси ох и наоборот. Приведены графики у = j(х) при различных «а», но при одном и том же s. На другом – при а = 0, но различных s. имеет место предел, когда j = 0 (по формуле). Разность (х
имеет место предел, когда j = 0 (по формуле). Разность (х 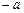 ) содержится в формуле в квадрате, т.е. график функции симметричен относительно прямой х = а.
) содержится в формуле в квадрате, т.е. график функции симметричен относительно прямой х = а.