
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Точечное оценивание параметров. РегрессионныйСодержание книги
Поиск на нашем сайте
И корреляционный анализ 2.1. Выборочный метод
Применение математической статистики к обработке наблюдений оказывается возможным благодаря использованию выборочного метода. Выборочный метод в самой общей форме выглядит следующим образом. Имеется некоторая большая совокупность объектов, называемая генеральной совокупностью. Из этой совокупности извлекается n объектов, которые образуют выборку; число n называется объемом выборки. Эти n объектов подвергаются детальному исследованию, по результатам которого требуется описать всю генеральную совокупность или какие–нибудь ее свойства, характеристики. Пример. Завод, выпускающий электролампы, должен контролировать свою продукцию, в частности, проверять долговечность ламп. Чтобы проверить срок службы лампы, нужно держать ее на испытательном стенде включенной до тех пор, пока она не перегорит. Если бы завод проверял все свои лампы, то его продукция не пошла бы дальше стенда. Из создавшегося положения находят простой выход: отбирают, скажем, одну лампу на тысячу и проверяют только отобранные лампы. В этом случае по долговечности ламп из выборки судят о долговечности всей генеральной совокупности выпускаемых заводом ламп.
Получается следующая схема производства наблюдений: имеется случайная величина Х и в результате n независимых испытаний получаются n ее допустимых значений. Если все допустимые значения случайной величины Х считать генеральной совокупностью, то полученные при наблюдениях n значений образуют выборку. По этой выборке мы и должны определить распределение случайной величины Х (т.е. распределение генеральной совокупности). При наблюдениях получают числа х 1, х 2,…, хn (элементы выборки). Их можно считать полной совокупностью значений некоторой конечнозначной случайной величины Хn и конечное распределение Хn называют выборочным (эмпирическим) распределением. Доказано: с вероятностью равной единице максимальная разность между функциями распределения случайных величин Х n и Х при n ® ¥ стремится к нулю. Практически это означает, что при достаточно большом объеме выборки функцию распределения генеральной совокупности можно приближенно заменять выборочной функцией распределения.
Среднее и дисперсия выборки
Пусть М [ Х ] – математическое ожидание случайной величины Х. Это число нам неизвестно. Мы проводим наблюдения и при большом объеме выборки n можно вместо М [ Х ] рассматривать математическое ожидание Хn. Погрешность при этом будет тем меньше, чем больше объем выборки n. Математическое ожидание выборки есть просто среднее арифметическое элементов выборки:
Будем называть средним выборки
где х i – варианта выборки; n i – частота варианты х i; n – объем выборки. Таким образом, в качестве истинного результата можно брать Дисперсия D [ Х ] приближенно равна дисперсии D [ Xn ].
т.е. D [ Х ]» D [ X n]. Это равенство было бы еще более надежным, если бы в формуле для D [ X n] вместо
которая является несмещенной оценкой дисперсии. Переход к несмещенной оценке S 2 важен в основном для малых выборок, ибо разница между S 2 и D [ X n] при больших n незаметна. Таким образом, среднее выборки
а несмещенная оценка дисперсии выборки
В практических вычислениях для дисперсии S 2 часто удобна формула
Величина S (корень квадратный из выборочной дисперсии) называется средним квадратическим отклонением выборки или выборочным стандартом. Почему в формуле дисперсии n заменили на n – 1? Это связано с тем, что входящая в формулу величина Каждая величина, зависящая от элементов выборки и участвующая в формуле выборочной дисперсии, называется связью. Эта разность показывает, какое количество элементов выборки можно произвольно изменять, не нарушая связей и называется числом степеней свободы. Таким образом, знаменатель выборочной дисперсии всегда равен разности между объемом выборки и числом связей, наложенных на эту выборку. 2.2. Связь между случайными величинами. Корреляция До сих пор изучали наблюдения над одной случайной величиной. Между тем для выяснения тех или иных причинно–следственных связей в окружающей природе необходимо вести одновременные наблюдения над целым рядом случайных величин, чтобы по полученным данным изучать взаимоотношения этих величин. Ограничимся пока двумя случайными величинами Х и У. В математическом анализе зависимость между двумя величинами выражается понятием функции у = f (x), где каждому допустимому значению одной переменной соответствует одно и только одно значение другой переменной. Такая зависимость называется функциональной, она обнаруживается с помощью строгих логических доказательств и не нуждается в опытной проверке. Если у = const при изменении х, то говорят, что у не зависит от х. Гораздо сложнее обстоит дело с понятием зависимости случайных величин: если при изменении х изменилось у, мы не можем сказать, является ли это изменение результатом зависимости у от х или это результат влияния случайных факторов. Здесь имеет место связь особого рода, при которой с изменением одной величины меняется распределение другой – такая связь называется стохастической. Выявление стохастической связи и оценка ее силы представляют задачу математической статистики. Рассматривая свойства дисперсии, мы указали, что дисперсия суммы двух независимых величин равна сумме дисперсий этих величин. Поэтому если для двух случайных величин Х и У окажется, что
то это служит верным признаком наличия зависимости между Х и У, т.е. корреляции. Из этого неравенства вытекает (доказано), что справедливо следующее неравенство:
где Корреляционный момент зависит от единиц измерения величин Х и У. Поэтому на практике чаще используется безразмерная величина, которая называется коэффициентом корреляции.
2.2.1. Свойства коэффициента корреляции 1. Коэффициент корреляции независимых или некоррелированных величин равен нулю. 2. Коэффициент корреляции не меняется от прибавления к Х или У каких–либо постоянных (неслучайных) слагаемых, от умножения их на положительные числа. 3. Если одну из случайных величин, не меняя другой, умножить на 4. Численно коэффициент корреляции заключен в пределах 5. Если r > 0, то величины Х и У с точностью до случайных погрешностей одновременно возрастают или убывают, если же r < 0, то с возрастанием одной величины другая убывает. Но это справедливо только для линейной зависимости У от Х. Т.е. зависимость между Х и У может быть строго функциональной (например, квадратичной) без следа случайности, а коэффициент корреляции все еще будет меньше 1. Таким образом, коэффициент корреляции есть показатель того, насколько связь между случайными величинами близка к строгой линейной зависимости. Он одинаково отмечает и слишком большую долю случайности, и слишком большую криволинейность этой связи. Если заранее, из общих соображений, можно предсказать линейную зависимость, то r является достаточным показателем тесноты связи между Х и У. Для случайных величин (большинство именно таких), подчиняющихся нормальному закону, равенство r = 0 означает одновременно и отсутствие всякой зависимости.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.183.77 (0.01 с.) |

 .
. . Если сгруппировать итоги наблюдений, то можно записать
. Если сгруппировать итоги наблюдений, то можно записать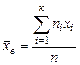 ,
, ,
, ,
, ,
, .
. .
. ,
,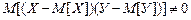 ,
, называют корреляционным моментом.
называют корреляционным моментом. .
. , то на
, то на 


