Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь входа и выхода. Способы построения моделей. Переходная функция и импульсная характеристика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Любой объект взаимодействует с внешней средой с помощью входов и выходов. Входы –это возможные воздействия на объект, выходы – это те сигналы, которые можно измерить. Например, для электродвигателя входами могут быть напряжение питания и нагрузка, а выходами– частота вращения вала, температура.Входы независимы, они «приходят» из внешней среды. При изменении информации навходе меняется внутреннее состояние объекта (так называют его изменяющиеся свойства) и,как следствие, выходы:
Это значит, что существует некоторое правило, по которому элемент преобразует вход x в вы- ход y. Это правило называется оператором. Запись y =U[x] означает, что выход y получен в результате применения оператора U ко входу x. Построить модель – это значит найти оператор, связывающий входы и выходы. С его помощью можно предсказать реакцию объекта на любой входной сигнал. Рассмотрим электродвигатель постоянного тока. Вход этого объекта – это напряжение питания (в вольтах), выход – частота вращения (в оборотах в секунду). Будем считать, что при напряжении 1 В частота вращения равна 1 об/сек, а при напряжении 2 В – 2 об/сек, то есть частота вращения равна по величине напряжению1. Легко вдеть, что действие такого оператораможно записать в видеU[x] = x. Теперь предположим, что этот же двигатель вращает колесо и в качестве выхода объекта мы выбрали число оборотов колеса относительно начального положения (в момент t = 0). В этом случае при равномерном вращении произведение x ⋅Δ t дает нам количество оборотов за время Δ t, то есть y (t) = x ⋅Δ t (здесь запись y (t) явно обозначает зависимость выхода от времени t). Можно ли считать, что этой формулой мы определили оператор U? Очевидно, что нет, потому что полученная зависимость справедлива только для постоянного входного сигнала. Если напряжение на входе x (t) меняется (все равно как!), угол поворота запишется в виде итеграла Оператор, который действует по такому правилу, называется оператором интгрирования. С помощью этого оператора можно, например, описать напонение пустого бака водой. Если сечение бака S (в м2) постоянно по всей его высоте, то уровень воды h определяется какинтеграл от потока воды q (в м3/с), деленный на S:
Обратный оператор- оператор дифференцирования– вычисляет производную:
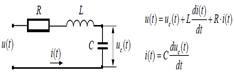
законы сохранения массы, энергии, импульса). Эти модели описываютвнутренние связи вобъекте и, как правило, наиболее точны.Рассмотрим RLC-цепочку, то есть последовательное соединение резистора с сопротивлением R (в омах), катушки индуктивности с индуктивностью L и конденсатора с емкостью C.Она может быть описана с помощью двух уравнений:
Первое уравнение означает, что разность потенциалов на концах RLC- цепочки равна сумме разностей потенциалов на всех промежуточных участках. Разность потенциалов R ⋅ i (t) на резисторе вычисляется по закону Ома, а на катушке – по формуле, приведенной в предыдущем параграфе. Второе уравнение описывает связь между напряжением и током для конденсатора. Вход этого объекта – напряжение u (t) на концах цепочки, а выход – разность потенциалов u (t) c на пластинах конденсатора. Второй способ – построение модели в результате наблюдение за объектом при различных входных сигналах (этим занимается теория идентификации). Объект рассматривается как «черный ящик», то есть, его внутреннее устройство неизвестно. Мы смотрим, как он реагирует на входные сигналы, и стараемся подстроить модель так, чтобы выходы модели и объекта совпадали как можно точнее при разнообразных входах. На практике часто используется смешанный способ: структура модели (вид уравнения, связывающего вход и выход) определяется из теории, а коэффициенты находят опытным путем. Например, общий вид уравнений движения корабля хорошо известен, однако в этих уравнениях есть коэффициенты, которые зависят от многих факторов (формы корпуса, шероховатости поверхности и т.п.), так что их крайне сложно (или невозможно) найти теоретически. В этом случае для определения неизвестных коэффициентов строят масштабные модели и испытывают их в бассейнах по специальным методикам. В авиастроении для тех же целей используют аэродинамические трубы. Для любого объекта управления можно построить множество различных моделей, кото- рые будут учитывать (или не учитывать) те или иные факторы. Обычно на первом этапе стараются описать объект как можно более подробно, составить детальную модель. Однако при этом будет трудно теоретически рассчитать закон управления, который отвечает заданным требованиям к системе. Даже если мы сможем его рассчитать, он может оказаться слишком сложным для реализации или очень дорогим. С другой стороны, можно упростить модель объекта, отбросив некоторые «детали», кото- рые кажутся разработчику маловажными. Для упрощенной модели закон управления также получается проще, и с его помощью часто можно добиться желаемого результата. Однако в этом случае нет гарантии, что он будет так же хорошо управлять полной моделью (и реальным объектом). Обычно используется компромиссный вариант. Начинают с простых моделей, стараясь спроектировать регулятор так, чтобы он «подходил» и для сложной модели. Это свойство называют робастностью (грубостью) регулятора (или системы), оно означает нечувствительность к ошибкам моделирования. Затем проверяют работу построенного закона управления на полной модели или на реальном объекте. Если получен отрицательный результат (простой регулятор «не работает»), усложняют модель, вводя в нее дополнительные подробности. И все начинается сначала. Понятие передаточной функции. Преобразования Лапласа. Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал. В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях. Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими. Прямое преобразование Лапласа Преобразованием Лапласа функции вещественной переменной
Правая часть этого выражения называется интегралом Лапласа. Обратное преобразование Лапласа Обратным преобразованием Лапласа функции комплексного переменного
где Двустороннее преобразование Лапласа Основная статья: Двустороннее преобразование Лапласа Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции Двустороннее преобразование Лапласа определяется следующим образом:
Дискретное преобразование Лапласа Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций. Различают · Пусть Тогда применяя преобразование Лапласа получим:
· Основная статья: Z-преобразование Если применить следующую замену переменных: z = esT, получим Z -преобразование:
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |


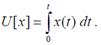
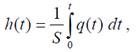
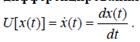
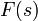 комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией 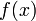 вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.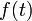 , называется функция
, называется функция 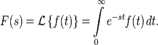
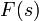 , называется функция
, называется функция 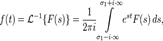
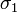 — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.
— некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.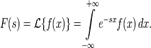
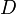 -преобразование и
-преобразование и 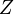 -преобразование.
-преобразование.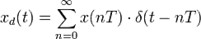 — решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени
— решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени 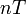 , где
, где 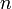 — целое число, а
— целое число, а  — период дискретизации.
— период дискретизации.