
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Степенная функция с натуральным показателнм.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Степенной функцией с натуральным показателем При Свойства степенной функции: 1). Область определения функции: 2). Для любых 3). Для любых Степенные функции имеют смысл и при
Пример степенных функций
5. Функция Свойства функции корня: При четном 1). Область определения: луч 2). Функция 3). Функция 4). График функции
При нечетном 1). Область определения функции 2). Функция 3). Функция 4). График функции
Показательная функция Функция вида Свойства показательной функции: 1). Область определения функции: 2). Область значений: 3). Если 4). При При Примеры показательных функций
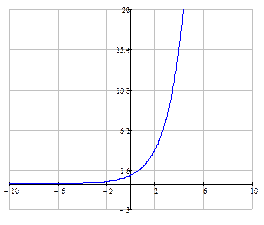
Логарифмическая функция Логарифмической функцией называется функция вида Логарифмическая функция является функцией, обратной показательной. Свойства логарифмической функции: 1). Область определения функции: 2). Область значений: 3). Функция не является ни четной, ни нечетной. 4). Функция непрерывна и не имеет ни наибольшего, ни наименьшего значений. 5). При 6). При
Предел функции. Пусть функция Обозначение: Запишем это определение коротко:
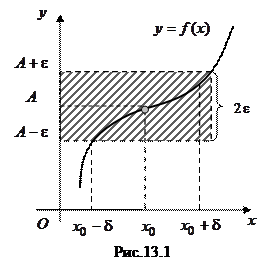
Геометрический смысл предела функции поможет понять рис. 13.1. Для любой Пусть функция Обозначение: Запишем определение предела функции коротко:
что для всех точек этой окрестности соответствующие значения функции Если рассматривается поведение функции при Пусть Запишем определение коротко:
Если функция Пусть функция Обозначение: Коротко определение:
Геометрический смысл определения: для любой окрестности На экзамене достаточно привести классическое определение (1 случай). Но как выглядит определение для других случаев знать надо (это всегдашний дополнительный вопрос!)
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 905; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

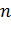 называется функция
называется функция  .
.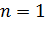 получаем прямую пропорциональность:
получаем прямую пропорциональность:  ; при
; при  – квадратную параболу; при
– квадратную параболу; при  – обратную пропорциональностьилигиперболу.
– обратную пропорциональностьилигиперболу.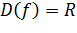
 .
.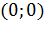 .
. , но их графики имеют различный вид в зависимости от того, является ли
, но их графики имеют различный вид в зависимости от того, является ли 






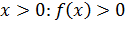 ; при
; при 
 Функция убывает на
Функция убывает на 

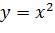 (парабола)
(парабола)
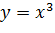 (кубическая парабола)
(кубическая парабола)

 .
. обладает теми же свойствами, что и функция
обладает теми же свойствами, что и функция  :
: . Это следует из, того что выражение
. Это следует из, того что выражение  определено лишь при
определено лишь при  .
.
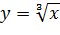 :
:
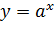 , при
, при 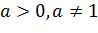 называется показательной функцией с основанием
называется показательной функцией с основанием 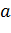 .
.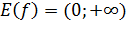 .
.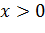 , то
, то 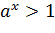 и если
и если 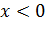 , то
, то 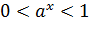 .
. функция строго монотонно возрастает на всей числовой прямой.
функция строго монотонно возрастает на всей числовой прямой.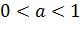 функция строго монотонно убывает на всей числовой прямой.
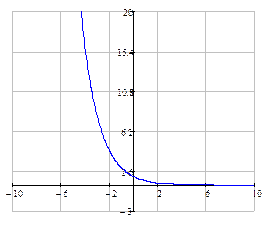
функция строго монотонно убывает на всей числовой прямой.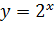 и
и 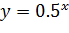 :
:
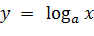 , при
, при  .
.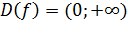
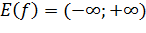 .
. функция строго возрастает, а при
функция строго возрастает, а при  строго убывает.
строго убывает.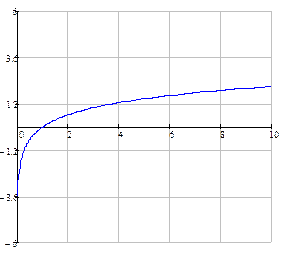
 Пример логарифмических функций
Пример логарифмических функций  и
и  :
: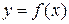 определена в некоторой окрестности точки
определена в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  .
.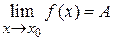 .
.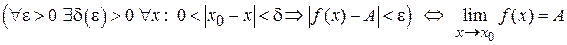 .
. Квантор всеобщности
Квантор всеобщности 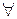 читается: «для всех». Квантор существования
читается: «для всех». Квантор существования  заменяет слово «существует». Запись
заменяет слово «существует». Запись 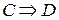 означает, что «из
означает, что «из  следует
следует  ». А
». А 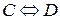 указывает на эквивалентность высказываний
указывает на эквивалентность высказываний 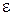 -окрестности точки
-окрестности точки  (ось
(ось  ) найдется такая
) найдется такая 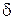 -окрестность точки
-окрестность точки 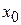 (ось
(ось  ), что для всех точек этой окрестности, кроме, быть может,
), что для всех точек этой окрестности, кроме, быть может, 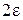 , ограниченной прямыми
, ограниченной прямыми 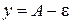 ,
, 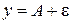 . Величина
. Величина 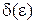 .
.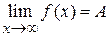 .
. .
. Геометрический смысл этого определения: для любой e‑окрестности точки
Геометрический смысл этого определения: для любой e‑окрестности точки 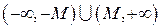 (ось
(ось 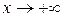 или при
или при  , то пишут
, то пишут 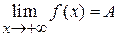 и, соответственно,
и, соответственно, 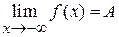 .
.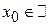 . Определение. Функция
. Определение. Функция  (включая бесконечность), если
(включая бесконечность), если  .
.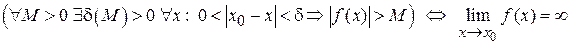 .
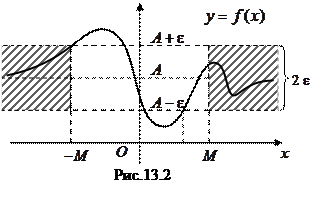
.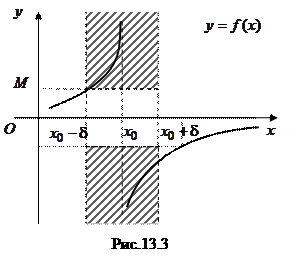 Геометрический смысл определения: для любой окрестности бесконечно удаленной точки
Геометрический смысл определения: для любой окрестности бесконечно удаленной точки 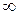 , т. е. точки графика лежат выше прямой
, т. е. точки графика лежат выше прямой  и ниже прямой
и ниже прямой 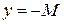 (рис. 13.3).
(рис. 13.3). , а если, принимая лишь отрицательные значения, то пишут
, а если, принимая лишь отрицательные значения, то пишут 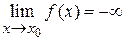 .
.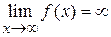 .
.
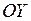 найдется такая окрестность
найдется такая окрестность 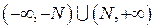 бесконечно удаленной точки оси
бесконечно удаленной точки оси 


