
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многочлены и действия над ними.Содержание книги
Поиск на нашем сайте Определение. Для действительной переменной x функция вида Определение. Многочлен ‑ это сумма одночленов, т.е. функция вида
Многочлен тождественно равен 0 тогда и только тогда, когда все его коэффициенты равны 0. Если в записи многочлена нет какой-либо степени неизвестного, это значит, что коэффициент при этой степени равен 0. На множестве многочленов определены следующие действия: 1. Сложение. 2. Умножение. 3. Деление с остатком. Разделить Теорема (о делении с остатком) [Для любых многочленов
Для практического нахождения частного и остатка существует метод деления «уголком». Пример 11.1. Выполнить «уголком» деление с остатком:
Находим частное от деления старшего члена делимого на старший член делителя (
x Умножаем делитель на результат деления и записываем под делимым:
Вычитаем из делимого результат умножения:
Проверяем степень получившегося в результате вычитания многочлена. Если она меньше степени делителя, то процесс деления закончен, и полученный многочлен является остатком. В противном случае деление продолжается аналогично описанному ранее:
Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате:
Ответ:
Определение. Корнем многочлена Теорема Безу. Для любой функции где Следствие. Число Удобной для деления на многочлены вида (
Пример 11.2. Разделить Решение. Воспользуемся схемой Горнера. Нарисуем таблицу и выполним расчеты.
Итак, Ответ: Здесь примеры приведены для того, чтобы вы вспомнили, как это делается. Рассказывать их не нужно.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 , где a и x –действительные числа, а n – натуральное число или 0 (по-другому это можно записать как
, где a и x –действительные числа, а n – натуральное число или 0 (по-другому это можно записать как  ), называется одночленом с действительным коэффициентом.
), называется одночленом с действительным коэффициентом. .
. называется старшим коэффициентом и
называется старшим коэффициентом и  ,
,  ‑ свободным членом, n ‑ степенью многочлена.
‑ свободным членом, n ‑ степенью многочлена. на
на  ‑ значит записать
‑ значит записать  , или
, или  . Последняя запись аналогична записи для чисел:
. Последняя запись аналогична записи для чисел:  , или 17 = 5 × 3 + 2.
, или 17 = 5 × 3 + 2. существуют, и притом единственные, многочлены
существуют, и притом единственные, многочлены  и
и 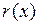 , такие, что
, такие, что . (11.1)
. (11.1)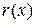 меньше степени
меньше степени  ,
,  ‑ неполное частное,
‑ неполное частное,  на
на  .
.
 Решение. Запишем делимое
Решение. Запишем делимое  ) и записываем результат в графу частного:
) и записываем результат в графу частного:




 x
x







 ‑ 4 x
‑ 4 x , или
, или
 .
. называется число
называется число  такое что
такое что  .
. верно равенство:
верно равенство:
 .
. без остатка.
без остатка. ) является схема Горнера. Рисуем таблицу, в первой строке которой записываем все коэффициенты
) является схема Горнера. Рисуем таблицу, в первой строке которой записываем все коэффициенты 









 ‑ коэффициенты неполного частного от деления
‑ коэффициенты неполного частного от деления  ‑ остаток от деления, который по теореме Безу равен
‑ остаток от деления, который по теореме Безу равен  . Если
. Если  = 0, то говорят, что
= 0, то говорят, что  на
на  .
.



 , где
, где  ‑ коэффициенты неполного частного. Следовательно,
‑ коэффициенты неполного частного. Следовательно,  .
. .
.


