
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели законов распределения вероятностей, наиболее употребляемые в социально-экономических приложениях.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Случайная величина непрерывного типа называется распределенной равномерно на отрезке Для равномерно распределенной случайной величины
Равномерное распределение используется при решении практических задач, в которых заранее известно, что возможные значения случайной величины лежат в некотором интервале, и все значения в пределах этого интервала одинаково вероятны. Для случайной величины, распределенной равномерно на отрезке Непрерывная случайная величина ξ называется распределенной по показательному (экспоненциальному) закону, если ее плотность распределения задается формулой:
где Показательное распределение часто встречается в теории массового обслуживания и в теории надежности. Величина ξ, распределенная по показательному закону, хорошо описывает время ожидания при техническом обслуживании и длительность телефонных разговоров, регистрируемых на телефонной станции, и срок службы радиоэлектронной или другой аппаратуры. Для случайной величины, распределенной по показательному закону с параметром Случайная величина ξ называется распределенной по нормальному (гауссовскому) закону с параметрами а и
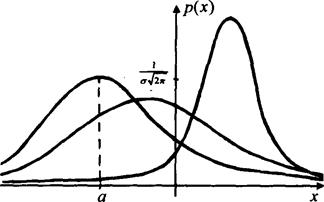
где Теоретические исследования показали, что большинство встречающихся на практике случайных величин имеет нормальный закон распределения. По этому закону распределяется скорость газовых молекул, вес новорожденных, размер одежды и обуви населения страны и много других случайных событий физической и биологической природы. Впервые эту закономерность заметил и теоретически обосновал А. Муавр. Величина, распределенная по нормальному закону, всегда имеет бесчисленное множество возможных значений, поэтому ее удобно изображать графически. Вероятность того, что случайная величина примет значение из интервала На рисунке 29.1 изображено несколько кривых плотности распределения случайной величины, заданной по нормальному закону. Несмотря на все различия, эти кривые обладают следующими общими чертами. 1. Все кривые имеют одну точку максимума, при удалении от которой вправо и влево кривые убывают. Максимум 2. Кривые симметричны относительно вертикальной прямой, проведенной через наивысшую точку. 3. Площадь подграфика каждой кривой равна 1. Это следует из свойства
Рис. 29.1. Для случайной величины, распределенной по нормальному закону с параметрами а и Вероятность того, что нормально распределенная величина примет значение из интервала
где Часто в задачах требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины ξ от своего математического ожидания по абсолютной величине не превосходит некоторого значения Применяя формулу (29.4), имеем:
В заключение приведем одно важное следствие из формулы (29.5). Положим в этой формуле
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

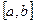 , если ее плотность распределения постоянна на этом отрезке и равна нулю вне отрезка.
, если ее плотность распределения постоянна на этом отрезке и равна нулю вне отрезка.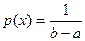 при
при 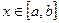 . (29.1)
. (29.1)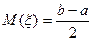 ,
, 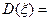
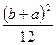 .
.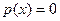 при
при  и
и 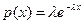 при
при 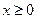 , (29.2)
, (29.2)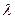 - постоянная положительная величина, которая называется параметром распределения.
- постоянная положительная величина, которая называется параметром распределения.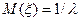 ,
,  . Среднее квадратическое отклонение -
. Среднее квадратическое отклонение - 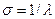 .
. (
( ), если плотность распределения вероятностей имеет вид
), если плотность распределения вероятностей имеет вид , (29.3)
, (29.3)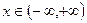 .
.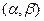 , равна площади под графиком функции
, равна площади под графиком функции  на этом интервале (геометрический смысл определенного интеграла).
на этом интервале (геометрический смысл определенного интеграла).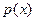 достигается при
достигается при 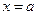 и равен
и равен 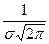 .
.
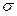 , математическое ожидание и дисперсия вычисляются по формулам:
, математическое ожидание и дисперсия вычисляются по формулам: 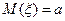 ,
,  . Среднее квадратическое отклонение равно
. Среднее квадратическое отклонение равно 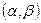 , равна
, равна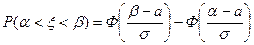 , (29.4)
, (29.4) есть функция Лапласа.
есть функция Лапласа.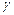 , т.е. вычислить вероятность
, т.е. вычислить вероятность  .
.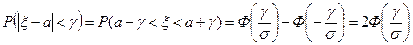 . (29.5)
. (29.5)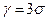 . Тогда
. Тогда  , т.е. вероятность того, что абсолютная величина отклонения ξ от своего математического ожидания не превысит
, т.е. вероятность того, что абсолютная величина отклонения ξ от своего математического ожидания не превысит 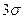 , равна 99,73%. Практически такое событие можно считать достоверным. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания практически не превосходит утроенного среднего квадратического отклонения.
, равна 99,73%. Практически такое событие можно считать достоверным. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания практически не превосходит утроенного среднего квадратического отклонения.


