
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные величины и способы их описания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение. Случайной величиной называется величина, которая принимает в результате опыта или эксперимента одно из множества возможных значений. Для того, чтобы охарактеризовать случайную величину, необходимо знать те значения, которые она может принимать. Также надо знать и как часто, т.е. с какой вероятностью, она принимает эти значения. Разнообразие случайных величин весьма велико. Число принимаемых значений может быть конечным или бесконечным, значения могут быть расположены на числовой оси дискретно или заполнять некоторые интервалы целиком. В зависимости от этого свойства случайные величины принято разделять на дискретные и непрерывные. Определение. Дискретной называется случайная величина, которая может принимать конечное или счетное множество различных значений. (Напомним, что счетным называется множество, все элементы которого можно поставить во взаимно-однозначное соответствие с числами натурального ряда, т.е. перенумеровать.) Рассмотрим сначала случайные величины, которые могут принимать лишь конечное число различных значений. Пусть возможными исходами некоторого эксперимента являются события Введем некоторую числовую функцию x, которая ставит в соответствие событиям числа: Этот факт может быть записан следующим образом: Теперь вместо того, чтобы говорить «события Набор Случайную величину x удобно задавать в виде таблицы:
Эта таблица называется законом распределения величины x. Если случайная величина x может принимать несчетное множество значений, которые сплошь заполняют некоторые промежутки числовой оси, то такую величину невозможно описать таблицей. Ее принято задавать с помощью специальной функции – функции распределения, которая дает полную информацию о поведении случайной величины. Функцией распределения вероятностей случайной величины x называется функция F, определенная равенством
Функция распределения F случайной величины x в точке x равна вероятности того, что x принимает значение, меньшее x. Очевидно, что для дискретной случайной величиныx, которая принимает значения Определение. Если для случайной величины x существует неотрицательная функция
то x называется непрерывной случайной величиной, а функция
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1009; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 ,
,  , …
, …  , которые образуют полную группу попарно несовместных событий. Пусть
, которые образуют полную группу попарно несовместных событий. Пусть  (т.е. вероятность появления события Аi в результате эксперимента равна
(т.е. вероятность появления события Аi в результате эксперимента равна  ). Заметим, что
). Заметим, что  .
. ,
,  , …,
, …,  . Таким образом, мы определили значения, которые может принимать случайная величина x: если наступило событие Аi, то случайная величина принимает значение xi
. Таким образом, мы определили значения, которые может принимать случайная величина x: если наступило событие Аi, то случайная величина принимает значение xi  .
. (вероятность того, что случайная величина принимает значение xi,равна
(вероятность того, что случайная величина принимает значение xi,равна  », можем сказать «задана случайная величина x, которая принимает значения
», можем сказать «задана случайная величина x, которая принимает значения  ,
,  , …
, …  с вероятностями
с вероятностями  ,
,  , …
, …  ».
». х2
х2
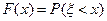 .
. определена для любых случайных величин при
определена для любых случайных величин при  , возрастает с ростом x и полностью описывает случайную величину.
, возрастает с ростом x и полностью описывает случайную величину. . Эта функция является разрывной и возрастает скачками при тех значениях x, которые являются возможными значениями величиныx.
. Эта функция является разрывной и возрастает скачками при тех значениях x, которые являются возможными значениями величиныx.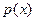 , удовлетворяющая при любых x равенству
, удовлетворяющая при любых x равенству ,
,


