
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Функции случайного аргументаСодержание книги
Поиск на нашем сайте
Лекция 13 13.1. Теорема Бернулли (закон больших чисел).
Если в каждом из n независимых испытаний вероятность p появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
Если случайные величины попарно независимы и дисперсии их ограничены, то можно ли применить к рассматриваемым величинам теорему Чебышева Оба условия выполняются. Действительно, попарная независимость величин
** Известно, что произведение двух сомножителей, сумма которых есть величина постоянная, имеет наибольшее значение при равенстве сомножителей. Здесь сумма
Применяя теорему Чебышева (частный случай) к рассматриваемым величинам, имеем
Приняв во внимание, что математическое ожидание а каждой из величин Х{ (т. е. математическое ожидание числа появлений события в одном испытании) равно вероятности р наступления события, получим
Остается показать, что дробь
Учитывая это равенство, окончательно получим
Замечание. Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р, другими словами из теоремы Бернулли не вытекает равенство
В теореме речь идет лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Таким образом, сходимость относительной частоты Теорема Бернулли утверждает, что при Устойчивость нормального распределения Закон распределения вероятности называют устойчивым, если композиция таких законов есть тот же закон, отличающийся параметрами. Нормальный закон обладает свойством устойчивости. Композиция нормальных законов имеет нормальное распределение, при этом математическое ожидание и дисперсия композиции равна суммам математических ожиданий и дисперсий слагаемых.
Упражнения 2.3.1. Закон распределения случайной величины X имеет вид:
Найти закон распределения случайной величины 2.3.2. Число X неисправностей на участке высоковольтной линии в течение года имеет распределение Пуассона с параметром a ( 2.3.3. СВДТ X имеет пуассоновское распределение 2.3.4. Задана плотность распределения 1) 2.3.5. Задана плотность распределения 1)
Ответы к упражнениям 2.3.1.
2.3.2.
2.3.3. 1. 2.3.4. 1) 2.3.5. 1) 2)
Задача композиции Очень часто встречается функциональная зависимость вида т.е. возникает задача определения закона распределения суммы компонент случайного вектора 1. Пусть X и Y – СВДТ с известным законом совместного распределения где суммирование распространяется на все значения индексов i и j, для которых выполняется условие Пример 11. Закон распределения случайного вектора
Составив закон распределения случайной величины Решение. Найдем вначале значения функции Значит, случайная величина Z имеет пять возможных значений: Вероятность возможного значения
Тогда найдем функцию распределения Вычислим теперь Ответ: 2. Пусть X и Y – СВНТ с известной плотностью совместного распределения компонент Особо важным для практики представляется частный случай, когда X и Y – независимые случайные величины, а 1. Пусть X и Y – независимые СВДТ, тогда или
Пример 2.3.12. Рассматривается случайная величина Z – суммарное число «успехов» в двух независимых опытах с одной и той же вероятностью «успеха» p в каждом опыте. Найти закон распределения случайной величины Z и составить ее функцию распределения. Решение. Пусть X – количество успехов в первом опыте, а Y – количество успехов во втором опыте. По условию задачи X и Y независимы. Тогда с вероятностями соответственно. Тогда ряд распределения примет вид
Составим теперь функцию распределения случайной величины Ответ: 2. Пусть X и Y – независимые СВНТ, Этот интеграл можно вычислять как повторный: Дифференцируя по z, получаем: Две последние формулы носят название формул свертки. С помощью этих формул можно выразить функцию распределения
Пример 2.3.13. Пусть случайные величины X и Y – независимы, Составить функцию распределения и функцию плотности суммы Решение. Применяя формулу свертки, имеем т.к. производная интеграла по переменной z равна значению подынтегральной функции от верхнего предела, умноженного на производную по z от верхнего предела, минус значение подынтегральной функции от нижнего предела, умноженного на производную по z от нижнего предела. Отсюда следует существование плотности Ответ:
Пример 2.3.14. Случайные величины X и Y независимы и равномерно распределены на отрезке Решение. 1 способ. По условию возможные значения X определяются неравенством
а б Рис. 2.3.2. По определению функции распределения Неравенству С другой стороны, т.к. случайные величины X и Y независимы, то где область G – часть квадрата ABCD, которая расположена ниже прямой Если Если поэтому Если Найдем теперь плотность распределения График функции плотности
Рис. 2.3.3. 2 способ. Учтем, что в данном случае подынтегральное выражение в формуле свертки Рассматривая два случая взаимного расположения отрезков, на которых плотности одновременно отличны от нуля (рис. 2.3.4), получим:
Рис. 2.3.4. Ответ: Определение. Закон распределения W определенного вида называется композиционно устойчивым, если из того, что две независимые случайные величины X и Y подчиняются закону распределения данного типа, следует, что их сумма Рассмотрим примеры композиционно устойчивых распределений.
Пример 2.3.15. Найти закон распределения суммы двух независимых случайных величин X и Y, распределенных по закону Пуассона: Решение. Найдем вероятность события Следовательно, случайная величина Ответ: Пример 2.3.16. Найти закон распределения суммы двух независимых случайных величин X и Y, распределенных по биномиальному закону: Решение. Представим случайную величину X в виде: где Ряд распределения случайной величины
Аналогичное представление сделаем и для случайной величины Y: где Ряд распределения случайной величины
Следовательно, где каждое из слагаемых является индикаторной случайной величиной распределенной по одному и тому же закону:
Всего слагаемых – Ответ: Замечание 1. Если вероятности p в различных сериях опытов (первая серия опытов описывается случайной величиной X, а вторая серия – случайной величиной Y) будут различны, то в результате сложения двух независимых случайных величин X и Y, распределенных по биномиальным законам, получится случайная величина Z, распределенная не по биномиальному закону. Замечание 2. Примеры 2.3.15 и 2.3.16 легко обобщаются на произвольное число слагаемых (Проделайте выкладки самостоятельно!).
Пример 2.3.17. Случайные величины X и Y независимы и нормально распределены: Решение. Пользуясь формулой свертки Из курса интегрального исчисления известно, что В данном случае Таким образом, из структуры плотности следует, что случайная величина Ответ:
Упражнения 2.3.6. Независимые случайные величины имеют биномиальное распределение 2.3.7. Законы распределения случайных величин X и Y имеют вид:
Найти распределение случайной величины 2.3.8. Законы распределения случайных величин X и Y имеют вид:
Найти распределение случайной величины 2.3.9. Независимые случайные величины имеют показательное распределение 2.3.10. Независимые случайные величины имеют равномерное распределение 2.3.11. Независимые случайные величины имеют равномерное распределение 2.3.12. Случайные величины X и Y независимы и нормально распределены:
Ответы к упражнениям 2.3.6. 0,84. 2.3.7.
2.3.8.
2.3.9. 2.3.10. 2.3.11. 2.3.12. Упражнения 2.3.13. СВНТ X имеет плотность вероятности Найти 2.3.14. Плотность вероятности случайной величины X имеет следующий вид: Найти 2.3.15. Пусть существуют дисперсии случайных величин X и Y такие, что 2.3.16. Известно, что случайная величина 2.3.17. Известно, что случайная величина 2.3.18. Известно, что случайные величины 2.3.19. Подбрасывают три игральные кости. Рассматриваются случайные величины: X – количество костей, на которых выпало шесть очков, Y – количество костей, на которых выпало пять очков. Найти 2.3.20. Предприятие имеет две поточные линии по сборке некоторой продукции. Технологические процессы на линиях связаны между собой. Рассматривая в качестве случайной величины X – количество единиц продукции, собранной за день на первой линии, а Y – на второй линии, совместное распределение этих величин можно задать с помощью таблицы:
Составить закон распределения случайной величины
Ответы к упражнениям 2.3.13. 2.3.14. 2.3.15. 0. 2.3.16. 0. 2.3.17. 0. 2.3.18. 2.3.19. 2.3.20.
Характеристическая функция Если Определение. Характеристической функцией случайной величины X называется комплекснозначная функция где В частности, Замечание 1. По характеристической функции Замечание 2. Характеристическая функция представляет собой
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.008 с.) |

 .
. Обозначим через
Обозначим через  дискретную случайную величину — число появлений события в первом испытании, через
дискретную случайную величину — число появлений события в первом испытании, через  — во втором,-..., Хп —в n-м испытании- Ясно, что каждая из величин может принять лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие не появилось) с вероятностью q=1-p.
— во втором,-..., Хп —в n-м испытании- Ясно, что каждая из величин может принять лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие не появилось) с вероятностью q=1-p. следует из того, что испытания независимы. Дисперсия любой величины
следует из того, что испытания независимы. Дисперсия любой величины  (i = 1,2,...,n) равна произведению n pq= pq (n=1); так как p+q=1, топроизведение pq не превышает 1/4 и, следовательно, дисперсии всех величин ограничены, например, числом С = 1/4.
(i = 1,2,...,n) равна произведению n pq= pq (n=1); так как p+q=1, топроизведение pq не превышает 1/4 и, следовательно, дисперсии всех величин ограничены, например, числом С = 1/4. , т. е. постоянна, поэтому при
, т. е. постоянна, поэтому при  произведение имеет наибольшее значение
произведение имеет наибольшее значение 


 равна относительной частоте т/п появлений события А виспытаниях. Действительно, каждая из величин
равна относительной частоте т/п появлений события А виспытаниях. Действительно, каждая из величин  равна числу явлений события в п испытаниях, а значит,
равна числу явлений события в п испытаниях, а значит,

 .
. к вероятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если
к вероятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если  к р как пределу в смысле обычного анализа, то начиная с некоторого n = N и для всех последующих значений n неуклонно выполняется неравенство
к р как пределу в смысле обычного анализа, то начиная с некоторого n = N и для всех последующих значений n неуклонно выполняется неравенство  ; если же
; если же 


 .
. ). Общий материальный ущерб Y от этих неисправностей пропорционален квадрату их числа:
). Общий материальный ущерб Y от этих неисправностей пропорционален квадрату их числа:  , где
, где  – неслучайная величина. Найти закон распределения этого ущерба.
– неслучайная величина. Найти закон распределения этого ущерба. , а
, а  . Вычислить
. Вычислить  .
. случайной величины X, возможные значения которой заключены в интервале
случайной величины X, возможные значения которой заключены в интервале  . Найти плотность распределения
. Найти плотность распределения  случайной величины Y, если:
случайной величины Y, если: ; 2)
; 2)  ; 3)
; 3)  .
. . Найти плотность распределения
. Найти плотность распределения  ; 2)
; 2)  ; 3)
; 3)  .
.





 ,
,  ; 2)
; 2)  ,
,  ; 3)
; 3)  ,
,  ,
,  ;
; ,
,  ; 3)
; 3)  ,
,  .
. ,
, по известному закону совместного распределения его компонент X и Y. Покажем, как эта задача решается в двух случаях, когда компоненты X и Y: 1) СВДТ; 2) СВНТ.
по известному закону совместного распределения его компонент X и Y. Покажем, как эта задача решается в двух случаях, когда компоненты X и Y: 1) СВДТ; 2) СВНТ. , где
, где  – множество возможных значений компоненты X,
– множество возможных значений компоненты X,  – множество возможных значений компоненты Y. Тогда закон распределения
– множество возможных значений компоненты Y. Тогда закон распределения  записывается в виде
записывается в виде ,
, . Затем, построив ряд распределения случайной величины Z (исключая все те значения
. Затем, построив ряд распределения случайной величины Z (исключая все те значения  , вероятность которых равна нулю), можно составить функцию распределения
, вероятность которых равна нулю), можно составить функцию распределения  .
. задан таблицей:
задан таблицей:

 , найти функцию распределения
, найти функцию распределения  ,
,  .
. :
: ,
,  ,
, 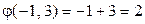 ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  ,
,  .
. и
и  , т.е.
, т.е.  . Исключим значения
. Исключим значения 

 ,
,  .
.
 ,
,  .
. , тогда
, тогда .
.
 .
. ,
,  ,
,  ,
,  , qp, pq,
, qp, pq, 
 :
:
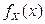 и
и  – их плотности. Плотность совместного распределения равна
– их плотности. Плотность совместного распределения равна  . Функция распределения суммы
. Функция распределения суммы  равна
равна .
.
 .
. и плотность
и плотность  суммы независимых случайных величин через плотности и функции распределения слагаемых. Отметим, что в силу симметрии переменных x и y формулы свертки можно записать следующим образом:
суммы независимых случайных величин через плотности и функции распределения слагаемых. Отметим, что в силу симметрии переменных x и y формулы свертки можно записать следующим образом: ,
, .
. – функция распределения Х, а Y имеет плотность
– функция распределения Х, а Y имеет плотность
 ,
, .
. ,
,  :
:  ,
,  . Найти плотность вероятности случайной величины
. Найти плотность вероятности случайной величины  , возможные значения Y – неравенством
, возможные значения Y – неравенством  . Отсюда следует, что возможные случайные точки
. Отсюда следует, что возможные случайные точки  расположены в квадрате ABCD.
расположены в квадрате ABCD.

 .
. удовлетворяют те точки
удовлетворяют те точки  плоскости xOy, которые лежат ниже прямой
плоскости xOy, которые лежат ниже прямой  (эта прямая отсекает на осях Ox и Oy отрезки, равные z). Если же брать только возможные значения x и y, то неравенство
(эта прямая отсекает на осях Ox и Oy отрезки, равные z). Если же брать только возможные значения x и y, то неравенство  ,
, – площадь G. Очевидно, что величина площади
– площадь G. Очевидно, что величина площади  , то
, то  , поэтому
, поэтому  . Если
. Если  (рис. 2.3.2 а), то
(рис. 2.3.2 а), то  , поэтому
, поэтому  .
. (рис. 2.3.2 б), то
(рис. 2.3.2 б), то ,
, .
. ,
,  , поэтому
, поэтому  .
. , продифференцировав
, продифференцировав  по z:
по z:

 отлично от нуля лишь в случае, когда
отлично от нуля лишь в случае, когда  принадлежит отрезку
принадлежит отрезку  , а именно:
, а именно: , если
, если  , если
, если 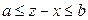 .
. , если
, если  , если
, если 
 ,
,  .
. , где
, где  :
:
 .
. . Значит, распределение Пуассона композиционно устойчиво.
. Значит, распределение Пуассона композиционно устойчиво. .
. ,
,  .
. ,
, (
(  ) – индикатор события A в i -м опыте:
) – индикатор события A в i -м опыте:


 ,
, (
(  ) – индикатор события A в j -м опыте:
) – индикатор события A в j -м опыте: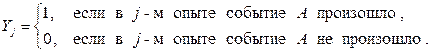
 ,
, . Отсюда следует, что случайная величина
. Отсюда следует, что случайная величина  .
. ,
,  . Найти плотность вероятности случайной величины
. Найти плотность вероятности случайной величины  .
. .
. ,
,  ,
,  .
. , где
, где  ,
,  . Значит, нормальное распределение композиционно устойчиво.
. Значит, нормальное распределение композиционно устойчиво. ,
,  . Вычислить значение
. Вычислить значение  , если
, если  ,
,  . Найти плотность распределения случайной величины
. Найти плотность распределения случайной величины  ,
,  . Найти функцию распределения и плотность распределения случайной величины
. Найти функцию распределения и плотность распределения случайной величины 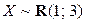 ,
,  . Найти функцию распределения и плотность распределения случайной величины
. Найти функцию распределения и плотность распределения случайной величины 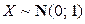 ,
,  . Найти плотность вероятности случайной величины
. Найти плотность вероятности случайной величины 




 , т.е.
, т.е.  .
. .
. и
и  .
.
 и
и  .
. . Чему равна ковариация случайных величин
. Чему равна ковариация случайных величин  и
и  ?
? ,
,  ,
,  . Найти
. Найти  .
. . Пусть
. Пусть  . Найти
. Найти  . Вычислить
. Вычислить  .
.
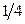

 и
и  .
. ,
,  .
. ,
,  .
. .
. ,
,  .
.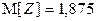 ,
,  ; закон распределения Z:
; закон распределения Z: – комплекснозначная случайная величина, где X и Y – действительные случайные величины, то
– комплекснозначная случайная величина, где X и Y – действительные случайные величины, то .
. ,
, ,
,  .
. , если X – СВДТ;
, если X – СВДТ; , если X – СВНТ.
, если X – СВНТ. однозначно восстанавливается функция распределения
однозначно восстанавливается функция распределения  .
.


