
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции одномерного случайного аргументаСодержание книги
Поиск на нашем сайте
Пусть на вероятностном пространстве ( 1. Пусть случайная величина X является дискретной. Функция Однако, как правило, удобнее вначале составить ряд распределения случайной величины
Пример 1. Закон распределения случайной величины X имеет вид:
Рассмотрим две числовые функции Решение. 1) Найдем возможные значения случайной величины Y= Тогда ряд распределения случайной величины Y имеет вид:
Составим теперь функцию распределения случайной величины 2) Найдем вначале значения функции Значит, случайная величина Z имеет три возможных значения: Вероятность возможного значения
Составим теперь функцию распределения случайной величины Ответ: 1) 2. Пусть случайная величина X является непрерывной. Рассмотрим вначале случайную величину где Если же В частности, если функция Пример 2. Найти плотность распределения СВНТ Решение. Ответ: Пример 3. Случайная величина X распределена нормально с параметрами m и Решение. Напишем плотность распределения случайной величины X: Применим формулу Отсюда видно, что
Пример 4. Случайная величина X распределена по закону Коши Найти плотность распределения случайной величины Решение. Таким образом, Ответ:
Пример 5. Случайная величина X распределена равномерно в интервале Решение. Найдем плотность распределения Из уравнения Найдем производные обратных функций: Тогда модули производных равны Учитывая, что Отсюда Так как Ответ: Рассмотрим далее на примерах, как находится функция распределения
Пример 2.3.6. Задана функция распределения Решение. 1) По определению функции распределения Из уравнения 2) По определению функции распределения Из уравнения Ответ: 1)
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 554; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

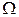 , F, P) задана случайная величина X. Предположим, что имеется числовая функция
, F, P) задана случайная величина X. Предположим, что имеется числовая функция  скалярного аргумента x. Случайную величину
скалярного аргумента x. Случайную величину  назовем функцией от одномерной случайной величины X. Покажем, как построить закон распределения функции
назовем функцией от одномерной случайной величины X. Покажем, как построить закон распределения функции  , зная закон распределения случайного аргумента X.
, зная закон распределения случайного аргумента X. с вероятностями
с вероятностями  , где
, где  – множество возможных значений СВДТ X. Тогда для нахождения функции распределения можно воспользоваться соотношением
– множество возможных значений СВДТ X. Тогда для нахождения функции распределения можно воспользоваться соотношением .
.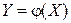 . Чтобы его построить, необходимо объединить в один столбец все одинаковые значения
. Чтобы его построить, необходимо объединить в один столбец все одинаковые значения  и
и  . Подставляя вместо аргумента x случайную величину Х, получим новые случайные величины
. Подставляя вместо аргумента x случайную величину Х, получим новые случайные величины  и
и  . Построить ряды распределений случайных величин: 1)
. Построить ряды распределений случайных величин: 1)  , 2)
, 2)  . Составить их функции распределения.
. Составить их функции распределения. ,
,  ,
,  ,
,  .
.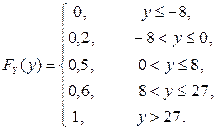
 :
: ,
,  ,
,  ,
,  .
. ,
,  ,
,  .
. и
и  , т.е.
, т.е. 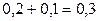 . Поэтому ряд распределения случайной величины Z имеет вид:
. Поэтому ряд распределения случайной величины Z имеет вид:
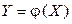 , где
, где  – гладкая строго монотонная функция скалярного аргумента x, а X – СВНТ с плотностью
– гладкая строго монотонная функция скалярного аргумента x, а X – СВНТ с плотностью 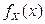 . Тогда плотность распределения
. Тогда плотность распределения  случайной величины Y находится по формуле:
случайной величины Y находится по формуле: ,
,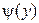 – обратная по отношению к
– обратная по отношению к  для каждого из интервалов монотонности, а затем представить
для каждого из интервалов монотонности, а затем представить  .
. и
и  , то
, то .
. (
(  ), где СВНТ X имеет плотность
), где СВНТ X имеет плотность  .
. при
при  . Отсюда
. Отсюда  . Таким образом,
. Таким образом, .
. (
(  ). Доказать, что линейная функция
). Доказать, что линейная функция 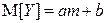 ,
,  .
. .
. .
. .
. .
. .
.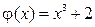 гладкая строго монотонная функция. Тогда обратная функция
гладкая строго монотонная функция. Тогда обратная функция  . Отсюда
. Отсюда  , причем
, причем  . Значит,
. Значит,  .
. .
. (
(  ). Найти плотность распределения случайной величины
). Найти плотность распределения случайной величины  .
. случайной величины X:
случайной величины X:
 найдем обратную функцию
найдем обратную функцию 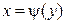 . Поскольку в интервале
. Поскольку в интервале  и
и  , в которых эта функция монотонна. На интервале
, в которых эта функция монотонна. На интервале  , на интервале
, на интервале  . Тогда искомая плотность распределения может быть найдена из равенства
. Тогда искомая плотность распределения может быть найдена из равенства ,
,  .
. ,
,  .
.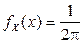 при
при  , получим
, получим ,
,  .
. .
. . Таким образом, на интервале
. Таким образом, на интервале  искомая плотность распределения равна
искомая плотность распределения равна 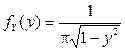 , вне этого интервала
, вне этого интервала  .
.
 случайной величины
случайной величины  случайной величины X.
случайной величины X. ; 2)
; 2) 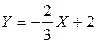 .
. . Поскольку функция
. Поскольку функция  – возрастающая, то неравенство
– возрастающая, то неравенство  выполняется, если имеет место неравенство
выполняется, если имеет место неравенство  , поэтому
, поэтому .
. . Тогда
. Тогда .
. – убывающая, то неравенство
– убывающая, то неравенство  , поэтому
, поэтому .
. . Тогда
. Тогда .
.


