
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства математического ожидания и дисперсииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если существуют соответствующие моменты, то справедливы следующие свойства математического ожидания и дисперсии: 1. 2. Для любых случайных величин X и Y: (аддитивное свойство математического ожидания). Замечание. Для любых случайных величин 3. Для любой константы c: 4. Для любых случайных величин X и Y: если В частности, если 5. Для любой случайной величины X: если 6. Для любой случайной величины X: 7. Для любой случайной величины X: (свойство неотрицательности дисперсии). 8. Для любой константы c: 9. Для любых случайных величин X и Y: В частности, если случайные величины X и Y некоррелированны, то (мультипликативное свойство математического ожидания). Замечание. Отметим, что для случайных величин недостаточно условия некоррелированности 10. Для любых случайных величин X и Y: Замечание. Для любых случайных величин В частности, если случайные величины X и Y некоррелированны, то (аддитивное свойство дисперсии). Замечание. Если случайные величины Отметим также, что поскольку из независимости случайных величин следует их некоррелированность, то свойство 10 выполняется и для независимых случайных величин. Пример 2.3.20. Известно, что случайная величина имеет биномиальное распределение Решение. По свойству 8 математического ожидания и дисперсии Вычислим теперь Поскольку для случайной величины Ответ:
Пример 2.3.21. Функция распределения СВНТ X имеет вид: Найти Решение. По условию задачи случайная величина X распределена по экспоненциальному закону: По свойству 8 математического ожидания и дисперсии: Ответ: Пример 2.3.22. Известно, что Решение. Используя формулу для дисперсии суммы получим Ответ:
Пример 2.3.23. На столе налогового инспектора лежат три декларации от представителей трех различных групп населения. Вероятности сокрытия доходов при заполнении декларации для одного представителя каждой группы равны соответственно 0,05, 0,1 и 0,15. Предположим, что сокрытие доходов обнаруживается при проверке в 100% случаев. Найти средний доход государства от проверки этих деклараций, если сумма налагаемого штрафа при обнаружении сокрытия дохода составляет по группам населения 100, 250 и 500 минимальных окладов соответственно. Решение. Рассмотрим случайную величину X, равную доходу государства от проверки трех деклараций. Тогда X можно представить в виде где Поскольку для индикаторных случайных величин Ответ: средний доход государства от проверки поданных трех деклараций составит 105 минимальных окладов.
Пример 2.3.24. Известно, что случайные величины X и Y (где X – рост наугад взятого взрослого мужчины и Y – его вес) удовлетворительно описываются нормальным законом распределения: Решение. Так как случайные величины X и Y распределены нормально, то разность Таким образом, Ответ:
Упражнения 2.3.13. СВНТ X имеет плотность вероятности Найти 2.3.14. Плотность вероятности случайной величины X имеет следующий вид: Найти 2.3.15. Пусть существуют дисперсии случайных величин X и Y такие, что 2.3.16. Известно, что случайная величина 2.3.17. Известно, что случайная величина 2.3.18. Известно, что случайные величины 2.3.19. Подбрасывают три игральные кости. Рассматриваются случайные величины: X – количество костей, на которых выпало шесть очков, Y – количество костей, на которых выпало пять очков. Найти 2.3.20. Предприятие имеет две поточные линии по сборке некоторой продукции. Технологические процессы на линиях связаны между собой. Рассматривая в качестве случайной величины X – количество единиц продукции, собранной за день на первой линии, а Y – на второй линии, совместное распределение этих величин можно задать с помощью таблицы:
Составить закон распределения случайной величины
Ответы к упражнениям 2.3.13. 2.3.14. 2.3.15. 0. 2.3.16. 0. 2.3.17. 0. 2.3.18. 2.3.19. 2.3.20.
Характеристическая функция Если Определение. Характеристической функцией случайной величины X называется комплекснозначная функция где В частности, Замечание 1. По характеристической функции Замечание 2. Характеристическая функция представляет собой преобразование Фурье плотности вероятности Таким образом, для СВНТ задание Характеристическая функция 1. 2. 3. Если существует m -й абсолютный момент 4. Если 5. Если Замечание. Пользуясь этим свойством, можно решать задачу определения закона распределения суммы независимых случайных величин (задачи композиции). Действительно, если 6. Определение. Характеристической функцией случайного вектора
Пример 2.3.25. Найти характеристическую функцию случайной величины X, имеющей биномиальное распределение ( Решение. Согласно определению характеристической функции СВДТ X По свойству 3 для Отсюда
Пример 2.3.26. Найти характеристическую функцию случайной величины X, имеющей пуассоновское распределение ( Решение. Согласно определению характеристической функции СВДТ X По свойству 3 для Отсюда
Пример 2.3.27. Найти характеристическую функцию случайной величины X, имеющей геометрическое распределение ( Решение. Согласно определению характеристической функции СВДТ X По свойству 3 для Отсюда
Пример 2.3.28. Найти характеристическую функцию случайной величины X, имеющей равномерное распределение ( Решение. Согласно определению характеристической функции СВНТ X Замечание. Для случайной величины
Пример 2.3.29. Найти характеристическую функцию случайной величины X, имеющей показательное распределение ( Решение. Согласно определению характеристической функции СВНТ X По свойству 3 для Отсюда
Пример 2.3.30. Найти характеристическую функцию случайной величины X, имеющей нормальное распределение ( Решение. Найдем вначале характеристическую функцию случайной величины Дифференцируя Решая это дифференциальное уравнение с разделяющимися переменными при начальном условии Рассмотрим теперь случайную величину Найдем теперь математическое ожидание, дисперсию и среднее квадратическое отклонение Отсюда Пример 2.3.31. Проверить композиционную устойчивость нормального закона. Решение. Пусть независимые случайные величины X и Y имеют нормальное распределение: Откуда видно, что характеристическая функция
Упражнения 2.3.21. Задана характеристическая функция СВНТ X: Найти плотность 2.3.22. Случайные величины X и Y независимы и распределены по закону Пуассона: 2.3.23. Случайные величины X и Y независимы и распределены по биномиальному закону: 2.3.24. Случайные величины X и Y независимы и распределены по одному закону
Ответы к упражнениям 2.3.21. 2.3.24. Нет. http://michael983.narod.ru/t/5.htmКонец формы
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

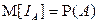 , где
, где  – индикатор события А.
– индикатор события А.
 из свойства 2 по индукции выводится:
из свойства 2 по индукции выводится: .
. ,
,  .
. , то
, то  .
. , то
, то  .
. , то
, то  .
. .
.
 ,
, 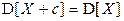 .
. (или
(или 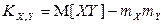 ).
).
 , для выполнения свойства
, для выполнения свойства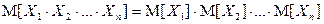
 .
. .
.
 некоррелированны, то
некоррелированны, то .
. . Найти
. Найти 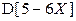 и
и  .
. . Поскольку для случайной величины
. Поскольку для случайной величины  дисперсия
дисперсия  , где по условию задачи
, где по условию задачи  ,
,  ,
,  , то
, то .
. .
. и, по свойству 6,
и, по свойству 6,  , то
, то .
. ,
,  .
.
 и
и  .
. . Поэтому
. Поэтому 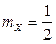 ,
,  . Найдем вначале
. Найдем вначале  :
:  . Тогда:
. Тогда:
 .
. .
. ,
,  .
. ,
,  ,
,  . Найти
. Найти  и
и  .
. . Тогда
. Тогда .
. ,
,  .
. ,
, (
(  ) индикаторные случайные величины, т.е.
) индикаторные случайные величины, т.е.  , если подавший декларацию представитель i -й группы населения скрывает доход, и
, если подавший декларацию представитель i -й группы населения скрывает доход, и  – в противном случае. По условию задачи требуется найти средний доход государства от проверки налоговых деклараций, т.е. математическое ожидание случайной величины X. Воспользуемся свойствами математического ожидания для вычисления
– в противном случае. По условию задачи требуется найти средний доход государства от проверки налоговых деклараций, т.е. математическое ожидание случайной величины X. Воспользуемся свойствами математического ожидания для вычисления  :
: .
.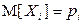 (
(  .
. ,
,  . Ковариация этих признаков равна
. Ковариация этих признаков равна  . Считается, что человек страдает избыточным весом, если выполняется неравенство
. Считается, что человек страдает избыточным весом, если выполняется неравенство  . Найти математическое ожидание и дисперсию характеристики избыточного веса
. Найти математическое ожидание и дисперсию характеристики избыточного веса  , а также вероятность того, что наугад выбранный мужчина страдает избыточным весом.
, а также вероятность того, что наугад выбранный мужчина страдает избыточным весом. ;
; 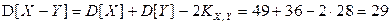 .
. и, следовательно,
и, следовательно, .
. ,
,  ,
,  .
. .
. и
и  .
.
 и
и  .
. . Чему равна ковариация случайных величин
. Чему равна ковариация случайных величин  и
и  ?
? ,
,  . Найти
. Найти  . Пусть
. Пусть  . Найти
. Найти 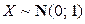 ,
,  . Вычислить
. Вычислить  .
. и закон распределения случайной величины
и закон распределения случайной величины  .
.
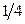

 и
и  .
. ,
,  .
. ,
,  .
. .
. ,
,  .
.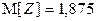 ,
,  ; закон распределения Z:
; закон распределения Z: – комплекснозначная случайная величина, где X и Y – действительные случайные величины, то
– комплекснозначная случайная величина, где X и Y – действительные случайные величины, то .
. ,
, ,
,  .
. , если X – СВДТ;
, если X – СВДТ; , если X – СВНТ.
, если X – СВНТ. однозначно восстанавливается функция распределения
однозначно восстанавливается функция распределения  .
.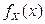 СВНТ X. Поэтому обратное преобразование Фурье приводит к соотношению
СВНТ X. Поэтому обратное преобразование Фурье приводит к соотношению .
.
 .
.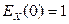 .
. , то существуют производные характеристической функции
, то существуют производные характеристической функции  , где
, где  .
. , то
, то  .
. , причем
, причем  независимы в совокупности, то
независимы в совокупности, то  .
. . Найдя
. Найдя  , можно по характеристической функции восстановить закон распределения случайной величины Z. Кроме того, по виду
, можно по характеристической функции восстановить закон распределения случайной величины Z. Кроме того, по виду  , где черта означает операцию комплексного сопряжения. В частности, отсюда следует, что если
, где черта означает операцию комплексного сопряжения. В частности, отсюда следует, что если  называется комплекснозначная функция n действительных переменных
называется комплекснозначная функция n действительных переменных  , определяемая равенством
, определяемая равенством .
. ), и с ее помощью вычислить
), и с ее помощью вычислить  ,
, 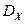 и
и  .
. .
.
 ,
,

 .
. ,
, 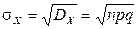 .
. ), и с ее помощью вычислить
), и с ее помощью вычислить  .
.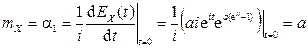 ,
,
 .
. ,
,  .
. ), и с ее помощью вычислить
), и с ее помощью вычислить  .
. ,
,
 .
.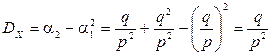 ,
,  .
. ).
). .
.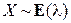 ), и с ее помощью вычислить
), и с ее помощью вычислить  .
. ,
, ,
, ,
,  .
. ), и с ее помощью вычислить
), и с ее помощью вычислить  . Согласно определению характеристической функции СВНТ X
. Согласно определению характеристической функции СВНТ X

 .
. (свойство 2 характеристической функции), находим
(свойство 2 характеристической функции), находим  . Отсюда характеристическая функция случайной величины
. Отсюда характеристическая функция случайной величины  .
. имеет нормальное распределение
имеет нормальное распределение 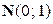 и, следовательно, характеристическую функцию
и, следовательно, характеристическую функцию  . Далее, по свойству 4 характеристической функции, для случайной величины
. Далее, по свойству 4 характеристической функции, для случайной величины  имеем
имеем .
. ,
, ,
, ,
,  .
. ,
,  . Найдем
. Найдем  .
. . Значит, нормальный закон является композиционно устойчивым.
. Значит, нормальный закон является композиционно устойчивым. .
. распределения случайной величины X.
распределения случайной величины X. ,
,  . С помощью характеристической функции доказать композиционную устойчивость закона Пуассона.
. С помощью характеристической функции доказать композиционную устойчивость закона Пуассона. ,
,  . С помощью характеристической функции доказать композиционную устойчивость биномиального закона.
. С помощью характеристической функции доказать композиционную устойчивость биномиального закона. . Является ли закон
. Является ли закон  – распределение Коши.
– распределение Коши.


