
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистической гипотезы о матожидании нормального распределения при известной дисперсииСодержание книги
Поиск на нашем сайте
Пусть имеется нормально распределенная СВ x. D x = s 2. Матожидание M x неизвестно. Допустим, что M x = a, где a – некоторое число. Будем считать также, что имеется другая информация, указывающая на то, что M x = a 1, где a 1 > a.
Выдвигаем нулевую гипотезу H 0: M x= a; при конкурирующей гипотезе H 1: M x= a 1 Делаем выборку объема n: x 1, x 2,..., xn . В основе проверки лежит тот факт, что СВ В качестве статистического критерия выбирается случайная величина z=(
По принятому уровню значимости (ошибка 1 рода) a (например a = 0,05), используя то, что случайная величина z имеет НЗР, определим значение K кр: a = P (K кр < z < ¥) = F(¥) – F(K кр) = 0,5 – F(K кр). Отсюда, Ф(Kкр)=(1–2a)/a и осталось воспользоваться таблицей функции Лапласа для нахождения числа K кр.
Если величина z, полученная при выборочном значении
Если в задаче поставить другое условие: H 0: M x = a; H 1: M x = a 1 , a 1 < a, то критическая область здесь левосторонняя.
Рассмотрим теперь такую задачу: H 0: M x= a; H 1: M x¹ a. В данном случае большие отклонения величины z от нуля в положительную или отрицательную сторону должны приводить к заключению о ложности гипотезы H 0, то есть здесь следует рассматривать двустороннюю критическую область. Критическое значение K кр определяется с помощью соотношения P (- K кр< z < K кр) =1– a =F(K кр)–F(– K кр)=2F(K кр). Из этого соотношения следует: F(K кр)= (1–a)/a.
Важнейшие распределения в математической статистике: распределение хи-квадрат, распределение Стьюдента. Распределение χ2 (хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимых стандартных нормальных СВ.
Пусть Uk, Свойства распределения хи-квадрат: 1) СВ Xn имеет следующую плотность распределения:
2) Характеристическая функция СВ Xn имеет вид 3) СВ Xn имеет следующие моменты: М(Xn)=n, D(Xn)=2n. 4) Сумма любого числа m независимых СВ Xk, 5) Распределение хи-квадрат обладает свойством асимптотической нормальности: Распределение Стьюдента Распределение Стьюдента – это однопараметрическое семейство абсолютно непрерывных распределений. Пусть U и Xn - независимые СВ, U~N(0;1), Xn~χ2(n). Тогда СВ Tn=U/(√Xn/n) имеет распределение Стьюдента с n степенями свободы, что обозначают как Tn~S(n). Свойства распределения Стьюдента: 1) СВ Tn имеет плотность распределения Графики плотностей f(t,n), называемые кривыми Стьюдента, симметричны при всех n=1,2,… относительно оси ординат:
2) СВ Tn имеет матожидание, равное M(Tn)=0 для всех n≥2, и дисперсию D(Tn)=n/(n-2) при n>2. При n=2 дисперсия D(Tn)=+∞. 3) При n→∞ распределение S(n) асимптотически нормально, т.е. Tn→U, где СВ U имеет распределение N(0;1). При n≥30 распределение С. S(n) практически не отличается от N(0;1).
Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин. Пусть X1….Хk совместно независимые стандартные нормальные случайные величины, то есть: Тогда случайная величина
Следовательно, плотность распределения хи-квадрат имеет вид
Плотность вероятности: Функция распределения
Распределение Стьюдента Распределение Стьюдента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Пусть Y0,Y1, ………Yn независимые стандартные нормальные случайные величины, такие что Тогда распределение случайной величины t, где
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.105.32 (0.009 с.) |

 (выборочная средняя) распределена по нормальному закону с дисперсией s2/ n и математическим ожиданием, равным a в случае справедливости H 0, и равным a 1 в случае справедливости H 1.
(выборочная средняя) распределена по нормальному закону с дисперсией s2/ n и математическим ожиданием, равным a в случае справедливости H 0, и равным a 1 в случае справедливости H 1.

 – набор из n независимых нормально распределенных СВ, Uk~N(0;1). Тогда СВ
– набор из n независимых нормально распределенных СВ, Uk~N(0;1). Тогда СВ  имеет распределение хи-квадрат (χ2-распределение) с n степенями свободы, что обозначается как Xn~χ2(n).
имеет распределение хи-квадрат (χ2-распределение) с n степенями свободы, что обозначается как Xn~χ2(n). , где
, где  – гамма-функция. Графики функций f(x,n), называемые кривыми Пирсона, ассиметричны и начиная с n>2 имеют один максимум в точке x=n-2:
– гамма-функция. Графики функций f(x,n), называемые кривыми Пирсона, ассиметричны и начиная с n>2 имеют один максимум в точке x=n-2:

 , имеющих распределение хи-квадрат с nk степенями свободы, имеет распределение хи-квадрат с
, имеющих распределение хи-квадрат с nk степенями свободы, имеет распределение хи-квадрат с  степенями свободы.
степенями свободы. , где СВ U имеет распределение N(0;1). Это означает, что при достаточно большом объеме n выборки можно приближенно считать Xn~N(n;2n). Фактически эта аппроксимация имеет место уже при n≥30.
, где СВ U имеет распределение N(0;1). Это означает, что при достаточно большом объеме n выборки можно приближенно считать Xn~N(n;2n). Фактически эта аппроксимация имеет место уже при n≥30.

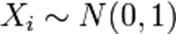
 имеет распределение хи-квадрат с k степенями свободы, обозначаемое
имеет распределение хи-квадрат с k степенями свободы, обозначаемое 
 Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:
Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:
 а его функция распределения
а его функция распределения


 называется распределением Стьюдента с n степенями свободы. Пишут
называется распределением Стьюдента с n степенями свободы. Пишут  Её распределение абсолютно непрерывно и имеет плотность
Её распределение абсолютно непрерывно и имеет плотность  где
где  — гамма-функция Эйлера.
— гамма-функция Эйлера.


