
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебра событий. Основные операции над событиями. Теорема сложения вероятностей. Следствия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие события в теории вероятностей, вероятность события, достоверное событие, невозможное событие. Классическая формула вычисление вероятности (схема «случаев»), частотная интерпретация вероятности (свойство устойчивости частот). Теория вероятностей – матем. наука, изучающая закономерности случайных явлений (С.Я.). С. Я. – явление, которое при неоднократном повторении одного и того же опыта протекает каждый раз по-иному. Событие – факт, который в результате опыта может произойти или не произойти. (А = {появление герба при подбрасывании монеты}, В = {появление трех гербов при 3кратном подбрасывании}. Вероятность события – числовая хар-ка степени возможности появления какого-либо случайного события при тех или иных условиях. Р(А). Достоверное событие – событие, вероятность которого равна 1; это то событие, которые обязательно произойдет. Р(Ω)=1 (выпадение не более 6 очков при подбрасывании играл. кубика). Недостоверное – вероятность меньше 1. Невозможное событие – вероятность равна 0. Р(Ø)=0. Классическая формула вычисление вероятности: P=mA/n, где n – общее число случаев, mA — число случаев, благоприятных событию А (обеспечивающих его появление). Здесь предполагается, что элементарные исходы не совместны, равновозможные и образуют полнeую группу: - события называются несовместными, если никакие 2 из них не могут появиться вместе (выстреле - попад/промах) - несколько событий наз-ся равновозможными, если по условию симметрии можно считать, что ни одной из этих событий не является объективно более возможным, чем другое (выпадение любого числа от 1 до 6 при подбрасывании кубика) - несколько события образуют полную группу, если в результате опыта должно появиться хотя бы одно из них (появление 1,2,3,4,5,6 очков при подбрасывании; хотя бы 1 промах и хотя бы 1 попадание при 2 выстрелах) Частота события в серии из N опытов – отношение числа опытов, в которых это событие произошло, к общему числу произведенных опытов. Р*(А)=m/n Частоту события иначе называют его статистической вероятностью. Именно статистика массовых случайных явлений — база для определения вероятностей событий в опытах, не обладающих симметрией возможных исходов. Случайные обстоятельства, сопровождающие каждый отдельный опыт, в массе опытов взаимно погашаются, и частота постепенно стабилизируется, приближаясь, с незначительными колебаниями, к некоторой средней, постоянной величине.
Условная вероятность. Теорема умножения вероятностей. Следствия. Независимость событий. Вероятность Р(В) как мера степени объективной возможности наступления события В имеет смысл при выполнении определенного комплекса условий. При изменении условий вероятность события В может измениться. Так, если к комплексу условий, при котором изучалась вероятность Р(В), добавить новое условие А, то полученная вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В и обозначается РА(В), или Р(В/А), или Р(В|А). Теорема умножения вероятностей – вероятность произведения двух событий равна произведению вероятности его события на условную вероятность второго события при условия, что первое событие произошло. Р(АВ) = Р(А) * Р(В|А). Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от А. Следствие 2. Вероятность произведения двух независимых событий равна Р(АВ) = Р(А) * Р(В). Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого. Например, кость брошена 2 раза. Вероятность появления 2 при втором бросании не зависит от появления 1 при первом. Несколько событий называются независимыми, если независимы любые два из них и независимы любое из данных событий и любые комбинации остальных событий. В противном случае события называются зависимыми. Напр., 3 события А, В и С независимы, если независимы события А и В, А и С, В и С, А и ВС, В и АС, С и АВ.
Биномиальное распределение. Частная теорема о повторении опытов. Примеры. БР – распределение количества успехов в последовательности независимых случайных экспериментов таких, что вероятность успеха в каждом из них равна Р. Дискретная СВ Х имеет биномальный закон распределения с параметрами n и p, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями P(Х=m)n=Сnmpmqn-m, где 0<p<1, q=1-p. Биномиальный закон распределения представляет собой закон распределения числа X=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p.
y~Bi(n,p) (y имеет биномиальное распределение, где n – количество испытаний, p – вер-ть успеха в каждом испытании) M(Y) = np; D(Y) = npq (M(m/n)=p; D(m/n)=pq/n) Ассиметрия – Sk =(q-p)/(√npq) Эксцесс – Еx =(1-6pй)/(npq)
Теорема. Если вероятность p наступления события А в каждом испытании постоянная, то вероятность Pm,n того, что событие А наступит m раз в n независимых опытах равна Сnmpmqn-m где q=1-p. (формула Бернулли). Примеры: 1) Вероятность изготовления на станке стандартной детали равна 0,8. Найти вер-ти возможного числа появления брак. деталей среди пяти отобранных. Р0,5= С500,200,85. Р1,5. Р2,5. Р3,5. Р4,5. Р5,5. 2) Вероятность того, что расход э/энергии в продолжение 1 суток не превысит уст. нормы, равна p=0,75. Найти вер-ть того, что в ближ. 6 суток расход э/энергии в теч. 4 суток не превысит нормы. Р6(4) = С64p4q2 = С62p4q2 = (6*5)/(1*2) * (0,75)4 * (0,25)2 = 0,3
Производящая ф-ю вероятности Рm,n. Zm –искомая вероятность.
Закон Пуассона моделирует СВ, представляющую собой число событий, произошедших за фикс. время при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Данное распр-е играет важную роль в теории масс. обслуж-я. Рассмотрим дискретную СВ Х, которая может принимать значения 0, 1, 2 и т.д. (целые неотрицательные). Pm = P(X=m) = 𝜆m/m! * e-𝜆 , где 𝜆 – параметр данного распределения. х~P(𝜆) M(X)=𝜆 D(X)=𝜆 Ассиметрия – Sk =𝜆-1/2 Эксцесс – Еx =𝜆-1 Поток событий – последовательность событий, которые наступают в случайные моменты времени. Простейший – поток событий, обладающий свойствами: - стационарности: вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета (вероятность попадения того или иного числа событий на участок времени, зависит только от длины этого участка). - отсутствия последействия: вероятность появления k на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка (вероятность не зависит от момента совершения предыдущих событий). - ординарности: вероятностью наступления за элементарный промежуток времени более одного события можно пренебречь по сравнению с вероятностью наступления за этот промежуток не более одного события (вероятность одновременного появления двух и более событий равна нулю). Интенсивность потока (λ) – среднее число событий, которые появляются в единицу времени. Формула Пуассона. Предположим, что мы хотим вычислить вероятность Pm,n появления события А при большом числе испытаний n, например P300,500. По формуле Бернулли: С300500p300q200 = 500!/(300!*200!) * p300q200. В этом случае непосредственное вычисление по формуле Бернулли технически сложно. Поэтому возникает естественное желание иметь более простые приближенные формулы для вычисления Pm,n при больших n. Наиболее простой из них является формула Пуассона. Теорема. Если вероятность p наступления события А в каждом испытании стремится к нулю (р→0) при неограниченном увеличении числа n испытаний (n→∞), причем произведение np стремится к постоянному числу 𝜆 (np→𝜆), то вероятность Pm,n того, что событие А появится m раз в n независимых испытаниях, удовлетворяет предельному равенству:
Вероятность появления хотя бы одного события:
Пример. Найти вероятность того, что за 2 минуты придет хотя бы один вызов. P(X≥1) = 1-P(X<1) = 1-P(X=0) =
Понятие о системе случайных величин. Геометрическая интерпретация. Дискретный двумерный вектор. Совместные и частные законы распределения случайного вектора. Функция распределения, свойства. Условные законы распределения. Зависимые и независимые СВ.
Наряду с одномерными СВ рассматриваются многомерные СВ. Очень часто результат испытания характеризуется не одной СВ, а некоторой системой СВ, которую также называют многомерной СВ или случайным вектором. Например, точность попадания снаряда – координаты х и у – пример двумерной СВ. Геометрическая интерпретация СВ: 1) Система двух СВ может изображаться такой на плоскости Оху, х – абсцисса, у – ордината 2) Систему двух СВ можно рассматривать как вектор на плоскости ху. Если ζ и η – дискретные СВ – вектор дискретный, если ζ и η – непрерывные, вектор непрерывный. Дискретный двумерный вектор – геом. изображение СВ на плоск-ти Оху, Х и Y – составляющие этого вектора.
Поскольку события {ζ=xi; η=yi} образуют полную группу, то получается: Чтобы по таблице распределения найти вероятность того, что одномерная СВ примет определенное значение, надо просуммировать вероятности pij из соответствующей этому значению строки (столбца) данной таблицы. Частным законом СВ ζ называется набор вероятностей событий {ζ=x}. Если задан совместный закон распределения, то частный получается следующим образом:
(суммируется строка) (суммируется столбец)
Функция распределения n-мерной СВ: F(x1, x2, …, xn) = P(X1<x1, X2<x2, …, Xn<xn) В двумерном случае для СВ (X,Y): F(x, y) = P(X< x, Y<y)
(суммирование вер-тей распространяется на все i, для кот. xi<x, и все j, для кот. yj<y).
Свойства функции распределения: 1. F(x,y) не убывающая функция обоих своих аргументов, т.е. при x1<x2: F(x1, y)≤F(x2, y) и при y1<y2: F(x, y1)≤F(x, y2). 2. Повсюду на -∞ функция равна 0: F(-∞,y)=0, F(x,-∞)=0 3. При одном из аргументов, равном +∞, функция распределения (совместный закон распределения) превращается в функцию распределения СВ, соответствующей другому аргументу (частный з. распред-я): F(+∞,y) = F2(y) F(х,+∞) = F1(x) 4. F(+∞,+∞)=1 5. 0≤F(x, y)≤1
Если зафиксировать значение одного из аргументов, например, положить Y=yj, то полученное распределение СВ Х называется условным распределением Х при условии Y=yj. Вероятности pj(хi) этого распределения будут условными вероятностями события Х=хi, найденными в предположении, что событие Y=yj произошло. Из определения условной вероятности:
Если величины независимы, то: F(x|y) = F1(x); f(x|y) = f1(x).
Аналогично условное распределение СВ Y при условии Х=хi задается с помощью условных вероятностей:
F(x,y) = F1(x)*F2(y) – совместный закон распределения
СВ Х и У называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла друга. В противном случае Х и У – зависимые. Для независимых СВ теорему умножения принимает вид: f(x,y)=f1(x)f2(y), т.е. плотность распределения системы независимых СВ равна произведению плотностей распределения отдельных величин, входящих в систему. СВ ζ и η называются независимыми, если для любых множеств a и b выполняется усл-е: P(ζ?A,η?B) = P(ζ?A)*P(η?B). Дискретные СВ ζ и η независимы тогда и только тогда, когда события ζ=xi и η=yj независимы для всех значений xi,yj.
Основные понятия математич. статистики. Простая статистическая совокупность. Статистическая функция распределения. Статистический ряд. Полигон. Гистограмма.
Разработка методов регистрации, описания и анализа математических экспериментальных данных получается в результат наблюдения массовых случайных явлений, составляющих предмет математической статистики (МС). Основные задачи МС: 1) Определение закона распределения СВ по стат.данным 2) Проверка правдоподобности гипотезы 3) Нахождения неизв-х параметров равномерного распределения Современную МС определяют как науку о принятии решений в условиях неопределенности. Главная задача МС состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Предположим, что СВ Х производит ряд опытов с целью определения либо закона ее распределения (заранее неизвестного), либо с целью проверки гипотезы о законе распределения. В каждом из опытов СВ Х принимает определенное значение – варианту. Причем последовательность x1,…xn значений СВ Х (где x1<…<xn) получена в результате ранжирования (операции расположения СВ по возрастанию).
Совокупность вариант представляет первичный стат. материал и называется простой стат. совокупностью или статистическим рядом. Обычно эти данные представлены в виде таблицы. На их основе строится функция распределения. Стат. функция распределения представляет собой ступенчатую функцию. Величина скачка данной функции – частота события при неограниченном числе опытов. Частота событий будет стремиться к подлинной.
Стат. ф-я распределения – функция F*(x), определяющая для каждого значения х относительную частоту события Х<x. F*(x)=nx/n, где nx - число вариант, меньших х, n – объем выборки.
Свойства стат. ф-и распределения: 1) значения функции принадлежат отрезку [0;1] 2) F*(x) – неубывающая функция 3) если х1 – наименьшая варианта, то F*(x)=0 при x≤x1; если хk – наибольшая варианта, то F*(x)1 при x>xk. Пример. Построить функцию F*n(x), если
Выборочная совокупность (выборка) – совокупность случайно отобранных объектов. Генеральная совокупность – совокупность объектов, из которых производится выборка. Объем совокупности – число объектов это совокупности.
Числа ni, показывающие сколько раз встречаются варианты xi в ряде наблюдений, называются частотами, а отношение их к объему выборке – частостями, т.е. p*i=ni/n. Для наглядности стат.распределение изображается графически в виде полигона и гистограммы. Полигон, как правило, служит для изображения дискретного (т.е. варианты отличаются на постоянную величину) стат. ряда.
Полигон является стат. аналогом многоугольника распределения (см. вопрос 7).
Для непрерывного распределения признака (т.е. варианты могут отличаться на сколь угодно малую величину) можно построить полигон частот, взяв середины интервалов в качестве значений
Площадь гистограммы частот = объему выборки, частностей = 1. Гистограмма частостей:
Гистограмма частот является стат.аналогом дифференциала функции распределения (плотности) f(x) СВ Х. Сумма площадей прямоугольников равна 1: h*p1*/h + … + pi*/h = pi* + … + pi* = 1, что соответствует условию Если соединить середины верхних оснований прямоугольников с отрезками прямой, то получим полигон того же распределения.
Точечные оценки параметров распределения. Требования, предъявляемые к точечным оценкам. Оценки для М(Х), D(X) и СДО. Большинство практических задач, которые решает статистика, состоит в оценивании некоторого количественного признака генеральной совокупности (совокупности объектов, явлений или процессов, из которых производится выборка). Предположим, что исследователю удалось установить, какому именно закону распределения подчиняется изучаемый количественный признак. В этом случае необходимо оценить параметры, которыми определяется предполагаемое распределение. Например, если удалось установить, что количественный признак подчиняется показательному закону распределения вероятностей, тогда необходимо оценить параметр λ, которым определяется данное распределение. Предположим, что имеются данные выборки, например, значения количественного признака x1, x2, …, xn, полученные в результате n наблюдений. Будем рассматривать x1, x2, …, xn как независимые СВ Х 1, Х 2, …, Х n. Статистическая оценка неизвестного параметра теоретического распределения – это функция от наблюдаемых случайных величин. Таким образом, определить статистическую оценку неизвестного параметра теоретического распределения, значит, определить функцию от наблюдаемых СВ Х 1, Х 2, …, Х n, которая дает приближ. значение оцениваемого параметра. Для того чтобы статистические оценки θi можно было бы принять за оценки параметров θi, необходимо и достаточно, чтобы оценки θi удовлетворяли трем статистическим свойствам: несмещенности, состоятельности и эффективности. θi называется несмещенной оценкой для параметра θi, если ее выборочное матожидание равно оцениваемому параметру генеральной совокупности. М(θi) = θi, М(θi) – θi = φi, где φi, - это смещение оценки. Смещенная оценка – это оценка параметра, чье матожидание не равно оцениваемому параметру, т.е. М(θi)≠θi, φi≠0.
θi является состоятельной оценкой для параметра θi, если она удовлетворяет закону больших чисел. Закон больших чисел гласит о том, что с увеличением выборки значение оценки θi стремится к значению параметра θi генеральной совокупности: Р(| θi – θi |<ε) → 1 при n → ∞. Для определения состоятельности оценки достаточно выполнения двух условий: 1) φi=0 или φi→0 при n→∞ - смещение оценки равно нулю или стремится к нему при объеме выборки, стремящейся к бесконечности. 2) D(θi) →0 при n→∞ - дисперсия оценки параметра θi стремится к нулю при объеме выборки, стремящемся к бесконечности. θi является эффективной оценкой для параметра θi, если статистическая оценка θi имеет наименьшую возможную дисперсию при заданном объеме выборки n.
Точечные оценки параметров распределения: Рассмотрим выборку x=(x1, x2, …, xn) значений генеральной совокупности Х. Пусть М(Х)=а, D(X)=σ2 генеральная средняя и дисперсия совокупности.
В качестве оценки для М(Х) используется выборочная средняя (средняя арифметическая выборки):
Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику – выборочную дисперсию. В качестве оценки для D(Х) используется выборочная дисперсия: Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой – средним квадратическим отклонением.
Выборочным средним квадратическим отклонением называют кв.корень из выборочной дисперсии: σ x =√σ x 2. x является несмещенной, состоятельной и эффективной оценкой для М(Х), причем σ Х 2=σ2/n. M(S2)=(n-1)/n*D(X), т.е. оценка S2 является смещенной. Чтобы избавиться от этого недостатка, для оценки неизвестной дисперсии генеральной совокупности пользуются исправленной несмещенной оценкой: При больших n (n>30) неизвестные параметры в формулах для дисперсии можно заменить на их выборочные без особой погрешности.
Метод моментов для нахождения точечных оценок неизв. параметров заданного распределения состоит в приравнивании теоретических моментов распределения соответствующим эмпирическим моментам, найденным по выборке. Так, если распределение зависит от одного параметра (например, задан вид плотности распределения f(х,0)), то для нахождения его оценки надо решить относительно θ одно ур-е: М(Х)= θ В (
Метод моментов является наиболее простым методов оценки параметров. Оценки метода моментов обычно состоятельны, однако их эффективность часто значительно меньше единицы. Пример. Найти оценки параметров СВ X~N(a,σ2). Требуется по выборке x1,…,xn найти точечные оценки неизвестных параметров a=M(X)=θ1 и σ2=D(X)=θ2. По методу моментов приравниваем их соответственно к выборочному среднему и выборочной дисперсии (α1=М(Х) – нач. момент 1 порядка, µ2=D(X) – центр. момент 2 порядка). Получаем
Статистические гипотезы. Основные понятия (основная и альтернативная гипотеза, критическая область, доверительная вероятность). Проверка статистических гипотез. Статистическая гипотеза представляет собой некоторое предположение о законе распределения СВ или о параметрах этого распределения, формулируемое на основе выборки.
Различают простую и сложную гипотезу. Простая, в отличие от сложной, однозначно определяет распред-е Р, т.е. Н: {P=P0}, а сложная – утверждает принадлежность распределения Р к некоторому семейству распределений – Н: {P?P0}. Примеры: П – {PA появления события в схеме Бернулли равна ½} С – {PA появления события в с.Бернулли заключена м/д 0,3 и 0,6} Г, в основе которых нет никаких допущений о конкретном виде закона распределения, называются непараметрическими, в противном случае – параметрическими. Нулевая (основная) Г – проверяемая Г. – Н0 – утверждает, что различия между сравниваемыми хар-ками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями. Альтернативная (конкур) – Н1 – противоречит Н0.
Проверка гипотезы основывается на вычислении некоторой СВ – критерия, точное или приближенное значение которого известно. Обозначение значения критерия: Z – функция от выборки: Z=(x1,…,xn). Процедура проверки гипотезы предполагает каждому значению критерия одно из двух решений – принять или отвергнуть Г. Тем самым, все выборочное пространство разделяется на 2 непересекающихся множества S0 и S1. Если значения критерия Z попадают в область S0, Г принимается, в S1 – отвергается, т.е.: S0 – область принятия Г (ОДЗ); S1 – область отклонения гипотезы (критическая). Принятие и отклонение гипотезы соответствует истине с некоторой вероятностью, возможны 2 рода ошибок:
Доверительная – вероятность того, что значение параметра генеральной совокупности находится в построенном для него доверительном интервале. Доверительная вероятность обычно обозначается (1-α) и выбирается из значений 0,9; 0,95; 0,99 и т.п. Оперативная хар-ка критерия – РА 1-α не допустить ошибку I рода, т.е. принять гипотезу Н0, когда она верна. Уровень значимости – РА α допустить ошибку I рода, т.е. отвергнуть гипотезу Н0, когда она верна. РА β допустить ошибку II рода, т.е. принять гипотезу Н0, когда она неверна. Мощность критерия – РА (1-β) не допустить ошибку II рода т.е. отвергнуть гипотезу Н0, когда она неверна.
Т.к. критерий Z – одномерная СВ, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы.
Области – критическая область: a) Правосторонняя – (kкр;+∞) b) левосторонняя – (-∞;kкр) c) двусторонняя (-∞;kкр)U(kкр;+∞)
# Пусть дана независимая выборка (X1,…,Xn)~N(µ,1), где μ – неизвестный параметр. Тогда Н0: {µ=µ0}, где μ0 – фиксированная константа, является простой гипотезой, а конкурирующая с ней Н1: {µ>µ0} – сложной.
27. Проверка статистических гипотез. Гипотеза о неизвестном среднем при известной дисперсии на примере нормального распределения. Проверка статистических гипотез – см. вопрос 26. Распределение Стьюдента Распределение Стьюдента – это однопараметрическое семейство абсолютно непрерывных распределений. Пусть U и Xn - независимые СВ, U~N(0;1), Xn~χ2(n). Тогда СВ Tn=U/(√Xn/n) имеет распределение Стьюдента с n степенями свободы, что обозначают как Tn~S(n). Свойства распределения Стьюдента: 1) СВ Tn имеет плотность распределения Графики плотностей f(t,n), называемые кривыми Стьюдента, симметричны при всех n=1,2,… относительно оси ординат:
2) СВ Tn имеет матожидание, равное M(Tn)=0 для всех n≥2, и дисперсию D(Tn)=n/(n-2) при n>2. При n=2 дисперсия D(Tn)=+∞. 3) При n→∞ распределение S(n) асимптотически нормально, т.е. Tn→U, где СВ U имеет распределение N(0;1). При n≥30 распределение С. S(n) практически не отличается от N(0;1).
Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин. Пусть X1….Хk совместно независимые стандартные нормальные случайные величины, то есть: Тогда случайная величина
Следовательно, плотность распределения хи-квадрат имеет вид
Плотность вероятности: Функция распределения
Распределение Стьюдента Распределение Стьюдента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Пусть Y0,Y1, ………Yn независимые стандартные нормальные случайные величины, такие что Тогда распределение случайной величины t, где
Понятие события в теории вероятностей, вероятность события, достоверное событие, невозможное событие. Классическая формула вычисление вероятности (схема «случаев»), частотная интерпретация вероятности (свойство устойчивости частот). Теория вероятностей – матем. наука, изучающая закономерности случайных явлений (С.Я.). С. Я. – явление, которое при неоднократном повторении одного и того же опыта протекает каждый раз по-иному. Событие – факт, который в результате опыта может произойти или не произойти. (А = {появление герба при подбрасывании монеты}, В = {появление трех гербов при 3кратном подбрасывании}. Вероятность события – числовая хар-ка степени возможности появления какого-либо случайного события при тех или иных условиях. Р(А). Достоверное событие – событие, вероятность которого равна 1; это то событие, которые обязательно произойдет. Р(Ω)=1 (выпадение не более 6 очков при подбрасывании играл. кубика). Недостоверное – вероятность меньше 1. Невозможное событие – вероятность равна 0. Р(Ø)=0. Классическая формула вычисление вероятности: P=mA/n, где n – общее число случаев, mA — число случаев, благоприятных событию А (обеспечивающих его появление). Здесь предполагается, что элементарные исходы не совместны, равновозможные и образуют полнeую группу: - события называются несовместными, если никакие 2 из них не могут появиться вместе (выстреле - попад/промах) - несколько событий наз-ся равновозможными, если по условию симметрии можно считать, что ни одной из этих событий не является объективно более возможным, чем другое (выпадение любого числа от 1 до 6 при подбрасывании кубика) - несколько события образуют полную группу, если в результате опыта должно появиться хотя бы одно из
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.012 с.) |

 Свойство устойчивости частот при большом числе однородных опытов – одна из наиболее характерных закономерностей, наблюдаемых в массовых С.Я. Если мы повторяем (воспроизводим) один и тот же опыт много раз (причем обеспечена независимость исходов отдельных опытов), частота события становится все менее случайной, выравнивается, приближается к постоянной.
Свойство устойчивости частот при большом числе однородных опытов – одна из наиболее характерных закономерностей, наблюдаемых в массовых С.Я. Если мы повторяем (воспроизводим) один и тот же опыт много раз (причем обеспечена независимость исходов отдельных опытов), частота события становится все менее случайной, выравнивается, приближается к постоянной.



 Соотношение между возможными значениями случайного вектора и их вероятностям называется совместным законом распределения. Совместный закон распред-я дискретных СВ задается набором вероятностей pij одновременного осуществления событий pij=p(ζ=xi; η=yi) и представляется в виде таблицы:
Соотношение между возможными значениями случайного вектора и их вероятностям называется совместным законом распределения. Совместный закон распред-я дискретных СВ задается набором вероятностей pij одновременного осуществления событий pij=p(ζ=xi; η=yi) и представляется в виде таблицы:

 Геометрически функция распределения F(x,y) означает вероятность попадания случайной точки (X,Y) в заштрихованную область – бесконечный квадрат, лежащий левее и ниже точки М(x,y). Правая и верхняя границы области не включаются – это означает, что функция распределения непрерывна слева по каждому из аргументов.
Геометрически функция распределения F(x,y) означает вероятность попадания случайной точки (X,Y) в заштрихованную область – бесконечный квадрат, лежащий левее и ниже точки М(x,y). Правая и верхняя границы области не включаются – это означает, что функция распределения непрерывна слева по каждому из аргументов. В случае дискретной СВ ее функция распределения определяется по формуле:
В случае дискретной СВ ее функция распределения определяется по формуле:




 Полигон частот – ломаная, отрезки которой соединяют точки с координатами (x1,n1),…,(xk,nk); полигон частостей (на рис.) – с координатами (x1,p1*),…,(xk,pk*). Варианты откладываются на оси абсцисс, а частоты и частости – на оси ординат.
Полигон частот – ломаная, отрезки которой соединяют точки с координатами (x1,n1),…,(xk,nk); полигон частостей (на рис.) – с координатами (x1,p1*),…,(xk,pk*). Варианты откладываются на оси абсцисс, а частоты и частости – на оси ординат.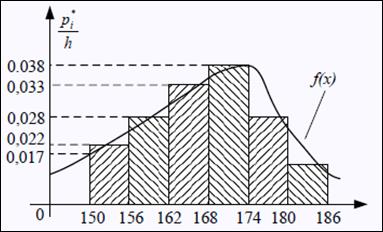 x1,…,xk. Гистограммая частот (частостей) – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/n. Плотность частоты – ni/h, частости – pi*/h.
x1,…,xk. Гистограммая частот (частостей) – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/n. Плотность частоты – ni/h, частости – pi*/h. для плотностей вероятностей f(x) (см. вопрос 11)
для плотностей вероятностей f(x) (см. вопрос 11)
 . Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.
. Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней. . Вычисление дисперсии можно упростить, используя формулу: S2= x2 - (x)2.
. Вычисление дисперсии можно упростить, используя формулу: S2= x2 - (x)2.

 есть функция от θ).
есть функция от θ). Если распределение зависит от двух параметров (например, вид плотности распределения f(x,θ1,θ2)) – надо решить относительно θ1 и θ2 систему уравнений:
Если распределение зависит от двух параметров (например, вид плотности распределения f(x,θ1,θ2)) – надо решить относительно θ1 и θ2 систему уравнений:  И, наконец, если надо оценить n параметров θ1, θ2, …, θn, - надо решить одну из систем вида:
И, наконец, если надо оценить n параметров θ1, θ2, …, θn, - надо решить одну из систем вида:
 Таким образом, искомые оценки параметров: θ1 =хВ и θ2 =√DВ.
Таким образом, искомые оценки параметров: θ1 =хВ и θ2 =√DВ. Они называются критическими.
Они называются критическими.

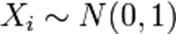
 имеет распределение хи-квадрат с k степенями свободы, обозначаемое
имеет распределение хи-квадрат с k степенями свободы, обозначаемое 
 Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:
Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:
 а его функция распределения
а его функция распределения


 называется распределением Стьюдента с n степенями свободы. Пишут
называется распределением Стьюдента с n степенями свободы. Пишут  Её распределение абсолютно непрерывно и имеет плотность
Её распределение абсолютно непрерывно и имеет плотность  где
где  — гамма-функция Эйлера.
— гамма-функция Эйлера.


