
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальные оценки. Доверительные интервалы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Большинство практических задач, которые решает статистика, состоит в оценивании некоторого количественного признака генеральной совокупности (совокупности объектов, явлений или процессов, из которых производится выборка). Предположим, что исследователю удалось установить, какому именно закону распределения подчиняется изучаемый количественный признак. В этом случае необходимо оценить параметры, которыми определяется предполагаемое распределение. Например, если удалось установить, что количественный признак подчиняется показательному закону распределения вероятностей, тогда необходимо оценить параметр λ, которым определяется данное распределение. Статистическая оценка неизвестного параметра теоретического распределения – это функция от наблюдаемых случайных величин. Существует оценка неизвестного параметра а одним числом. Такая оценка называется «точечной». Но в ряде задач требуется не только найти для параметра а подходящее значение, но и оценить его точность и надежность. Требуется знать – к каким ошибкам может привести замена параметра а его точечной оценкой Пусть для параметра а получена несмещенная оценка В этом случае β – доверительная вероятность, а интервал Iβ – доверительный интервал. Границы интервала Iβ: а1=
Данные понятия мы использовали в одном из пунктов домашней контрольной работы. Нам было необходимо построить доверительные интервалы для матожидания с надежностью β=0,95 и β=0,99.
где xi – среднее значение границ интервала, pi – вероятность попадания величины в интервал, n – количество результатов (объем выборки).
Статистические гипотезы. Основные понятия (основная и альтернативная гипотеза, критическая область, доверительная вероятность). Проверка статистических гипотез. Статистическая гипотеза представляет собой некоторое предположение о законе распределения СВ или о параметрах этого распределения, формулируемое на основе выборки.
Различают простую и сложную гипотезу. Простая, в отличие от сложной, однозначно определяет распред-е Р, т.е. Н: {P=P0}, а сложная – утверждает принадлежность распределения Р к некоторому семейству распределений – Н: {P?P0}. Примеры: П – {PA появления события в схеме Бернулли равна ½} С – {PA появления события в с.Бернулли заключена м/д 0,3 и 0,6} Г, в основе которых нет никаких допущений о конкретном виде закона распределения, называются непараметрическими, в противном случае – параметрическими. Нулевая (основная) Г – проверяемая Г. – Н0 – утверждает, что различия между сравниваемыми хар-ками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями. Альтернативная (конкур) – Н1 – противоречит Н0.
Проверка гипотезы основывается на вычислении некоторой СВ – критерия, точное или приближенное значение которого известно. Обозначение значения критерия: Z – функция от выборки: Z=(x1,…,xn). Процедура проверки гипотезы предполагает каждому значению критерия одно из двух решений – принять или отвергнуть Г. Тем самым, все выборочное пространство разделяется на 2 непересекающихся множества S0 и S1. Если значения критерия Z попадают в область S0, Г принимается, в S1 – отвергается, т.е.: S0 – область принятия Г (ОДЗ); S1 – область отклонения гипотезы (критическая). Принятие и отклонение гипотезы соответствует истине с некоторой вероятностью, возможны 2 рода ошибок:
Доверительная – вероятность того, что значение параметра генеральной совокупности находится в построенном для него доверительном интервале. Доверительная вероятность обычно обозначается (1-α) и выбирается из значений 0,9; 0,95; 0,99 и т.п. Оперативная хар-ка критерия – РА 1-α не допустить ошибку I рода, т.е. принять гипотезу Н0, когда она верна. Уровень значимости – РА α допустить ошибку I рода, т.е. отвергнуть гипотезу Н0, когда она верна. РА β допустить ошибку II рода, т.е. принять гипотезу Н0, когда она неверна. Мощность критерия – РА (1-β) не допустить ошибку II рода т.е. отвергнуть гипотезу Н0, когда она неверна.
Т.к. критерий Z – одномерная СВ, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы.
Области – критическая область: a) Правосторонняя – (kкр;+∞) b) левосторонняя – (-∞;kкр) c) двусторонняя (-∞;kкр)U(kкр;+∞)
# Пусть дана независимая выборка (X1,…,Xn)~N(µ,1), где μ – неизвестный параметр. Тогда Н0: {µ=µ0}, где μ0 – фиксированная константа, является простой гипотезой, а конкурирующая с ней Н1: {µ>µ0} – сложной.
27. Проверка статистических гипотез. Гипотеза о неизвестном среднем при известной дисперсии на примере нормального распределения. Проверка статистических гипотез – см. вопрос 26.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.011 с.) |

 и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы. Для этого пользуются доверительными интервалами и доверительными вероятностями.
и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы. Для этого пользуются доверительными интервалами и доверительными вероятностями.
 Но перед этим мы вычислили оценки матожидания и СДО, воспользовавшись формулами
Но перед этим мы вычислили оценки матожидания и СДО, воспользовавшись формулами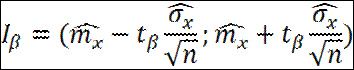 Для построения доверительных интервалов мы воспользовались формулой:
Для построения доверительных интервалов мы воспользовались формулой: Где tβ=argФ*[(1+β)/2] – табличное значение, равное для заданных значений доверительной вероятности. Данная величина определяет для нормального закона число СДО, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в данный участок была равна β.
Где tβ=argФ*[(1+β)/2] – табличное значение, равное для заданных значений доверительной вероятности. Данная величина определяет для нормального закона число СДО, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в данный участок была равна β. Они называются критическими.
Они называются критическими.



