
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывная случайная величина. Функция распределения и плотность вероятности. Их свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте СВ – величина, которая в результате опыта может принять то или иное значение, неизвестное заранее какое именно. Обозначается X = f (ω), где ω – элементарный исход. СВ обозначаются прописными буквами латинского алфавита X, Y, Z, а их значения – соотв-щим строчным буквам x, y, z. Законом распределения СВ называется любое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Непрерывная СВ – величина, бесконечное несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси (расход э/энергии за месяц, абсцисса точки попадания при выстреле). СВ Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, может быть, отдельных точек.
Непрерывная СВ имеет непрерывную ф-ю распределения. Она задает закон распределения, который полностью характеризует СВ. Функцией распределения СВ X называется функция F(x), выражающая для каждого х вероятность того, что СВ X примет значение, меньшее х: F(x)= Р(Х<х).
Свойства функции распределения: 1) F(x) – неубывающая функция своего аргумента: х1<х2, P(х1)<P(х2) 2) F(-∞)=1, F(+∞)=1 Теорема. Вероятность любо отдельно взятого значения непрерывной СВ равна нулю.
Следствие. Если Х – непрерывная СВ, то вероятность попадания СВ в интервал (х1;х2) не зависит от того, является ли этот интервал открытым или закрытым, т.е.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о СВ дает плотность вероятности СВ f(х) – производная ее функции распределения. f(х)=F’(x)
X~F(x) P(x<X<x+∆x) = F(x+∆x) – F(x)
ПР хар-т плотность, с которой распределяются значения СВ в заданной точке. Кривая, изображающая ПР – кривая распределения. ПР – одна из форм закона распределения СВ. Свойства ПР: 1. f(x)≥0; 2.
12. Числовые характеристики непрерывной СВ. М(Х), D(X), σx, их свойства. Иногда нет необходимости СВ характеризовать полностью, т.е. задавать ее закон распределения. Достаточно указать отд-е ее числ-е параметры, хар-щие существенные черты распределения. Среди числовых характеристик СВ можно выделить те, которые характеризуют положение СВ на числовой прямой, т.е. указывают некоторое среднее значение, около которого группируются все возможные значения СВ:
Если возможные значения принадлежат всей оси Х, то: f(х) – плотность вероятности СВ – производная ее функции распределения. f(х)=F’(x). ПР хар-т плотность, с которой распределяются значения СВ в заданной точке. Свойства матожидания: 1) M(C)=C 2) M(kX)=kM(X) 3) M(X±Y)=M(X)±M(Y) 4) M(XY) = M(X)M(Y) 5) M(X±C)=M(X)±C 6) M[X-M(X)]=0
принадлежат отрезку [a,b], то
Для вычисления D(X) можно использовать более удобные ф-лы:
Свойства дисперсии: 1) D(C)=C 2) D(kX)=k2D(X)
3) D(X) = M(X2) – [M(X)]2 4) D(X±Y)=D(X)±D(Y) 3. СДО:
4. Модой непрерывной СВ называется значение СВ, при котором плотность вероятности максимальна.
5. Медианой непрерывной СВ Х называется такое ее значение Ме, что Р(X<Me) = P (X>Ме). Для симметрич. распределения Мо, Ме и М(Х) совпадают.
7. Эксцесс Еx= µ4/σ4. 1 - Ek>0, 2 - Ek=0, 3 - Ek<0
8. Моменты непрерывной СВ Начальным моментом порядка k СВ Х называется матожидание величины Х k.
Начальный момент 1го порядка равен матожиданию. Центральным моментом порядка k случайной величины Х называется математическое ожидание величины (Х-mk)k.
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
В некоторых задачах встречаются величины, о которых заранее известно, что из возможных значения лежат в пределах некоторого определенного интервала, причем в пределах этого интервала все значения СВ равновероятны.
(b-a)c=1 → c=1/(b-a) (кривая распределения)
М(Х) = (a+b)/2 Мода Мо – любое число из [a;b] D(X) = (b-a)2/12 Медиана Ме = (a+b)/2 Ассиметрия Sk = 0 Эксцесс Ex = -1,2 µ4 =(b-a)4/80.
Равномерность попадания в интервал: P(α<x<β) = (β-α)(b-a)
Данный закон используется при анализе ошибок округления при проведении числовых расчетов (ошибка округления числа до целого распределена равномерно на отрезке [-0.5;0.5], в ряде задач масс. обслуж-я, при статистич. моделир-и наблюдений.
НЗР наиболее часто встречается на практике. Главная особенность состоит в том, что он является предельным законом, к которому приближаются другие законы распределения.
Непрерывная СВ Х имеет НЗР (закон Гаусса) с параметрам a и σ2, если ее плотность вероятности:
(горбик лев 1 и прав 2 – m2>m1, σ1=σ2) (горбик выше 1 и ниже 2 - m2=m1, σ1>σ2)
НЗР СВ с параметрами a=0 и σ2=1, т.е. N(0;1) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной (норм). Сложность непосредственного нахождения функции распределения СВ, имеющей НЗР, по формуле
Свойства функции Лапласа: 1. Ф(х) – четная, т.е. Ф(-х)=Ф(х) 2. Ф(х) – монотонно возрастающая, причем при х→+∞ Ф(х)→1 (практически можно считать, что уже при x>4 Ф(х)~4)
Теорема. Функция распределения СВ Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:
Свойства СВ, имеющую НЗР: 1. Вероятность попадания СВ Х в интервал [x1;x2] равна
2. Вероятность того, что отклонение СВ Х от матожидания не превысит величину ∆>0 равна P(|X-a|≤∆)=Ф(t), где t=∆/σ. Числовые характеристики: M(X) =a D(X) = σ2 µS=(S-1)*σ2*µS-2; µ2S+1=0 (нечетные);
Ассиметрия: А1=µ3/σ3=0 Эксцесс А2=µ4/σ4-3=0 –крутости по сравнению с нормальным.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 969; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |







 1. Матожиданием непрерывной СВ X, возможные значения которой принадлежат отрезку [a,b], называют определенный интервал:
1. Матожиданием непрерывной СВ X, возможные значения которой принадлежат отрезку [a,b], называют определенный интервал: 2. Дисперсией непрерывной СВ называется математической ожидание квадрата ее отклонения. Дисперсия - хар-ка рассеивания (разбросанности) значения СВ около ее матожидания. Если возможные значения Х
2. Дисперсией непрерывной СВ называется математической ожидание квадрата ее отклонения. Дисперсия - хар-ка рассеивания (разбросанности) значения СВ около ее матожидания. Если возможные значения Х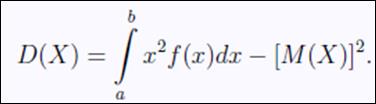




 6. Ассиметрия распределения – характеризует симметрию распределения относительно своего матожидания. Sk=µ3/σ3. Для симметрии распределения все моменты нечетного порядка равны нулю. 1 - Sk>0, 2 - Sk=0, 3 - Sk<0
6. Ассиметрия распределения – характеризует симметрию распределения относительно своего матожидания. Sk=µ3/σ3. Для симметрии распределения все моменты нечетного порядка равны нулю. 1 - Sk>0, 2 - Sk=0, 3 - Sk<0
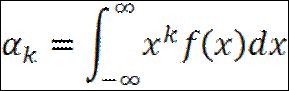

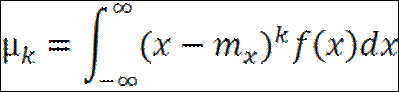

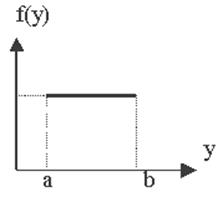 Х~R(a,b) – СВ Х имеет равномерный закон распределения на отрезке [a,b] и все значения она принимает с одинак. вер-тью:
Х~R(a,b) – СВ Х имеет равномерный закон распределения на отрезке [a,b] и все значения она принимает с одинак. вер-тью:
 Ф-я распределения СВ Х:
Ф-я распределения СВ Х: F(x) = P(X<x) =
F(x) = P(X<x) =
 F(x) =
F(x) =

 Сумма большого числа независимых СВ, подчиненных каким угодно законам распределения, приближенно подчиняется нормальному закону и это будет тем точнее, чем больше величин суммируется. X~N(a,σ2)
Сумма большого числа независимых СВ, подчиненных каким угодно законам распределения, приближенно подчиняется нормальному закону и это будет тем точнее, чем больше величин суммируется. X~N(a,σ2)
 и вероятности ее попадания на некоторый промежуток по формуле
и вероятности ее попадания на некоторый промежуток по формуле  связана с тем, что интеграл от функции Гаусса является «неберущимся» в элементарных функциях. Поэтому их выражают через функцию
связана с тем, что интеграл от функции Гаусса является «неберущимся» в элементарных функциях. Поэтому их выражают через функцию 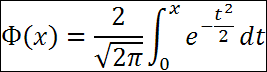 - функцию Лапласа, для которой составлены таблицы.
- функцию Лапласа, для которой составлены таблицы.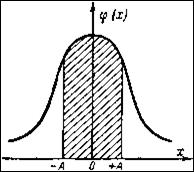 Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-x;x]:
Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-x;x]:
 , где
, где ;
;  .Вывод данной формулы:
.Вывод данной формулы: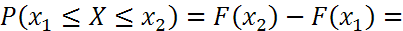


 , µ2=σ2=D(X); µ4=3σ4; µ6=15σ6.
, µ2=σ2=D(X); µ4=3σ4; µ6=15σ6.  «Правило трех сигм»: если СВ Х имеет нормальный закон распределения с параметрами а и σ2, т.е. N(a;σ2), то практически достоверно, что ее значения заключены в интервале (a-3σ; a+3σ). Нарушение данного правила, т.е. отклонение нормально распределенной СВ Х больше, чем на 3σ, является событием практически невозможным, т.к. его вероятность весьма мала:
«Правило трех сигм»: если СВ Х имеет нормальный закон распределения с параметрами а и σ2, т.е. N(a;σ2), то практически достоверно, что ее значения заключены в интервале (a-3σ; a+3σ). Нарушение данного правила, т.е. отклонение нормально распределенной СВ Х больше, чем на 3σ, является событием практически невозможным, т.к. его вероятность весьма мала: P(|X-a|>3σ) = 1 – P(|X-a|≤3σ) = 1 – 0,9973 = 0,0027.
P(|X-a|>3σ) = 1 – P(|X-a|≤3σ) = 1 – 0,9973 = 0,0027.


