
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность распределения и её свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Закон распределения непрерывной случайной величины удобно задавать с помощью другой функции, называемой плотностью распределения или плотностью вероятности. По определению плотность вероятности f(x) равна первой производной от функции распределения F(x), то есть
Из (*) следует, что F(x) есть первообразная для f(x). Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу, по формуле
При известной плотности распределения f(x) можно найти функцию распределения F(x) по формуле
Плотность вероятности f(x) обладает следующими свойствами: 1. f(x) - неотрицательная функция, то есть
2. Несобственный интеграл от плотности распределения в пределах от -¥ до ¥ равен единице
Если все возможные значения случайной величины принадлежат интервалу (a, b), то последнее равенство можно записать в виде
Определение 1. Модой непрерывной случайной величины Х называется то её значение, при котором плотность распределения максимальна. Моду принято обозначать символом М. На рис. 4 показана мода для непрерывной случайной величины.
Рис. 4.
Если кривая распределения имеет более одного максимума, то распределение называется «полимодальным» (рис. 5).
Рис. 5.
Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом (рис. 6). Такие распределения называются «антимодальными».
Рис. 6. В общем случае мода и математическое ожидание не совпадают. В частном случае, когда распределение является симметричным и модальным (т.е. имеет моду) и существует математическое ожидание, то оно совпадает с модой и центром симметрии распределения. Определение 2. Медианой непрерывной случайной величины Х называется такое её значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е.
Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 7).
Рис. 7.
В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой (рис. 8).
Рис. 8.
Пример 1. Дана функция распределения непрерывной случайной величины Х
Найти f(x). Решение. Так как
Заметим, что при х = 0 производная Пример 2. Дана плотность распределения непрерывной случайной величины Х
Найти F(x). Решение. Воспользуемся формулой (3). Если
Если
Если
Итак, искомая функция распределения имеет вид
Пример 3. Дана плотность распределения непрерывной случайной величины
Найти постоянный параметр С. Решение. Воспользуемся формулой
Потребуем, чтобы это условие выполнялось для заданной функции
Отсюда
Найдем несобственный интеграл
Таким образом, искомый параметр
Пример 4. Дана плотность вероятности непрерывной случайной величины
Найти моду этой случайной величины. Решение. Найдем максимум функции f(x). Для этого определим производные первого и второго порядков:
Из уравнения Значение а в данном случае можно не определять, так как максимум Пример 5. Дана плотность распределения случайной величины Х
Найти медиану этой случайной величины. Решение. Медиану Me найдем из условия
Таким образом, приходим к уравнению
или
Решив биквадратное уравнение, получим
Из четырех корней этого уравнения нужно выбрать тот, который заключен между 0 и 2. Таким образом
Числовые характеристики непрерывных Случайных величин
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством
Предполагается, что (4) сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (a, b), то
Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат Ох, определяется равенством
Если возможные значения Х принадлежат отрезку [a, b], то
Для вычисления дисперсии более удобны формулы
Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для дискретной, равенством
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1051; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

 . (*)
. (*) . (2)
. (2) . (3)
. (3) .
. .
. .
.





 .
.



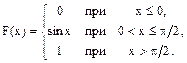
 , то
, то
 не существует.
не существует.
 , то f(x) = 0, следовательно,
, то f(x) = 0, следовательно, .
. , то
, то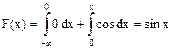 .
. , то
, то .
. .
. .
. .
. . (*)
. (*)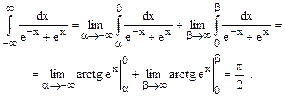
 .
. .
. ,
, .
. находим х = 1. Так как
находим х = 1. Так как  , то при х = 1 функция f(x) имеет максимум, т.е. M = 1.
, то при х = 1 функция f(x) имеет максимум, т.е. M = 1. не зависит от числового значения а.
не зависит от числового значения а.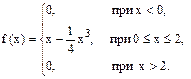
 . В данном случае
. В данном случае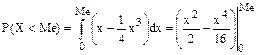 .
. .
.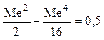
 .
. .
. .
. . (4)
. (4) . (5)
. (5) . (6)
. (6)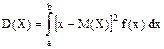 . (7)
. (7) , (6а)
, (6а) . (7а)
. (7а) . (8)
. (8)


